*According to the CBSE Syllabus 2023-24, this chapter has been renumbered as Chapter 12.
The NCERT Solutions for Class 11 Maths Chapter 13 Limits and Derivatives are arranged topic-wise in a systematic manner. The NCERT Solutions are crafted by highly experienced educators in the teaching space, and the solutions for every problem are solved in a simple way, according to the latest update on the CBSE Syllabus 2023-24. These solutions PDF comes in handy for Class 11 students to understand the idea of Limits and Derivatives and to perform well in the CBSE exams.
Download the PDF of NCERT Solutions for Class 11 Maths Chapter 13 – Limits and Derivatives
Access Exercise-wise NCERT Solutions for Class 11 Maths Chapter 13 below
Exercise 13.1 Solutions 32 Questions
Exercise 13.2 Solutions 11 Questions
Miscellaneous Exercise on Chapter 13 Solutions 30 Questions
Access Answers of Maths NCERT Class 11 Chapter 13
Exercise 13.1 page no: 301
1. Evaluate the given limit:
Solution:
Given,
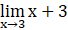
Substituting x = 3, we get
= 3 + 3
= 6
2. Evaluate the given limit:
Solution:
Given limit,
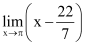
Substituting x = π, we get
 = (π – 22 / 7)
= (π – 22 / 7)
3. Evaluate the given limit:
Solution:
Given limit,
Substituting r = 1, we get
 = π(1)2
= π(1)2
= π
4. Evaluate the given limit:
Solution:
Given limit,
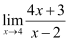
Substituting x = 4, we get
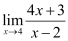 = [4(4) + 3] / (4 – 2)
= [4(4) + 3] / (4 – 2)
= (16 + 3) / 2
= 19 / 2
5. Evaluate the given limit:
Solution:
Given limit,
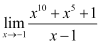
Substituting x = -1, we get
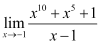
= [(-1)10 + (-1)5 + 1] / (-1 – 1)
= (1 – 1 + 1) / – 2
= – 1 / 2
6. Evaluate the given limit:
Solution:
Given limit,

= [(0 + 1)5 – 1] / 0
=0
Since this limit is undefined,
Substitute x + 1 = y, then x = y – 1

7. Evaluate the given limit:
Solution:

8. Evaluate the given limit:
Solution:

9. Evaluate the given limit:
Solution:

= [a (0) + b] / c (0) + 1
= b / 1
= b
10. Evaluate the given limit: 
Solution:

11. Evaluate the given limit:
Solution:
Given limit,

Substituting x = 1,

= [a (1)2 + b (1) + c] / [c (1)2 + b (1) + a]
= (a + b + c) / (a + b + c)
Given,

= 1
12. Evaluate the given limit:
Solution:
By substituting x = – 2, we get

13. Evaluate the given limit:
Solution:
Given 

14. Evaluate the given limit: 
Solution:

15. Evaluate the given limit:

Solution:

16. Evaluate the given limit:

Solution:

17. Evaluate the given limit:

Solution:


18. Evaluate the given limit:

Solution:

19. Evaluate the given limit:

Solution:

20. Evaluate the given limit:

Solution:


21. Evaluate the given limit:

Solution:


22. Evaluate the given limit:

Solution:


23.

Solution:



24. Find
 , where
, where

Solution:


25. Evaluate
 , where f(x) =
, where f(x) =

Solution:



26. Find
 , where f (x) =
, where f (x) =

Solution:


27. Find
 , where
, where

Solution:


28. Suppose
 and if
and if
 what are the possible values of a and b?
what are the possible values of a and b?
Solution:


29. Let a1, a2,………an be fixed real numbers and define a function
f (x) = (x – a1) (x – a2) ……. (x – an).
What is
 For some a ≠ a1, a2, ……. an, compute
For some a ≠ a1, a2, ……. an, compute
 .
.
Solution:


30. If  For what value (s) of a does
For what value (s) of a does  exist?
exist?
Solution:




31. If the function f(x) satisfies  , evaluate
, evaluate
Solution:


32. If  For what integers m and n does both
For what integers m and n does both  and
and  exist?
exist?
Solution:



Exercise 13.2 page no: 312
1. Find the derivative of x2– 2 at x = 10.
Solution:
Let f (x) = x2 – 2


2. Find the derivative of x at x = 1.
Solution:
Let f (x) = x
Then,


3. Find the derivative of 99x at x = l00.
Solution:
Let f (x) = 99x,
From the first principle,

= 99
4. Find the derivative of the following functions from the first principle.
(i) x3 – 27
(ii) (x – 1) (x – 2)
(iii) 1 / x2
(iv) x + 1 / x – 1
Solution:
(i) Let f (x) = x3 – 27
From the first principle,


(ii) Let f (x) = (x – 1) (x – 2)
From the first principle,


(iii) Let f (x) = 1 / x2
From the first principle, we get


(iv) Let f (x) = x + 1 / x – 1
From the first principle, we get


5. For the function  , prove that f’ (1) =100 f’ (0).
, prove that f’ (1) =100 f’ (0).
Solution:


6. Find the derivative of  for some fixed real number a.
for some fixed real number a.
Solution:

7. For some constants a and b, find the derivative of
(i) (x − a) (x − b)
(ii) (ax2 + b)2
(iii) x – a / x – b
Solution:
(i) (x – a) (x – b)

(ii) (ax2 + b)2

= 4ax (ax2 + b)
(iii) x – a / x – b



8. Find the derivative of  for some constant a.
for some constant a.
Solution:

9. Find the derivative of
(i) 2x – 3 / 4
(ii) (5x3 + 3x – 1) (x – 1)
(iii) x-3 (5 + 3x)
(iv) x5 (3 – 6x-9)
(v) x-4 (3 – 4x-5)
(vi) (2 / x + 1) – x2 / 3x – 1
Solution:
(i)

(ii)

(iii)


(iv)

(v)


(vi)


10. Find the derivative of cos x from the first principle.
Solution:




11. Find the derivative of the following functions.
(i) sin x cos x
(ii) sec x
(iii) 5 sec x + 4 cos x
(iv) cosec x
(v) 3 cot x + 5 cosec x
(vi) 5 sin x – 6 cos x + 7
(vii) 2 tan x – 7 sec x
Solution:
(i) sin x cos x


(ii) sec x



(iii) 5 sec x + 4 cos x

(iv) cosec x



(v) 3 cot x + 5 cosec x








(vi)5 sin x – 6 cos x + 7



(vii) 2 tan x – 7 sec x




Miscellaneous exercise page no: 317
1. Find the derivative of the following functions from the first principle.
(i) –x
(ii) (–x)–1
(iii) sin (x + 1)
(iv) 
Solution:

(ii) (-x)-1





= 1 / x2
(iii) sin (x + 1)



(iv) 

We get,




Find the derivative of the following functions. (It is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants, and m and n are integers.)
2. (x + a)
Solution:

3. (px + q) (r / x + s)
Solution:




4. (ax + b) (cx + d)2
Solution:


5. (ax + b) / (cx + d)
Solution:


6. (1 + 1 / x) / (1 – 1 / x)
Solution:




7. 1 / (ax2 + bx + c)
Solution:


8. (ax + b) / px2 + qx + r
Solution:



9. (px2 + qx + r) / ax + b
Solution:


10. (a / x4) – (b / x2) + cos x
Solution:



11. 
Solution:


12. (ax + b)n
Solution:






13. (ax + b)n (cx + d)m
Solution:





14. sin (x + a)
Solution:




15. cosec x cot x
Solution:


So, we get




16. 
Solution:


17.

Solution:



18.

Solution:



19. sinn x
Solution:





20. 
Solution:


21.

Solution:




22. x4 (5 sin x – 3 cos x)
Solution:


23. (x2 + 1) cos x
Solution:

24. (ax2 + sin x) (p + q cos x)
Solution:

25. 
Solution:



26. 
Solution:


27. 
Solution:

28. 
Solution:





29. (x + sec x) (x – tan x)
Solution:












30. 
Solution:


| Also Access |
| NCERT Exemplar for Class 11 Maths Chapter 13 |
| CBSE Notes for Class 11 Maths Chapter 13 |
NCERT Solutions for Class 11 Maths Chapter 13 – Limits and Derivatives
Class 11 Maths Chapter 13 Limits and Derivatives in the CBSE Syllabus 2023-24 include the following:
13.1 Introduction
This section introduces the branch of Mathematics called calculus, derivative, limits and algebra of limits. Derivatives of certain standard functions are also discussed.
- Calculus is used in electrical engineering to find the length of wire to be used between two stations which are miles apart.
- Calculus is used to find the velocity and trajectory of an object.
- Calculus is used in operations research to improve efficiency and productivity and earn profits.
13.2 Intuitive Idea of Derivatives
This section defines the derivative of a function by giving a real-life example of distance travelled at different intervals of time.
The derivative is the rate of change at which one quantity varies concerning another. If one runs a business (say selling candies), derivatives can help one decide what quantity one should sell. The data on the business performance over the past few months is to be taken, and the trend needs to be analysed by plotting a curve. Derivative defines the instantaneous slope (dy/dx) of this graph.
The slope gives an idea of the marginal cost (change in cost/change in unit produced) of producing every additional unit at that instant. If this cost is greater than 10 bucks, that is the selling price, then a loss is incurred at the point.
For better clarity, refer to the table given below.
For 0-300 units, if the cost > sales, then it’s a loss
For 400-600 units, if the sales > cost, then it’s a profit
13.3 Limits
This section explains limits with an interesting example, left-hand limit and right-hand limit with solved problems.
If an ice cube is dropped into a glass of warm water and the temperature is measured with time, it is an example of a limit as the time approaches infinity. The time measured here is the temperature slowly attaining the room temperature where the glass was stored.
13.3.1 Algebra of limits
This section demonstrates the output of the sum, difference, product and quotient of limits.
13.3.2 Limits of polynomials and rational functions
The limits of polynomials and rational functions are elaborated on, along with solved examples.
13.4 Limits of Trigonometric Functions
This section deals with the theorems and prepositions for functions, which are helpful in calculating the limits of some trigonometric functions.
13.5 Derivatives
This section helps the student to find solutions to different derivative problems.
Money-related establishments need to anticipate the adjustments in the estimation of a specific stock knowing its present worth. In this, and numerous such cases, it is important to know how a specific parameter is changing in accordance with the other parameter. The heart of the text is the derivative of a function at a given point in its domain of definition.
13.5.1 Algebra of derivatives of functions
This section demonstrates the output of the sum, difference, product and quotient of derivatives.
13.5.2 Derivative of polynomials and trigonometric functions
This section deals with the theorems and problems for functions which help calculate the derivatives of some trigonometric functions.
A Few Points on Chapter 13 Limits and Derivatives
- The expected value of the function, as dictated by the points to the left of a point, defines the left-hand limit of the function at that point. Similarly, the right-hand limit.
- The limit of a function at a point is the common value of the left and right-hand limits if they coincide.
- For a function f and a real number, a lim x → a f(x) and f (a) may not be the same.
The solutions given in the PDF contain a definite clarification for each problem. The NCERT Solutions for Class 11 Maths Chapter 13 Limits and Derivatives are accessible at students’ fingertips. The solutions are crafted so that a student will have a comprehension of the marks allotted for every part, which thus benefits them to identify the time they need to allocate to every section of the board exams. High-scoring students have suggested NCERT Solutions to get detailed information on each topic.
Frequently Asked Questions on NCERT Solutions for Class 11 Maths Chapter 13
What is the effective way to study Chapter 13 of NCERT Solutions for Class 11 Maths?
1. Glance at the basic concepts
2. Understand the topic calculus, whether integral or differential
3. Memorise the important formulas
4. Learn limits
5. Learn the fundamental theorem of calculus
6. Practise the problems on a daily basis.
What are the topics included in Chapter 13 of NCERT Solutions for Class 11 Maths?
1. Introduction
2. Intuitive Idea of Derivatives
3. Limits
4. Limits of Trigonometric Functions
5. Derivatives


























































































Comments