The best way to boost the confidence of the students is to practise as many questions as possible. To practise more questions, there is no better resource than the NCERT textbook. Chapter 13 Limits and Derivatives of Class 11 Maths is categorized partly under the CBSE Syllabus for the 2023-24 session. Here is a glance at what the first exercise of Chapter 13 in Class 11 Maths is all about. Exercise 13.1 of NCERT Solutions for Class 11 Maths Chapter 13 – Limits and Derivatives is based on the following topics:
- Introduction to Limits And Derivatives
- Intuitive Idea of Derivatives
- Limits
- Algebra of limits
- Limits of polynomials and rational functions
- Limits of Trigonometric Functions
Downloading and practising the NCERT Solutions of Class 11 Maths will help the students in understanding the concepts covered in Class 11. Once the students attain a good knowledge of the concepts, they would be able to perform effectively in the board examinations.
Download PDF of NCERT Solutions for Class 11 Maths Chapter 13 – Limits and Derivatives Exercise 13.1
Access Other Exercises for Class 11 Maths Chapter 13
Exercise 13.2 Solutions 11 Questions
Miscellaneous Exercise On Chapter 13 Solutions 30 Questions
Also, explore – NCERT Class 11 Solutions
Access Solutions for Class 11 Maths Chapter 13.1 Exercise
1. Evaluate the given limit:
Solution:
Given
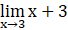
Substituting x = 3, we get
= 3 + 3
= 6
2. Evaluate the given limit:
Solution:
Given limit:
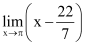
Substituting x = π, we get
 = (π – 22 / 7)
= (π – 22 / 7)
3. Evaluate the given limit:
Solution:
Given limit:
Substituting r = 1, we get
 = π(1)2
= π(1)2
= π
4. Evaluate the given limit:
Solution:
Given limit:
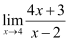
Substituting x = 4, we get
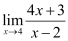 = [4(4) + 3] / (4 – 2)
= [4(4) + 3] / (4 – 2)
= (16 + 3) / 2
= 19 / 2
5. Evaluate the given limit:
Solution:
Given limit:
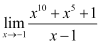
Substituting x = -1, we get
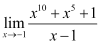
= [(-1)10 + (-1)5 + 1] / (-1 – 1)
= (1 – 1 + 1) / – 2
= – 1 / 2
6. Evaluate the given limit:
Solution:
Given limit:

= [(0 + 1)5 – 1] / 0
=0
Since, this limit is undefined
Substitute x + 1 = y, then x = y – 1

7. Evaluate the given limit:
Solution:

8. Evaluate the given limit:
Solution:

9. Evaluate the given limit:
Solution:

= [a (0) + b] / c (0) + 1
= b / 1
= b
10. Evaluate the given limit: 
Solution:

11. Evaluate the given limit:
Solution:
Given limit:

Substituting x = 1

= [a (1)2 + b (1) + c] / [c (1)2 + b (1) + a]
= (a + b + c) / (a + b + c)
Given

= 1
12. Evaluate the given limit:
Solution:
By substituting x = – 2, we get

13. Evaluate the given limit:
Solution:
Given 

14. Evaluate the given limit: 
Solution:

15. Evaluate the given limit:

Solution:

16. Evaluate the given limit:

Solution:

17. Evaluate the given limit:

Solution:


18. Evaluate the given limit:

Solution:

19. Evaluate the given limit:

Solution:

20. Evaluate the given limit:

Solution:


21. Evaluate the given limit:

Solution:


22. Evaluate the given limit:

Solution:


23.

Solution:



24. Find
 , where
, where

Solution:


25. Evaluate
 , where f(x) =
, where f(x) =

Solution:



26. Find
 , where f (x) =
, where f (x) =

Solution:


27. Find
 , where
, where

Solution:


28. Suppose
 and if
and if
 what are possible values of a and b
what are possible values of a and b
Solution:


29. Let a1, a2,………an be fixed real numbers and define a function
f (x) = (x – a1) (x – a2) ……. (x – an).
What is
 For some a ≠ a1, a2, ……. an, compute
For some a ≠ a1, a2, ……. an, compute

Solution:


30. If  For what value (s) of a does
For what value (s) of a does  exist?
exist?
Solution:




31. If the function f(x) satisfies  , evaluate
, evaluate
Solution:


32. If  For what integers m and n does both
For what integers m and n does both  and
and  exist?
exist?
Solution:

































Comments