RD Sharma Solutions for Class 10 Maths Chapter 5 Trigonometric Ratios Exercise 5.2

Exercise 5.2 of this chapter has problems based on trigonometric ratios of some specific angles like 0, 30, 45, 60 and 90. Expressions are to be evaluated by using the value of these trigonometric ratios. As a student, if you are having difficulty understanding and solving such problems, BYJU’S has created the RD Sharma Solutions Class 10 just for you to give a better experience of learning. For more reference on problems in this exercise, students can download the RD Sharma Solutions for Class 10 Maths Chapter 5 Trigonometric Ratios Exercise 5.2 PDF available below.

RD Sharma Solutions for Class 10 Maths Chapter 5 Trigonometric Ratios Exercise 5.2 Download PDF

Download PDF

carouselExampleControls111

Previous



Next

Access RD Sharma Solutions for Class 10 Maths Chapter 5 Trigonometric Ratios Exercise 5.2

Evaluate each of the following:

1. sin 45^∘ sin 30^∘ + cos 45^∘ cos 30^∘

Solution:

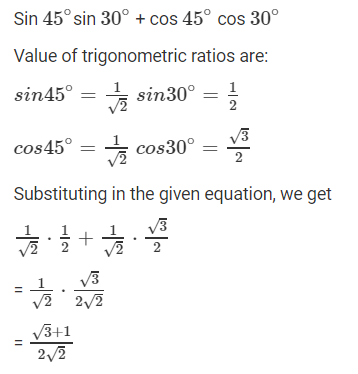
2. sin 60^∘ cos 30^∘ + cos 60^∘ sin 30^∘

Solution:

3.  cos 60^∘ cos 45^∘ – sin 60^∘ sin 45^∘

Solution:

4. sin² 30^∘ + sin² 45^∘ + sin² 60^∘ + sin² 90^∘

Solution:

5.  cos² 30^∘ + cos² 45^∘ + cos² 60^∘ + cos² 90^∘

Solution:

6. tan² 30^∘ + tan² 45^∘ + tan² 60^∘

Solution:

7. 2sin² 30^∘ − 3cos² 45^∘ + tan² 60^∘

Solution:

8. sin² 30^∘ cos²45^∘ + 4tan² 30^∘ + (1/2) sin² 90^∘ − 2cos² 90^∘ + (1/24) cos20^∘

Solution:

9. 4(sin⁴ 60^∘ + cos⁴ 30^∘) − 3(tan² 60^∘ − tan² 45^∘) + 5cos² 45^∘

Solution:

10. (cosec² 45^∘ sec² 30^∘)(sin² 30^∘ + 4cot² 45^∘ − sec² 60^∘)

Solution:

11.  cosec³ 30^∘ cos60^∘ tan³ 45^∘ sin² 90^∘ sec² 45^∘ cot30^∘

Solution:

12. cot² 30^∘ − 2cos² 60^∘ − (3/4)sec² 45^∘ – 4sec² 30^∘

Solution:

Using trigonometric values, we have

13. (cos0^∘ + sin45^∘ + sin30^∘)(sin90^∘ − cos45^∘ + cos60^∘)

Solution:

(cos0^∘ + sin45^∘ + sin30^∘)(sin90^∘ − cos45^∘ + cos60^∘)

Using trigonometric values, we have

15. 4/cot² 30^∘ + 1/sin² 60^∘ − cos² 45^∘

Solution:

16. 4(sin⁴ 30^∘ + cos² 60^∘) − 3(cos² 45^∘ − sin² 90^∘) − sin² 60^∘

Solution:

Using trigonometric values, we have

17.

Solution:

Using trigonometric values, we have

18.

Solution:

Using trigonometric values, we have

19.

Solution:

Using trigonometric values, we have

Find the value of x in each of the following: (20-25)

20. 2sin 3x = √3

Solution:

Given,

2 sin 3x = √3

sin 3x = √3/2

sin 3x = sin 60°

3x = 60°

x = 20°