*According to the CBSE Syllabus 2023-24, this chapter has been renumbered as Chapter 10.
NCERT Solutions for Class 11 Maths Chapter 11 Conic Sections are provided here to enhance the Maths exam preparation of the students and to help them score better marks. Our subject matter experts have developed these NCERT Solutions for Chapter 11 in accordance with the updated syllabus of CBSE Class 11 for 2023-24. Moreover, the solutions have been designed to match the understanding level of the students, so that they can grasp the difficult Maths concepts with ease.
Chapter 11 which is included in the CBSE syllabus aggregates some of the quintessential topics such as Introduction to Conic Sections, Sections of a Circle as well as Circle, Parabola, Hyperbola and Ellipse. So, in order to develop a thorough insight into all these topics, students can rely on NCERT Class 11 Maths Solutions. Using these solutions, the students can practise a more significant number of challenging questions from the chapter to enhance their question-solving skills.
NCERT Solutions for Class 11 Maths Chapter 11 Conic Sections
Access Answers to NCERT Class 11 Maths Chapter 11 – Conic Sections
Access Solutions for Class 11 Maths Chapter 11
EXERCISE 11.1 PAGE NO: 241
In each of the following Exercise 1 to 5, find the equation of the circle with
1. Centre (0, 2) and radius 2
Solution:
Given:
Centre (0, 2) and radius 2
Let us consider the equation of a circle with centre (h, k) and
Radius r is given as (x – h)2 + (y – k)2 = r2
So, centre (h, k) = (0, 2) and radius (r) = 2
The equation of the circle is
(x – 0)2 + (y – 2)2 = 22
x2 + y2 + 4 – 4y = 4
x2 + y2 – 4y = 0
∴ The equation of the circle is x2 + y2 – 4y = 0
2. Centre (–2, 3) and radius 4
Solution:
Given:
Centre (-2, 3) and radius 4
Let us consider the equation of a circle with centre (h, k).
Radius r is given as (x – h)2 + (y – k)2 = r2
So, centre (h, k) = (-2, 3) and radius (r) = 4
The equation of the circle is
(x + 2)2 + (y – 3)2 = (4)2
x2 + 4x + 4 + y2 – 6y + 9 = 16
x2 + y2 + 4x – 6y – 3 = 0
∴ The equation of the circle is x2 + y2 + 4x – 6y – 3 = 0
3. Centre (1/2, 1/4) and radius (1/12)
Solution:
Given:
Centre (1/2, 1/4) and radius 1/12
Let us consider the equation of a circle with centre (h, k).
Radius r is given as (x – h)2 + (y – k)2 = r2
So, centre (h, k) = (1/2, 1/4) and radius (r) = 1/12
The equation of the circle is
(x – 1/2)2 + (y – 1/4)2 = (1/12)2
x2 – x + ¼ + y2 – y/2 + 1/16 = 1/144
x2 – x + ¼ + y2 – y/2 + 1/16 = 1/144
144x2 – 144x + 36 + 144y2 – 72y + 9 – 1 = 0
144x2 – 144x + 144y2 – 72y + 44 = 0
36x2 + 36x + 36y2 – 18y + 11 = 0
36x2 + 36y2 – 36x – 18y + 11= 0
∴ The equation of the circle is 36x2 + 36y2 – 36x – 18y + 11= 0
4. Centre (1, 1) and radius √2
Solution:
Given:
Centre (1, 1) and radius √2
Let us consider the equation of a circle with centre (h, k).
Radius r is given as (x – h)2 + (y – k)2 = r2
So, centre (h, k) = (1, 1) and radius (r) = √2
The equation of the circle is
(x-1)2 + (y-1)2 = (√2)2
x2 – 2x + 1 + y2 -2y + 1 = 2
x2 + y2 – 2x -2y = 0
∴ The equation of the circle is x2 + y2 – 2x -2y = 0
5. Centre (–a, –b) and radius √(a2 – b2)
Solution:
Given:
Centre (-a, -b) and radius √(a2 – b2)
Let us consider the equation of a circle with centre (h, k) and
Radius r is given as (x – h)2 + (y – k)2 = r2
So, centre (h, k) = (-a, -b) and radius (r) = √(a2 – b2)
The equation of the circle is
(x + a)2 + (y + b)2 = (√(a2 – b2)2)
x2 + 2ax + a2 + y2 + 2by + b2 = a2 – b2
x2 + y2 +2ax + 2by + 2b2 = 0
∴ The equation of the circle is x2 + y2 +2ax + 2by + 2b2 = 0
In each of the following Exercise 6 to 9, find the centre and radius of the circles.
6. (x + 5)2 + (y – 3)2 = 36
Solution:
Given:
The equation of the given circle is (x + 5)2 + (y – 3)2 = 36
(x – (-5))2 + (y – 3)2 = 62 [which is of the form (x – h)2 + (y – k )2 = r2]
Where, h = -5, k = 3 and r = 6
∴ The centre of the given circle is (-5, 3) and its radius is 6.
7. x2 + y2 – 4x – 8y – 45 = 0
Solution:
Given:
The equation of the given circle is x2 + y2 – 4x – 8y – 45 = 0.
x2 + y2 – 4x – 8y – 45 = 0
(x2 – 4x) + (y2 -8y) = 45
(x2 – 2(x) (2) + 22) + (y2 – 2(y) (4) + 42) – 4 – 16 = 45
(x – 2)2 + (y – 4)2 = 65
(x – 2)2 + (y – 4)2 = (√65)2 [which is form (x-h)2 +(y-k)2 = r2]
Where h = 2, K = 4 and r = √65
∴ The centre of the given circle is (2, 4) and its radius is √65.
8. x2 + y2 – 8x + 10y – 12 = 0
Solution:
Given:
The equation of the given circle is x2 + y2 -8x + 10y -12 = 0.
x2 + y2 – 8x + 10y – 12 = 0
(x2 – 8x) + (y2 + 10y) = 12
(x2 – 2(x) (4) + 42) + (y2 – 2(y) (5) + 52) – 16 – 25 = 12
(x – 4)2 + (y + 5)2 = 53
(x – 4)2 + (y – (-5))2 = (√53)2 [which is form (x-h)2 +(y-k)2 = r2]
Where h = 4, K= -5 and r = √53
∴ The centre of the given circle is (4, -5) and its radius is √53.
9. 2x2 + 2y2 – x = 0
Solution:
The equation of the given circle is 2x2 + 2y2 –x = 0.
2x2 + 2y2 –x = 0
(2x2 + x) + 2y2 = 0
(x2 – 2 (x) (1/4) + (1/4)2) + y2 – (1/4)2 = 0
(x – 1/4)2 + (y – 0)2 = (1/4)2 [which is form (x-h)2 +(y-k)2 = r2]
Where, h = ¼, K = 0, and r = ¼
∴ The center of the given circle is (1/4, 0) and its radius is 1/4.
10. Find the equation of the circle passing through the points (4,1) and (6,5) and whose centre is on the line 4x + y = 16.
Solution:
Let us consider the equation of the required circle to be (x – h)2+ (y – k)2 = r2
We know that the circle passes through points (4,1) and (6,5)
So,
(4 – h)2 + (1 – k)2 = r2 ……………..(1)
(6– h)2+ (5 – k)2 = r2 ………………(2)
Since, the centre (h, k) of the circle lies on line 4x + y = 16,
4h + k =16………………… (3)
From the equation (1) and (2), we obtain
(4 – h)2+ (1 – k)2 =(6 – h)2 + (5 – k)2
16 – 8h + h2 +1 -2k +k2 = 36 -12h +h2+15 – 10k + k2
16 – 8h +1 -2k + 12h -25 -10k
4h +8k = 44
h + 2k =11……………. (4)
On solving equations (3) and (4), we obtain h=3 and k= 4.
On substituting the values of h and k in equation (1), we obtain
(4 – 3)2+ (1 – 4)2 = r2
(1)2 + (-3)2 = r2
1+9 = r2
r = √10
so now, (x – 3)2 + (y – 4)2 = (√10)2
x2 – 6x + 9 + y2 – 8y + 16 =10
x2 + y2 – 6x – 8y + 15 = 0
∴ The equation of the required circle is x2 + y2 – 6x – 8y + 15 = 0
11. Find the equation of the circle passing through the points (2, 3) and (–1, 1) and whose centre is on the line x – 3y – 11 = 0.
Solution:
Let us consider the equation of the required circle to be (x – h)2 + (y – k)2 = r2
We know that the circle passes through points (2,3) and (-1,1).
(2 – h)2+ (3 – k)2 =r2 ……………..(1)
(-1 – h)2+ (1– k)2 =r2 ………………(2)
Since, the centre (h, k) of the circle lies on line x – 3y – 11= 0,
h – 3k =11………………… (3)
From the equation (1) and (2), we obtain
(2 – h)2+ (3 – k)2 =(-1 – h)2 + (1 – k)2
4 – 4h + h2 +9 -6k +k2 = 1 + 2h +h2+1 – 2k + k2
4 – 4h +9 -6k = 1 + 2h + 1 -2k
6h + 4k =11……………. (4)
Now let us multiply equation (3) by 6 and subtract it from equation (4) to get,
6h+ 4k – 6(h-3k) = 11 – 66
6h + 4k – 6h + 18k = 11 – 66
22 k = – 55
K = -5/2
Substitute this value of K in equation (4) to get,
6h + 4(-5/2) = 11
6h – 10 = 11
6h = 21
h = 21/6
h = 7/2
We obtain h = 7/2and k = -5/2
On substituting the values of h and k in equation (1), we get
(2 – 7/2)2 + (3 + 5/2)2 = r2
[(4-7)/2]2 + [(6+5)/2]2 = r2(-3/2)2 + (11/2)2 = r2
9/4 + 121/4 = r2
130/4 = r2
The equation of the required circle is
(x – 7/2)2 + (y + 5/2)2 = 130/4
[(2x-7)/2]2 + [(2y+5)/2]2 = 130/44x2 -28x + 49 +4y2 + 20y + 25 =130
4x2 +4y2 -28x + 20y – 56 = 0
4(x2 +y2 -7x + 5y – 14) = 0
x2 + y2 – 7x + 5y – 14 = 0
∴ The equation of the required circle is x2 + y2 – 7x + 5y – 14 = 0
12. Find the equation of the circle with radius 5 whose centre lies on x-axis and passes through the point (2, 3).
Solution:
Let us consider the equation of the required circle to be (x – h)2+ (y – k)2 = r2
We know that the radius of the circle is 5 and its centre lies on the x-axis, k = 0 and r = 5.
So now, the equation of the circle is (x – h)2 + y2 = 25.
It is given that the circle passes through the point (2, 3) so the point will satisfy the equation of the circle.
(2 – h)2+ 32 = 25
(2 – h)2 = 25-9
(2 – h)2 = 16
2 – h = ± √16 = ± 4
If 2-h = 4, then h = -2
If 2-h = -4, then h = 6
Then, when h = -2, the equation of the circle becomes
(x + 2)2 + y2 = 25
x2 + 12x + 36 + y2 = 25
x2 + y2 + 4x – 21 = 0
When h = 6, the equation of the circle becomes
(x – 6)2 + y2 = 25
x2 -12x + 36 + y2 = 25
x2 + y2 -12x + 11 = 0
∴ The equation of the required circle is x2 + y2 + 4x – 21 = 0 and x2 + y2 -12x + 11 = 0
13. Find the equation of the circle passing through (0,0) and making intercepts a and b on the coordinate axes.
Solution:
Let us consider the equation of the required circle to be (x – h)2+ (y – k)2 =r2
We know that the circle passes through (0, 0),
So, (0 – h)2+ (0 – k)2 = r2
h2 + k2 = r2
Now, The equation of the circle is (x – h)2 + (y – k)2 = h2 + k2.
It is given that the circle intercepts a and b on the coordinate axes.
i.e., the circle passes through points (a, 0) and (0, b).
So, (a – h)2+ (0 – k)2 =h2 +k2……………..(1)
(0 – h)2+ (b– k)2 =h2 +k2………………(2)
From equation (1), we obtain
a2 – 2ah + h2 +k2 = h2 +k2
a2 – 2ah = 0
a(a – 2h) =0
a = 0 or (a -2h) = 0
However, a ≠ 0; hence, (a -2h) = 0
h = a/2
From equation (2), we obtain
h2 – 2bk + k2 + b2= h2 +k2
b2 – 2bk = 0
b(b– 2k) = 0
b= 0 or (b-2k) =0
However, a ≠ 0; hence, (b -2k) = 0
k =b/2
So, the equation is
(x – a/2)2 + (y – b/2)2 = (a/2)2 + (b/2)2
[(2x-a)/2]2 + [(2y-b)/2]2 = (a2 + b2)/44x2 – 4ax + a2 +4y2 – 4by + b2 = a2 + b2
4x2 + 4y2 -4ax – 4by = 0
4(x2 +y2 -7x + 5y – 14) = 0
x2 + y2 – ax – by = 0
∴ The equation of the required circle is x2 + y2 – ax – by = 0
14. Find the equation of a circle with centre (2,2) and passes through the point (4,5).
Solution:
Given:
The centre of the circle is given as (h, k) = (2,2)
We know that the circle passes through point (4,5), the radius (r) of the circle is the distance between the points (2,2) and (4,5).
r = √[(2-4)2 + (2-5)2]
= √[(-2)2 + (-3)2]
= √[4+9]
= √13
The equation of the circle is given as
(x– h)2+ (y – k)2 = r2
(x –h)2 + (y – k)2 = (√13)2
(x –2)2 + (y – 2)2 = (√13)2
x2 – 4x + 4 + y2 – 4y + 4 = 13
x2 + y2 – 4x – 4y = 5
∴ The equation of the required circle is x2 + y2 – 4x – 4y = 5
15. Does the point (–2.5, 3.5) lie inside, outside or on the circle x2 + y2 = 25?
Solution:
Given:
The equation of the given circle is x2 +y2 = 25.
x2 + y2 = 25
(x – 0)2 + (y – 0)2 = 52 [which is of the form (x – h)2 + (y – k)2 = r2]
Where, h = 0, k = 0 and r = 5.
So the distance between point (-2.5, 3.5) and the centre (0,0) is
= √[(-2.5 – 0)2 + (-3.5 – 0)2]
= √(6.25 + 12.25)
= √18.5
= 4.3 [which is < 5]
Since, the distance between point (-2.5, -3.5) and the centre (0, 0) of the circle is less than the radius of the circle, point (-2.5, -3.5) lies inside the circle.
EXERCISE 11.2 PAGE NO: 246
In each of the following Exercises 1 to 6, find the coordinates of the focus, axis of the parabola, the equation of the directrix and the length of the latus rectum.
1. y2 = 12x
Solution:
Given:
The equation is y2 = 12x
Here, we know that the coefficient of x is positive.
So, the parabola opens towards the right.
On comparing this equation with y2 = 4ax, we get,
4a = 12
a = 3
Thus, the co-ordinates of the focus = (a, 0) = (3, 0)
Since the given equation involves y2, the axis of the parabola is the x-axis.
∴ The equation of directrix, x = -a, then,
x + 3 = 0
Length of latus rectum = 4a = 4 × 3 = 12
2. x2 = 6y
Solution:
Given:
The equation is x2 = 6y
Here, we know that the coefficient of y is positive.
So, the parabola opens upwards.
On comparing this equation with x2 = 4ay, we get,
4a = 6
a = 6/4
= 3/2
Thus, the co-ordinates of the focus = (0,a) = (0, 3/2)
Since the given equation involves x2, the axis of the parabola is the y-axis.
∴ The equation of directrix, y =-a, then,
y = -3/2
Length of latus rectum = 4a = 4(3/2) = 6
3. y2 = – 8x
Solution:
Given:
The equation is y2 = -8x
Here, we know that the coefficient of x is negative.
So, the parabola open towards the left.
On comparing this equation with y2 = -4ax, we get,
-4a = -8
a = -8/-4 = 2
Thus, co-ordinates of the focus = (-a,0) = (-2, 0)
Since the given equation involves y2, the axis of the parabola is the x-axis.
∴ Equation of directrix, x =a, then,
x = 2
Length of latus rectum = 4a = 4 (2) = 8
4. x2 = – 16y
Solution:
Given:
The equation is x2 = -16y
Here, we know that the coefficient of y is negative.
So, the parabola opens downwards.
On comparing this equation with x2 = -4ay, we get,
-4a = -16
a = -16/-4
= 4
Thus, co-ordinates of the focus = (0,-a) = (0,-4)
Since the given equation involves x2, the axis of the parabola is the y-axis.
∴ The equation of directrix, y =a, then,
y = 4
Length of latus rectum = 4a = 4(4) = 16
5. y2 = 10x
Solution:
Given:
The equation is y2 = 10x
Here, we know that the coefficient of x is positive.
So, the parabola open towards the right.
On comparing this equation with y2 = 4ax, we get,
4a = 10
a = 10/4 = 5/2
Thus, co-ordinates of the focus = (a,0) = (5/2, 0)
Since the given equation involves y2, the axis of the parabola is the x-axis.
∴ The equation of directrix, x =-a, then,
x = – 5/2
Length of latus rectum = 4a = 4(5/2) = 10
6. x2 = – 9y
Solution:
Given:
The equation is x2 = -9y
Here, we know that the coefficient of y is negative.
So, the parabola open downwards.
On comparing this equation with x2 = -4ay, we get,
-4a = -9
a = -9/-4 = 9/4
Thus, co-ordinates of the focus = (0,-a) = (0, -9/4)
Since the given equation involves x2, the axis of the parabola is the y-axis.
∴ The equation of directrix, y = a, then,
y = 9/4
Length of latus rectum = 4a = 4(9/4) = 9
In each of the Exercises 7 to 12, find the equation of the parabola that satisfies the given conditions:
7. Focus (6,0); directrix x = – 6
Solution:
Given:
Focus (6,0) and directrix x = -6
We know that the focus lies on the x–axis is the axis of the parabola.
So, the equation of the parabola is either of the form y2 = 4ax or y2 = -4ax.
It is also seen that the directrix, x = -6 is to the left of the y- axis,
While the focus (6, 0) is to the right of the y –axis.
Hence, the parabola is of the form y2 = 4ax.
Here, a = 6
∴ The equation of the parabola is y2 = 24x.
8. Focus (0,–3); directrix y = 3
Solution:
Given:
Focus (0, -3) and directrix y = 3
We know that the focus lies on the y–axis, the y-axis is the axis of the parabola.
So, the equation of the parabola is either of the form x2 = 4ay or x2 = -4ay.
It is also seen that the directrix, y = 3 is above the x- axis,
While the focus (0,-3) is below the x-axis.
Hence, the parabola is of the form x2 = -4ay.
Here, a = 3
∴ The equation of the parabola is x2 = -12y.
9. Vertex (0, 0); focus (3, 0)
Solution:
Given:
Vertex (0, 0) and focus (3, 0)
We know that the vertex of the parabola is (0, 0) and the focus lies on the positive x-axis. [x-axis is the axis of the parabola.]
The equation of the parabola is of the form y2 = 4ax.
Since, the focus is (3, 0), a = 3
∴ The equation of the parabola is y2 = 4 × 3 × x,
y2 = 12x
10. Vertex (0, 0); focus (–2, 0)
Solution:
Given:
Vertex (0, 0) and focus (-2, 0)
We know that the vertex of the parabola is (0, 0) and the focus lies on the positive x-axis. [x-axis is the axis of the parabola.]
The equation of the parabola is of the form y2=-4ax.
Since, the focus is (-2, 0), a = 2
∴ The equation of the parabola is y2 = -4 × 2 × x,
y2 = -8x
11. Vertex (0, 0) passing through (2, 3) and axis is along x-axis.
Solution:
We know that the vertex is (0, 0) and the axis of the parabola is the x-axis
The equation of the parabola is either of the form y2 = 4ax or y2 = -4ax.
Given that the parabola passes through point (2, 3), which lies in the first quadrant.
So, the equation of the parabola is of the form y2 = 4ax, while point (2, 3) must satisfy the equation y2 = 4ax.
Then,
32 = 4a(2)
32 = 8a
9 = 8a
a = 9/8
Thus, the equation of the parabola is
y2 = 4 (9/8)x
= 9x/2
2y2 = 9x
∴ The equation of the parabola is 2y2 = 9x
12. Vertex (0, 0), passing through (5, 2) and symmetric with respect to y-axis.
Solution:
We know that the vertex is (0, 0) and the parabola is symmetric about the y-axis.
The equation of the parabola is either of the form x2 = 4ay or x2 = -4ay.
Given that the parabola passes through point (5, 2), which lies in the first quadrant.
So, the equation of the parabola is of the form x2 = 4ay, while point (5, 2) must satisfy the equation x2 = 4ay.
Then,
52 = 4a(2)
25 = 8a
a = 25/8
Thus, the equation of the parabola is
x2 = 4 (25/8)y
x2 = 25y/2
2x2 = 25y
∴ The equation of the parabola is 2x2 = 25y
EXERCISE 11.3 PAGE NO: 255
In each of the Exercises 1 to 9, find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.
1. x2/36 + y2/16 = 1
Solution:
Given:
The equation is x2/36 + y2/16 = 1
Here, the denominator of x2/36 is greater than the denominator of y2/16.
So, the major axis is along the x-axis, while the minor axis is along the y-axis.
On comparing the given equation with x2/a2 + y2/b2 = 1, we get
a = 6 and b = 4.
c = √(a2 – b2)
= √(36-16)
= √20
= 2√5
Then,
The coordinates of the foci are (2√5, 0) and (-2√5, 0).
The coordinates of the vertices are (6, 0) and (-6, 0)
Length of major axis = 2a = 2 (6) = 12
Length of minor axis = 2b = 2 (4) = 8
Eccentricity, e = c/a = 2√5/6 = √5/3
Length of latus rectum = 2b2/a = (2×16)/6 = 16/3
2. x2/4 + y2/25 = 1
Solution:
Given:
The equation is x2/4 + y2/25 = 1
Here, the denominator of y2/25 is greater than the denominator of x2/4.
So, the major axis is along the x-axis, while the minor axis is along the y-axis.
On comparing the given equation with x2/a2 + y2/b2 = 1, we get
a = 5 and b = 2.
c = √(a2 – b2)
= √(25-4)
= √21
Then,
The coordinates of the foci are (0, √21) and (0, -√21).
The coordinates of the vertices are (0, 5) and (0, -5)
Length of the major axis = 2a = 2 (5) = 10
Length of the minor axis = 2b = 2 (2) = 4
Eccentricity, e = c/a = √21/5
Length of latus rectum = 2b2/a = (2×22)/5 = (2×4)/5 = 8/5
3. x2/16 + y2/9 = 1
Solution:
Given:
The equation is x2/16 + y2/9 = 1 or x2/42 + y2/32 = 1
Here, the denominator of x2/16 is greater than the denominator of y2/9.
So, the major axis is along the x-axis, while the minor axis is along the y-axis.
On comparing the given equation with x2/a2 + y2/b2 = 1, we get
a = 4 and b = 3.
c = √(a2 – b2)
= √(16-9)
= √7
Then,
The coordinates of the foci are (√7, 0) and (-√7, 0).
The coordinates of the vertices are (4, 0) and (-4, 0)
Length of the major axis = 2a = 2 (4) = 8
Length of the minor axis = 2b = 2 (3) = 6
Eccentricity, e = c/a = √7/4
Length of latus rectum = 2b2/a = (2×32)/4 = (2×9)/4 = 18/4 = 9/2
4. x2/25 + y2/100 = 1
Solution:
Given:
The equation is x2/25 + y2/100 = 1
Here, the denominator of y2/100 is greater than the denominator of x2/25.
So, the major axis is along the y-axis, while the minor axis is along the x-axis.
On comparing the given equation with x2/b2 + y2/a2 = 1, we get
b = 5 and a =10.
c = √(a2 – b2)
= √(100-25)
= √75
= 5√3
Then,
The coordinates of the foci are (0, 5√3) and (0, -5√3).
The coordinates of the vertices are (0, √10) and (0, -√10)
Length of the major axis = 2a = 2 (10) = 20
Length of the minor axis = 2b = 2 (5) = 10
Eccentricity, e = c/a = 5√3/10 = √3/2
Length of latus rectum = 2b2/a = (2×52)/10 = (2×25)/10 = 5
5. x2/49 + y2/36 = 1
Solution:
Given:
The equation is x2/49 + y2/36 = 1
Here, the denominator of x2/49 is greater than the denominator of y2/36.
So, the major axis is along the x-axis, while the minor axis is along the y-axis.
On comparing the given equation with x2/a2 + y2/b2 = 1, we get
b = 6 and a =7
c = √(a2 – b2)
= √(49-36)
= √13
Then,
The coordinates of the foci are (√13, 0) and (-√3, 0).
The coordinates of the vertices are (7, 0) and (-7, 0)
Length of the major axis = 2a = 2 (7) = 14
Length of the minor axis = 2b = 2 (6) = 12
Eccentricity, e = c/a = √13/7
Length of latus rectum = 2b2/a = (2×62)/7 = (2×36)/7 = 72/7
6. x2/100 + y2/400 = 1
Solution:
Given:
The equation is x2/100 + y2/400 = 1
Here, the denominator of y2/400 is greater than the denominator of x2/100.
So, the major axis is along the y-axis, while the minor axis is along the x-axis.
On comparing the given equation with x2/b2 + y2/a2 = 1, we get
b = 10 and a =20.
c = √(a2 – b2)
= √(400-100)
= √300
= 10√3
Then,
The coordinates of the foci are (0, 10√3) and (0, -10√3).
The coordinates of the vertices are (0, 20) and (0, -20)
Length of the major axis = 2a = 2 (20) = 40
Length of the minor axis = 2b = 2 (10) = 20
Eccentricity, e = c/a = 10√3/20 = √3/2
Length of latus rectum = 2b2/a = (2×102)/20 = (2×100)/20 = 10
7. 36x2 + 4y2 = 144
Solution:
Given:
The equation is 36x2 + 4y2 = 144 or x2/4 + y2/36 = 1 or x2/22 + y2/62 = 1
Here, the denominator of y2/62 is greater than the denominator of x2/22.
So, the major axis is along the y-axis, while the minor axis is along the x-axis.
On comparing the given equation with x2/b2 + y2/a2 = 1, we get
b = 2 and a = 6.
c = √(a2 – b2)
= √(36-4)
= √32
= 4√2
Then,
The coordinates of the foci are (0, 4√2) and (0, -4√2).
The coordinates of the vertices are (0, 6) and (0, -6)
Length of the major axis = 2a = 2 (6) = 12
Length of the minor axis = 2b = 2 (2) = 4
Eccentricity, e = c/a = 4√2/6 = 2√2/3
Length of latus rectum = 2b2/a = (2×22)/6 = (2×4)/6 = 4/3
8. 16x2 + y2 = 16
Solution:
Given:
The equation is 16x2 + y2 = 16 or x2/1 + y2/16 = 1 or x2/12 + y2/42 = 1
Here, the denominator of y2/42 is greater than the denominator of x2/12.
So, the major axis is along the y-axis, while the minor axis is along the x-axis.
On comparing the given equation with x2/b2 + y2/a2 = 1, we get
b =1 and a =4.
c = √(a2 – b2)
= √(16-1)
= √15
Then,
The coordinates of the foci are (0, √15) and (0, -√15).
The coordinates of the vertices are (0, 4) and (0, -4)
Length of the major axis = 2a = 2 (4) = 8
Length of the minor axis = 2b = 2 (1) = 2
Eccentricity, e = c/a = √15/4
Length of latus rectum = 2b2/a = (2×12)/4 = 2/4 = ½
9. 4x2 + 9y2 = 36
Solution:
Given:
The equation is 4x2 + 9y2 = 36 or x2/9 + y2/4 = 1 or x2/32 + y2/22 = 1
Here, the denominator of x2/32 is greater than the denominator of y2/22.
So, the major axis is along the x-axis, while the minor axis is along the y-axis.
On comparing the given equation with x2/a2 + y2/b2 = 1, we get
a =3 and b =2.
c = √(a2 – b2)
= √(9-4)
= √5
Then,
The coordinates of the foci are (√5, 0) and (-√5, 0).
The coordinates of the vertices are (3, 0) and (-3, 0)
Length of the major axis = 2a = 2 (3) = 6
Length of the minor axis = 2b = 2 (2) = 4
Eccentricity, e = c/a = √5/3
Length of latus rectum = 2b2/a = (2×22)/3 = (2×4)/3 = 8/3
In each of the following Exercises 10 to 20, find the equation for the ellipse that satisfies the given conditions:
10. Vertices (± 5, 0), foci (± 4, 0)
Solution:
Given:
Vertices (± 5, 0) and foci (± 4, 0)
Here, the vertices are on the x-axis.
So, the equation of the ellipse will be of the form x2/a2 + y2/b2 = 1, where ‘a’ is the semi-major axis.
Then, a = 5 and c = 4.
It is known that a2 = b2 + c2.
So, 52 = b2 + 42
25 = b2 + 16
b2 = 25 – 16
b = √9
= 3
∴ The equation of the ellipse is x2/52 + y2/32 = 1 or x2/25 + y2/9 = 1
11. Vertices (0, ± 13), foci (0, ± 5)
Solution:
Given:
Vertices (0, ± 13) and foci (0, ± 5)
Here, the vertices are on the y-axis.
So, the equation of the ellipse will be of the form x2/b2 + y2/a2 = 1, where ‘a’ is the semi-major axis.
Then, a =13 and c = 5.
It is known that a2 = b2 + c2.
132 = b2+52
169 = b2 + 15
b2 = 169 – 125
b = √144
= 12
∴ The equation of the ellipse is x2/122 + y2/132 = 1 or x2/144 + y2/169 = 1
12. Vertices (± 6, 0), foci (± 4, 0)
Solution:
Given:
Vertices (± 6, 0) and foci (± 4, 0)
Here, the vertices are on the x-axis.
So, the equation of the ellipse will be of the form x2/a2 + y2/b2 = 1, where ‘a’ is the semi-major axis.
Then, a = 6 and c = 4.
It is known that a2 = b2 + c2.
62 = b2+42
36 = b2 + 16
b2 = 36 – 16
b = √20
∴ The equation of the ellipse is x2/62 + y2/(√20)2 = 1 or x2/36 + y2/20 = 1
13. Ends of major axis (± 3, 0), ends of minor axis (0, ±2)
Solution:
Given:
Ends of major axis (± 3, 0) and ends of minor axis (0, ±2)
Here, the major axis is along the x-axis.
So, the equation of the ellipse will be of the form x2/a2 + y2/b2 = 1, where ‘a’ is the semi-major axis.
Then, a = 3 and b = 2.
∴ The equation for the ellipse x2/32 + y2/22 = 1 or x2/9 + y2/4 = 1
14. Ends of major axis (0, ±√5), ends of minor axis (±1, 0)
Solution:
Given:
Ends of major axis (0, ±√5) and ends of minor axis (±1, 0)
Here, the major axis is along the y-axis.
So, the equation of the ellipse will be of the form x2/b2 + y2/a2 = 1, where ‘a’ is the semi-major axis.
Then, a = √5 and b = 1.
∴ The equation for the ellipse x2/12 + y2/(√5)2 = 1 or x2/1 + y2/5 = 1
15. Length of major axis 26, foci (±5, 0)
Solution:
Given:
Length of major axis is 26 and foci (±5, 0)
Since the foci are on the x-axis, the major axis is along the x-axis.
So, the equation of the ellipse will be of the form x2/a2 + y2/b2 = 1, where ‘a’ is the semi-major axis.
Then, 2a = 26
a = 13 and c = 5.
It is known that a2 = b2 + c2.
132 = b2+52
169 = b2 + 25
b2 = 169 – 25
b = √144
= 12
∴ The equation of the ellipse is x2/132 + y2/122 = 1 or x2/169 + y2/144 = 1
16. Length of minor axis 16, foci (0, ±6).
Solution:
Given:
Length of minor axis is 16 and foci (0, ±6).
Since the foci are on the y-axis, the major axis is along the y-axis.
So, the equation of the ellipse will be of the form x2/b2 + y2/a2 = 1, where ‘a’ is the semi-major axis.
Then, 2b =16
b = 8 and c = 6.
It is known that a2 = b2 + c2.
a2 = 82 + 62
= 64 + 36
=100
a = √100
= 10
∴ The equation of the ellipse is x2/82 + y2/102 =1 or x2/64 + y2/100 = 1
17. Foci (±3, 0), a = 4
Solution:
Given:
Foci (±3, 0) and a = 4
Since the foci are on the x-axis, the major axis is along the x-axis.
So, the equation of the ellipse will be of the form x2/a2 + y2/b2 = 1, where ‘a’ is the semi-major axis.
Then, c = 3 and a = 4.
It is known that a2 = b2 + c2.
a2 = 82 + 62
= 64 + 36
= 100
16 = b2 + 9
b2 = 16 – 9
= 7
∴ The equation of the ellipse is x2/16 + y2/7 = 1
18. b = 3, c = 4, centre at the origin; foci on the x axis.
Solution:
Given:
b = 3, c = 4, centre at the origin and foci on the x axis.
Since the foci are on the x-axis, the major axis is along the x-axis.
So, the equation of the ellipse will be of the form x2/a2 + y2/b2 = 1, where ‘a’ is the semi-major axis.
Then, b = 3 and c = 4.
It is known that a2 = b2 + c2.
a2 = 32 + 42
= 9 + 16
=25
a = √25
= 5
∴ The equation of the ellipse is x2/52 + y2/32 or x2/25 + y2/9 = 1
19. Centre at (0, 0), major axis on the y-axis and passes through the points (3, 2) and (1, 6).
Solution:
Given:
Centre at (0, 0), major axis on the y-axis and passes through the points (3, 2) and (1, 6).
Since the centre is at (0, 0) and the major axis is on the y- axis, the equation of the ellipse will be of the form x2/b2 + y2/a2 = 1, where ‘a’ is the semi-major axis.
The ellipse passes through points (3, 2) and (1, 6).
So, by putting the values x = 3 and y = 2, we get,
32/b2 + 22/a2 = 1
9/b2 + 4/a2…. (1)
And by putting the values x = 1 and y = 6, we get,
11/b2 + 62/a2 = 1
1/b2 + 36/a2 = 1 …. (2)
On solving equation (1) and (2), we get
b2 = 10 and a2 = 40.
∴ The equation of the ellipse is x2/10 + y2/40 = 1 or 4x2 + y 2 = 40
20. Major axis on the x-axis and passes through the points (4,3) and (6,2).
Solution:
Given:
Major axis on the x-axis and passes through the points (4, 3) and (6, 2).
Since the major axis is on the x-axis, the equation of the ellipse will be the form
x2/a2 + y2/b2 = 1…. (1) [Where ‘a’ is the semi-major axis.]
The ellipse passes through points (4, 3) and (6, 2).
So by putting the values x = 4 and y = 3 in equation (1), we get,
16/a2 + 9/b2 = 1 …. (2)
Putting, x = 6 and y = 2 in equation (1), we get,
36/a2 + 4/b2 = 1 …. (3)
From equation (2)
16/a2 = 1 – 9/b2
1/a2 = (1/16 (1 – 9/b2)) …. (4)
Substituting the value of 1/a2 in equation (3) we get,
36/a2 + 4/b2 = 1
36(1/a2) + 4/b2 = 1
36[1/16 (1 – 9/b2)] + 4/b2 = 1
36/16 (1 – 9/b2) + 4/b2 = 1
9/4 (1 – 9/b2) + 4/b2 = 1
9/4 – 81/4b2 + 4/b2 = 1
-81/4b2 + 4/b2 = 1 – 9/4
(-81+16)/4b2 = (4-9)/4
-65/4b2 = -5/4
-5/4(13/b2) = -5/4
13/b2 = 1
1/b2 = 1/13
b2 = 13
Now substituting the value of b2 in equation (4) we get,
1/a2 = 1/16(1 – 9/b2)
= 1/16(1 – 9/13)
= 1/16((13-9)/13)
= 1/16(4/13)
= 1/52
a2 = 52
Equation of ellipse is x2/a2 + y2/b2 = 1
By substituting the values of a2 and b2 in above equation we get,
x2/52 + y2/13 = 1
EXERCISE 11.4 PAGE NO: 262
In each of the Exercises 1 to 6, find the coordinates of the foci and the vertices, the eccentricity and the length of the latus rectum of the hyperbolas.
1. x2/16 – y2/9 = 1
Solution:
Given:
The equation is x2/16 – y2/9 = 1 or x2/42 – y2/32 = 1
On comparing this equation with the standard equation of hyperbola x2/a2 – y2/b2 = 1,
We get a = 4 and b = 3,
It is known that a2 + b2 = c2
So,
c2 = 42 + 32
= √25
c = 5
Then,
The coordinates of the foci are (±5, 0).
The coordinates of the vertices are (±4, 0).
Eccentricity, e = c/a = 5/4
Length of latus rectum = 2b2/a = (2 × 32)/4 = (2×9)/4 = 18/4 = 9/2
2. y2/9 – x2/27 = 1
Solution:
Given:
The equation is y2/9 – x2/27 = 1 or y2/32 – x2/272 = 1
On comparing this equation with the standard equation of hyperbola y2/a2 – x2/b2 = 1,
We get a = 3 and b = √27,
It is known that a2 + b2 = c2
So,
c2 = 32 + (√27)2
= 9 + 27
c2 = 36
c = √36
= 6
Then,
The coordinates of the foci are (0, 6) and (0, -6).
The coordinates of the vertices are (0, 3) and (0, – 3).
Eccentricity, e = c/a = 6/3 = 2
Length of latus rectum = 2b2/a = (2 × 27)/3 = (54)/3 = 18
3. 9y2 – 4x2 = 36
Solution:
Given:
The equation is 9y2 – 4x2 = 36 or y2/4 – x2/9 = 1 or y2/22 – x2/32 = 1
On comparing this equation with the standard equation of hyperbola y2/a2 – x2/b2 = 1,
We get a = 2 and b = 3,
It is known that a2 + b2 = c2
So,
c2 = 4 + 9
c2 = 13
c = √13
Then,
The coordinates of the foci are (0, √13) and (0, –√13).
The coordinates of the vertices are (0, 2) and (0, – 2).
Eccentricity, e = c/a = √13/2
Length of latus rectum = 2b2/a = (2 × 32)/2 = (2×9)/2 = 18/2 = 9
4. 16x2 – 9y2 = 576
Solution:
Given:
The equation is 16x2 – 9y2 = 576
Let us divide the whole equation by 576.We get
16x2/576 – 9y2/576 = 576/576
x2/36 – y2/64 = 1
On comparing this equation with the standard equation of hyperbola x2/a2 – y2/b2 = 1,
We get a = 6 and b = 8,
It is known that a2 + b2 = c2
So,
c2 = 36 + 64
c2 = √100
c = 10
Then,
The coordinates of the foci are (10, 0) and (-10, 0).
The coordinates of the vertices are (6, 0) and (-6, 0).
Eccentricity, e = c/a = 10/6 = 5/3
Length of latus rectum = 2b2/a = (2 × 82)/6 = (2×64)/6 = 64/3
5. 5y2 – 9x2 = 36
Solution:
Given:
The equation is 5y2 – 9x2 = 36
Let us divide the whole equation by 36. We get
5y2/36 – 9x2/36 = 36/36
y2/(36/5) – x2/4 = 1
On comparing this equation with the standard equation of hyperbola y2/a2 – x2/b2 = 1,
We get a = 6/√5 and b = 2,
It is known that a2 + b2 = c2
So,
c2 = 36/5 + 4
c2 = 56/5
c = √(56/5)
= 2√14/√5
Then,
The coordinates of the foci are (0, 2√14/√5) and (0, – 2√14/√5).
The coordinates of the vertices are (0, 6/√5) and (0, -6/√5).
Eccentricity, e = c/a = (2√14/√5) / (6/√5) = √14/3
Length of latus rectum = 2b2/a = (2 × 22)/6/√5 = (2×4)/6/√5 = 4√5/3
6. 49y2 – 16x2 = 784.
Solution:
Given:
The equation is 49y2 – 16x2 = 784.
Let us divide the whole equation by 784, we get
49y2/784 – 16x2/784 = 784/784
y2/16 – x2/49 = 1
On comparing this equation with the standard equation of hyperbola y2/a2 – x2/b2 = 1,
We get a = 4 and b = 7,
It is known that a2 + b2 = c2
So,
c2 = 16 + 49
c2 = 65
c = √65
Then,
The coordinates of the foci are (0, √65) and (0, –√65).
The coordinates of the vertices are (0, 4) and (0, -4).
Eccentricity, e = c/a = √65/4
Length of latus rectum = 2b2/a = (2 × 72)/4 = (2×49)/4 = 49/2
In each Exercises 7 to 15, find the equations of the hyperbola satisfying the given conditions
7. Vertices (±2, 0), foci (±3, 0)
Solution:
Given:
Vertices (±2, 0) and foci (±3, 0)
Here, the vertices are on the x-axis.
So, the equation of the hyperbola is of the form x2/a2 – y2/b2 = 1
Since the vertices are (±2, 0), so, a = 2
Since the foci are (±3, 0), so, c = 3
It is known that, a2 + b2 = c2
So, 22 + b2 = 32
b2 = 9 – 4 = 5
∴ The equation of the hyperbola is x2/4 – y2/5 = 1
8. Vertices (0, ± 5), foci (0, ± 8)
Solution:
Given:
Vertices (0, ± 5) and foci (0, ± 8)
Here, the vertices are on the y-axis.
So, the equation of the hyperbola is of the form y2/a2 – x2/b2 = 1
Since the vertices are (0, ±5), so, a = 5
Since the foci are (0, ±8), so, c = 8
It is known that, a2 + b2 = c2
So, 52 + b2 = 82
b2 = 64 – 25 = 39
∴ The equation of the hyperbola is y2/25 – x2/39 = 1
9. Vertices (0, ± 3), foci (0, ± 5)
Solution:
Given:
Vertices (0, ± 3) and foci (0, ± 5)
Here, the vertices are on the y-axis.
So, the equation of the hyperbola is of the form y2/a2 – x2/b2 = 1
Since the vertices are (0, ±3), so, a = 3
Since the foci are (0, ±5), so, c = 5
It is known that a2 + b2 = c2
So, 32 + b2 = 52
b2 = 25 – 9 = 16
∴ The equation of the hyperbola is y2/9 – x2/16 = 1
10. Foci (±5, 0), the transverse axis is of length 8.
Solution:
Given:
Foci (±5, 0) and the transverse axis is of length 8.
Here, the foci are on x-axis.
The equation of the hyperbola is of the form x2/a2 – y2/b2 = 1
Since the foci are (±5, 0), so, c = 5
Since the length of the transverse axis is 8,
2a = 8
a = 8/2
= 4
It is known that a2 + b2 = c2
42 + b2 = 52
b2 = 25 – 16
= 9
∴ The equation of the hyperbola is x2/16 – y2/9 = 1
11. Foci (0, ±13), the conjugate axis is of length 24.
Solution:
Given:
Foci (0, ±13) and the conjugate axis is of length 24.
Here, the foci are on y-axis.
The equation of the hyperbola is of the form y2/a2 – x2/b2 = 1
Since the foci are (0, ±13), so, c = 13
Since the length of the conjugate axis is 24,
2b = 24
b = 24/2
= 12
It is known that a2 + b2 = c2
a2 + 122 = 132
a2 = 169 – 144
= 25
∴ The equation of the hyperbola is y2/25 – x2/144 = 1
12. Foci (± 3√5, 0), the latus rectum is of length 8.
Solution:
Given:
Foci (± 3√5, 0) and the latus rectum is of length 8.
Here, the foci are on x-axis.
The equation of the hyperbola is of the form x2/a2 – y2/b2 = 1
Since the foci are (± 3√5, 0), so, c = ± 3√5
Length of latus rectum is 8
2b2/a = 8
2b2 = 8a
b2 = 8a/2
= 4a
It is known that a2 + b2 = c2
a2 + 4a = 45
a2 + 4a – 45 = 0
a2 + 9a – 5a – 45 = 0
(a + 9) (a -5) = 0
a = -9 or 5
Since a is non – negative, a = 5
So, b2 = 4a
= 4 × 5
= 20
∴ The equation of the hyperbola is x2/25 – y2/20 = 1
13. Foci (± 4, 0), the latus rectum is of length 12
Solution:
Given:
Foci (± 4, 0) and the latus rectum is of length 12
Here, the foci are on x-axis.
The equation of the hyperbola is of the form x2/a2 – y2/b2 = 1
Since the foci are (± 4, 0), so, c = 4
Length of latus rectum is 12
2b2/a = 12
2b2 = 12a
b2 = 12a/2
= 6a
It is known that a2 + b2 = c2
a2 + 6a = 16
a2 + 6a – 16 = 0
a2 + 8a – 2a – 16 = 0
(a + 8) (a – 2) = 0
a = -8 or 2
Since a is non – negative, a = 2
So, b2 = 6a
= 6 × 2
= 12
∴ The equation of the hyperbola is x2/4 – y2/12 = 1
14. Vertices (±7, 0), e = 4/3
Solution:
Given:
Vertices (±7, 0) and e = 4/3
Here, the vertices are on the x- axis
The equation of the hyperbola is of the form x2/a2 – y2/b2 = 1
Since the vertices are (± 7, 0), so, a = 7
It is given that e = 4/3
c/a = 4/3
3c = 4a
Substituting the value of a, we get
3c = 4(7)
c = 28/3
It is known that, a2 + b2 = c2
72 + b2 = (28/3)2
b2 = 784/9 – 49
= (784 – 441)/9
= 343/9
∴ The equation of the hyperbola is x2/49 – 9y2/343 = 1
15. Foci (0, ±√10), passing through (2, 3)
Solution:
Given:
Foci (0, ±√10) and passing through (2, 3)
Here, the foci are on y-axis.
The equation of the hyperbola is of the form y2/a2 – x2/b2 = 1
Since the foci are (±√10, 0), so, c = √10
It is known that a2 + b2 = c2
b2 = 10 – a2 ………….. (1)
It is given that the hyperbola passes through point (2, 3)
So, 9/a2 – 4/b2 = 1 … (2)
From equations (1) and (2), we get,
9/a2 – 4/(10-a2) = 1
9(10 – a2) – 4a2 = a2(10 –a2)
90 – 9a2 – 4a2 = 10a2 – a4
a4 – 23a2 + 90 = 0
a4 – 18a2 – 5a2 + 90 = 0
a2(a2 -18) -5(a2 -18) = 0
(a2 – 18) (a2 -5) = 0
a2 = 18 or 5
In hyperbola, c > a i.e., c2 > a2
So, a2 = 5
b2 = 10 – a2
= 10 – 5
= 5
∴ The equation of the hyperbola is y2/5 – x2/5 = 1
Miscellaneous EXERCISE PAGE NO: 264
1. If a parabolic reflector is 20 cm in diameter and 5 cm deep, find the focus.
Solution:
We know that the origin of the coordinate plane is taken at the vertex of the parabolic reflector, where the axis of the reflector is along the positive x – axis.
Diagrammatic representation is as follows:

We know that the equation of the parabola is of the form y2 = 4ax (as it is opening to the right)
Since the parabola passes through point A(10, 5),
y2 = 4ax
102 = 4a(5)
100 = 20a
a = 100/20
= 5
The focus of the parabola is (a, 0) = (5, 0), which is the mid-point of the diameter.
Hence, the focus of the reflector is at the mid-point of the diameter.
2. An arch is in the form of a parabola with its axis vertical. The arch is 10 m high and 5 m wide at the base. How wide is it 2 m from the vertex of the parabola?
Solution:
We know that the origin of the coordinate plane is taken at the vertex of the arch, where its vertical axis is along the positive y-axis.
Diagrammatic representation is as follows:

The equation of the parabola is of the form x2 = 4ay (as it is opening upwards).
It is given that at base arch is 10m high and 5m wide.
So, y = 10 and x = 5/2 from the above figure.
It is clear that the parabola passes through point (5/2, 10)
So, x2 = 4ay
(5/2)2 = 4a(10)
4a = 25/(4×10)
a = 5/32
we know the arch is in the form of a parabola whose equation is x2 = 5/8y
We need to find width, when height = 2m.
To find x, when y = 2.
When, y = 2,
x2 = 5/8 (2)
= 5/4
x = √(5/4)
= √5/2
AB = 2 × √5/2m
= √5m
= 2.23m (approx.)
Hence, when the arch is 2m from the vertex of the parabola, its width is approximately 2.23m.
3. The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100 m long is supported by vertical wires attached to the cable, the longest wire being 30 m and the shortest being 6 m.
Find the length of a supporting wire attached to the roadway 18 m from the middle.
Solution:
We know that the vertex is at the lowest point of the cable. The origin of the coordinate plane is taken as the vertex of the parabola, while its vertical axis is taken along the positive y –axis.
Diagrammatic representation is as follows:

Here, AB and OC are the longest and the shortest wires, respectively, attached to the cable.
DF is the supporting wire attached to the roadways, 18m from the middle.
So, AB = 30m, OC = 6m, and BC = 50m.
The equation of the parabola is of the from x2 = 4ay (as it is opening upwards).
The coordinates of point A are (50, 30 -6) = (50, 24)
Since A(50, 24) is a point on the parabola.
y2 = 4ax
(50)2 = 4a(24)
a = (50×50)/(4×24)
= 625/24
Equation of the parabola, x2 = 4ay = 4×(625/24)y or 6x2 = 625y
The x coordinate of point D is 18.
Hence, at x = 18,
6(18)2 = 625y
y = (6×18×18)/625
= 3.11(approx.)
Thus, DE = 3.11 m
DF = DE +EF = 3.11m +6m = 9.11m
Hence, the length of the supporting wire attached to the roadway 18m from the middle is approximately 9.11m.
4. An arch is in the form of a semi-ellipse. It is 8 m wide and 2 m high at the centre. Find the height of the arch at a point 1.5 m from one end.
Solution:
Since the height and width of the arc from the centre is 2m and 8m, respectively, it is clear that the length of the major axis is 8m, while the length of the semi-minor axis is 2m.
The origin of the coordinate plane is taken as the centre of the ellipse, while the major axis is taken along the x-axis.
Hence, Diagrammatic representation of semi-ellipse is as follows:

The equation of the semi-ellipse will be of the from x2/16 + y2/4 = 1, y ≥ 0 … (1
Let A be a point on the major axis such that AB = 1.5m.
Now draw AC ⊥ OB.
OA = (4 – 1.5)m = 2.5m
The x-coordinate of point C is 2.5
On substituting the value of x with 2.5 in equation (1), we get,
(2.5)2/16 + y2/4 = 1
6.25/16 + y2/4 = 1
y2 = 4 (1 – 6.25/16)
= 4 (9.75/16)
= 2.4375
y = 1.56 (approx.)
So, AC = 1.56m
Hence, the height of the arch at a point 1.5m from one end is approximately 1.56m.
5. A rod of length 12 cm moves with its ends always touching the coordinate axes. Determine the equation of the locus of a point P on the rod, which is 3 cm from the end in contact with the x-axis.
Solution:
Let AB be the rod making an angle Ɵ with OX and P(x,y) be the point on it such that
AP = 3cm.
Diagrammatic representation is as follows:
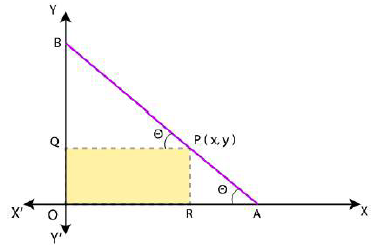
Then, PB = AB – AP = (12 – 3) cm = 9cm [AB = 12cm]
From P, draw PQ ⊥ OY and PR ⊥ OX.
In ΔPBQ, cos θ = PQ/PB = x/9
Sin θ = PR/PA = y/3
we know that, sin2 θ +cos2 θ = 1,
So,
(y/3)2 + (x/9)2 = 1 or
x2/81 + y2/9 = 1
Hence, the equation of the locus of point P on the rod is x2/81 + y2/9 = 1
6. Find the area of the triangle formed by the lines joining the vertex of the parabola x2 = 12y to the ends of its latus rectum.
Solution:
The given parabola is x2 = 12y.
On comparing this equation with x2 = 4ay, we get,
4a = 12
a = 12/4
= 3
The coordinates of foci are S(0,a) = S(0,3).
Now let AB be the latus rectum of the given parabola.
The given parabola can be roughly drawn as
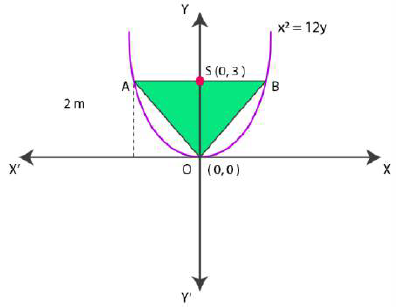
At y = 3, x2 = 12(3)
x2 = 36
x = ±6
So, the coordinates of A are (-6, 3), while the coordinates of B are (6, 3)
Then, the vertices of ΔOAB are O(0,0), A (-6,3) and B(6,3).
By using the formula,
Area of ΔOAB = ½ [0(3-3) + (-6)(3-0) + 6(0-3)] unit2
= ½ [(-6) (3) + 6 (-3)] unit2
= ½ [-18-18] unit2
= ½ [-36] unit2
= 18 unit2
∴ Area of ΔOAB is 18 unit2
7. A man running a racecourse notes that the sum of the distances from the two flag posts from him is always 10 m and the distance between the flag posts is 8 m.
Find the equation of the posts traced by the man.
Solution:
Let A and B be the positions of the two flag posts and P(x, y) be the position of the man.
So, PA + PB = 10.
We know that if a point moves in plane in such a way that the sum of its distance from two fixed point is constant, then the path is an ellipse, and this constant value is equal to the length of the major axis of the ellipse.
Then, the path described by the man is an ellipse where the length of the major axis is 10m, while points A and B are the foci.
Now let us take the origin of the coordinate plane as the centre of the ellipse, and taking the major axis along the x- axis,
The diagrammatic representation of the ellipse is as follows:
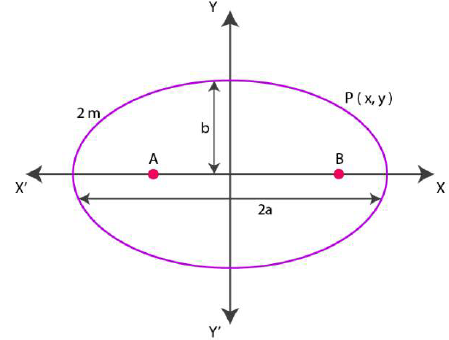
The equation of the ellipse is in the form of x2/a2 + y2/b2 = 1, where ‘a’ is the semi-major axis.
So, 2a = 10
a = 10/2
= 5
Distance between the foci, 2c = 8
c = 8/2
= 4
By using the relation, c = √(a2 – b2), we get,
4 = √(25 – b2)
16 = 25 – b2
b2 = 25 -1
= 9
b = 3
Hence, equation of the path traced by the man is x2/25 + y2/9 = 1
8. An equilateral triangle is inscribed in the parabola y2 = 4ax, where one vertex is at the vertex of the parabola. Find the length of the side of the triangle.
Solution:
Let us consider OAB be the equilateral triangle inscribed in parabola y2 = 4ax.
Let AB intersect the x-axis at point C.
Diagrammatic representation of the ellipse is as follows:

Now let OC = k
From the equation of the given parabola, we have,
So, y2 = 4ak
y = ±2√ak
The coordinates of points A and B are (k, 2√ak), and (k, -2√ak)
AB = CA + CB
= 2√ak + 2√ak
= 4√ak
Since, OAB is an equilateral triangle, OA2 = AB2.
Then,
k2 + (2√ak)2 = (4√ak)2
k2 + 4ak = 16ak
k2 = 12ak
k = 12a
Thus, AB = 4√ak = 4√(a×12a)
= 4√12a2
= 4√(4a×3a)
= 4(2)√3a
= 8√3a
Hence, the side of the equilateral triangle inscribed in parabola y2 = 4ax is 8√3a.
| Also Access |
| NCERT Exemplar for Class 11 Maths Chapter 11 |
| CBSE Notes for Class 11 Maths Chapter 11 |
NCERT Solutions for Class 11 Maths Chapter 11- Conic Sections
Chapter 11 Conic Sections of NCERT Solutions for Class 11 covers the topics listed below:
11.1 Introduction
11.2 Sections of a Cone
11.2.1 Circle, ellipse, parabola and hyperbola
11.2.2 Degenerated conic sections
11.3 Circle
11.4 Parabola
11.4.1 Standard equations of parabola
11.4.2 Latus rectum
11. 5 Ellipse
11.5.1 Relationship between semi-major axis, semi-minor axis and the distance of the focus from the centre of the ellipse
11.5.2 Special cases of an ellipse
11.5.3 Eccentricity
11.5.4 Standard equations of an ellipse
11.5.5 Latus rectum
11.6 Hyperbola
11.6.1 Eccentricity
11.6.2 Standard equation of Hyperbola
11.6.3 Latus rectum
Exercise 11.1 Solutions 15 Questions
Exercise 11.2 Solutions 12 Questions
Exercise 11.3 Solutions 20 Questions
Exercise 11.4 Solutions 15 Questions
Miscellaneous Exercise On Chapter 11 Solutions 8 Questions
NCERT Solutions for Class 11 Maths Chapter 11 – Conic Sections
The chapter Conic Sections belongs to the unit Coordinate Geometry, that adds up to 10 marks of the total 80 marks. The number of exercises is four and a miscellaneous exercise, adding to 5 exercises in total. Provided below are the concepts covered in this Chapter of NCERT Solutions for Class 11 Maths.
- A circle is the set of all points in a plane that are equidistant from a fixed point in the plane.
- The equation of a circle with centre (h, k) and the radius r is (x – h)2 + (y – k)2 = r2.
- A parabola is the set of all points in a plane that are equidistant from a fixed line and a fixed point in the plane.
- The equation of the parabola with focus at (a, 0) a > 0 and directrix x = – a is y2 = 4ax.
- Latus rectum of a parabola is a line segment perpendicular to the axis of the parabola, through the focus and whose endpoints lie on the parabola.
- Length of the latus rectum of the parabola y2 = 4ax is 4a.
- An ellipse is the set of all points in a plane, the sum of whose distances from two fixed points in the plane is constant.
- The equation of an ellipse with foci on the x-axis.
- Latus rectum of an ellipse is a line segment perpendicular to the major axis through any of the foci and whose endpoints lie on the ellipse.
- Length of the latus rectum of the ellipse.
- The eccentricity of an ellipse is the ratio between the distances from the centre of the ellipse to one of the foci and to one of the vertices of the ellipse.
- A hyperbola is the set of all points in a plane, the difference of whose distances from two fixed points in the plane is constant.
- The equation of a hyperbola with foci on the x-axis.
- Latus rectum of a hyperbola is a line segment perpendicular to the transverse axis through any of the foci and whose endpoints lie on the hyperbola.
- Length of the latus rectum of the hyperbola.
- The eccentricity of a hyperbola is the ratio of the distances from the centre of the hyperbola to one of the foci and to one of the vertices of the hyperbola.
Studying the Conic Sections of Class 11 enables the students to get a strong knowledge of the concepts of Sections of a cone: circles, ellipse, parabola, hyperbola, a point, a straight line and a pair of intersecting lines as a degenerate case of a conic section. The students would also be able to understand the standard equations and simple properties of parabola, ellipse, hyperbola and circle.
Disclaimer –
Dropped Topics – 11.5.2 Special Cases of an Ellipse




















































Comments