RD Sharma Solutions for Class 8 Maths Chapter 20 Mensuration - I (Area of a Trapezium and a Polygon) Exercise 20.1

In Exercise 20.1 of Chapter 20, we shall discuss the basic application of formulae based on squares, rectangles, triangles, parallelograms, rhombuses, etc. Solutions given here are prepared by the subject experts, keeping in mind the latest CBSE syllabus, to help students score well in the final exam. To grasp the concepts better, students can refer to RD Sharma Class 8 Solutions and download the PDF from the links provided below. Students are advised to practise on a regular basis to enhance their confidence level.

RD Sharma Solutions for Class 8 Maths Exercise 20.1 Chapter 20 Mensuration – I (Area of a Trapezium and a Polygon)

Download PDF

carouselExampleControls111

Previous



Next

Access answers to RD Sharma Maths Solutions for Class 8 Exercise 20.1 Chapter 20 Mensuration – I (Area of a Trapezium and a Polygon)

1. A flooring tile has the shape of a parallelogram whose base is 24 cm, and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m²?

Solution:

Given that,

Base of parallelogram = 24cm

Height of parallelogram = 10cm

Area of floor = 1080m²

We know that,

Area of parallelogram = Base × Height

Area of 1 tile = 24 × 10 = 240cm²

We know that, 1m = 100cm

So for 1080m² = 1080 × 100 × 100 cm²

To calculate the Number of tiles required = Area of floor/Area of 1 tile

i.e., Number of tiles required = (1080 × 100 × 100) / (24 × 10) = 45000

∴ Number of tiles required = 45000

2. A plot is in the form of a rectangle ABCD having semi-circle on BC, as shown in Fig. 20.23. If AB = 60 m and BC = 28 m, Find the area of the plot.

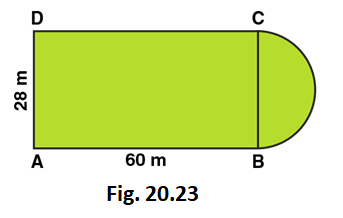
Solution:

Area of the plot = Area of the rectangle + Area of semi-circle

Radius of semi-circle = BC/2 = 28/2 = 14m

Area of the Rectangular plot = Length × Breadth = 60 × 28 = 1680 m²

Area of the Semi-circular portion = πr²/2

= 1/2 × 22/7 × 14 × 14

= 308 m²

∴ The total area of the plot = 1680 + 308 = 1988 m²

3. A playground has the shape of a rectangle, with two semi-circles on its smaller sides as diameters, added to its outside. If the sides of the rectangle are 36 m and 24.5 m, find the area of the playground. (Take π= 22/7.)

Solution:

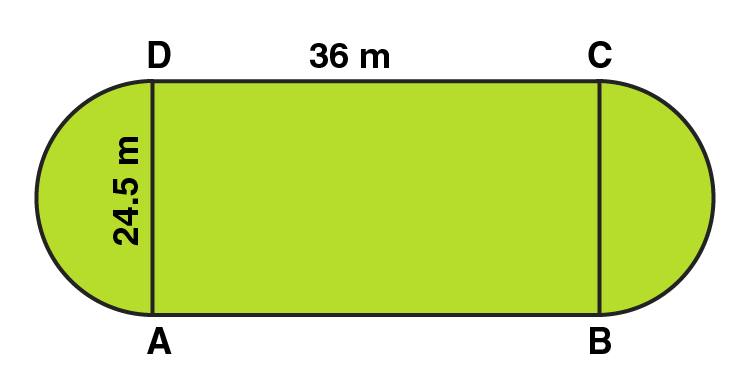
Area of the plot = Area of the Rectangle + 2 × area of one semi-circle

Radius of semi-circle = BC/2 = 24.5/2 = 12.25m

Area of the Rectangular plot = Length × Breadth = 36 × 24.5 = 882 m²

Area of the Semi-circular portions = 2 × πr²/2

= 2 × 1/2 × 22/7 × 12.25 × 12.25 = 471.625 m²

Area of the plot = 882 + 471.625 = 1353.625 m²

4. A rectangular piece is 20 m long and 15 m wide. From its four corners, quadrants of radii 3.5 m have been cut. Find the area of the remaining part.

Solution:

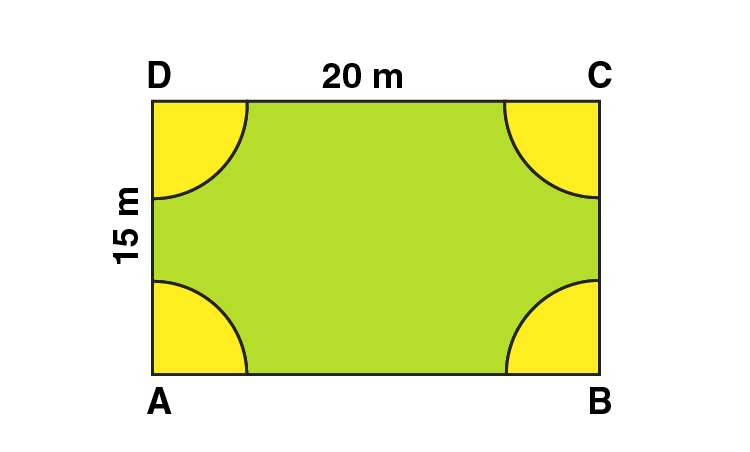
Area of the plot = Area of the rectangle – 4 × area of one quadrant

Radius of semi-circle = 3.5 m

Area of four quadrants = area of one circle

Area of the plot = Length × Breadth – πr²

Area of the plot = 20 × 15 – (22/7 × 3.5 × 3.5)

Area of the plot = 300 – 38.5 = 261.5 m²

5. The inside perimeter of a running track (shown in Fig. 20.24) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If track is everywhere 14 m wide, find the area of the track. Also, find the length of the outer running track.

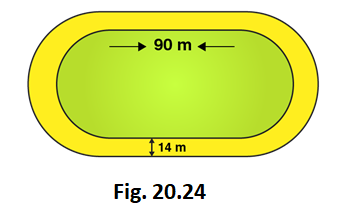
Solution:

Perimeter of the inner track = 2 × Length of rectangle + perimeter of two semi-circular ends

Perimeter of the inner track = Length + Length + 2πr

400 = 90 + 90 + (2 × 22/7 × r)

(2 × 22/7 × r) = 400 – 180

(2 × 22/7 × r) = 220

44r = 220 × 7

44r = 1540

r = 1540/44 = 35

r = 35m

So, the radius of inner circle = 35 m

Now, let’s calculate the radius of outer track

Radius of outer track = Radius of inner track + width of the track

Radius of outer track = 35 + 14 = 49m

Length of outer track = 2× Length of rectangle + perimeter of two outer semi-circular ends

Length of outer track = 2× 90 + 2πr

Length of outer track = 2× 90 + (2 × 22/7 × 49)

Length of outer track = 180 + 308 = 488

So, Length of outer track = 488m

Area of inner track = Area of inner rectangle + Area of two inner semi-circles

Area of inner track = Length × Breadth + πr²

Area of inner track = 90 × 70 + (22/7 × 35 × 35)

Area of inner track = 6300 + 3850

So, Area of inner track = 10150 m²

Area of outer track = Area of outer rectangle + Area of two outer semi-circles

Breadth of outer track = 35 + 35 +14 + 14 = 98 m

Area of outer track = length× breadth + πr²

Area of outer track = 90 × 98 + (22/7 × 49 × 49)

Area of outer track = 8820 + 7546

So, Area of outer track = 16366 m²

Now, let’s calculate area of path

Area of path = Area of outer track – Area of inner track

Area of path = 16366 – 10150 = 6216

So, Area of path = 6216 m²

6. Find the area of Fig. 20.25, in square cm, correct to one place of decimal. (Take π =22/7)

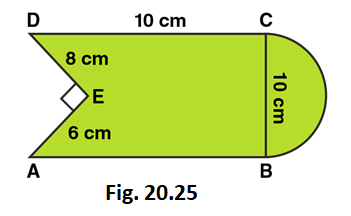
Solution:

Area of the Figure = Area of square + Area of semi-circle – Area of right angled triangle

Area of the Figure = side × side + πr²/2 – (1/2 × base × height)

Area of the Figure = 10 × 10 + (1/2 × 22/7 × 5 × 5) – (1/2 × 8 × 6)

Area of the Figure = 100 + 39.28 – 24

Area of the Figure = 115.3

So, Area of the Figure = 115.3 cm²

7. The diameter of a wheel of a bus is 90 cm which makes 315 revolutions per minute. Determine its speed in kilometres per hour. (Take π=22/7)

Solution:

Given that, Diameter of a wheel = 90 cm

We know that, Perimeter of wheel = πd

Perimeter of wheel = 22/7 × 90 = 282.857

So, Perimeter of a wheel = 282.857 cm

Distance covered in 315 revolutions = 282.857× 315 = 89099.955 cm

One km = 100000 cm

Therefore, Distance covered = 89099.955/100000 = 0.89 km

Speed in km per hour = 0.89 × 60 = 53.4 km per hour

8. The area of a rhombus is 240 cm² and one of the diagonal is 16 cm. Find another diagonal.

Solution:

Area of rhombus = 1/2 × d₁ × d₂

240 = 1/2 × 16 × d₂

240 = 8 × d₂

d₂ = 240/8 = 30

So, the other diagonal is 30 cm

9. The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.

Solution:

Area of rhombus = 1/2 × d₁ × d₂

Area of rhombus = 1/2 × 7.5 × 12

Area of rhombus = 6 × 7.5 = 45

So, Area of rhombus = 45 cm²

10. The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.

Solution:

Area of quadrilateral = 1/2 × d₁ × (p₁ + p₂)

Area of quadrilateral = 1/2 × 24 × (8 + 13)

Area of quadrilateral = 12 × 21 = 252

So, Area of quadrilateral is 252 cm²

11. Find the area of a rhombus whose side is 6 cm and whose altitude is 4 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.

Solution:

Given that,

Side of rhombus = 6 cm

Altitude of rhombus = 4 cm

Since rhombus is a parallelogram, therefore area of parallelogram = base × altitude

i.e., Area of parallelogram = 6 × 4 = 24 cm²

Area of parallelogram = Area of rhombus

Area of rhombus = 1/2 × d₁ × d₂

24 = 1/2 × 8 × d₂

24 = 4 × d₂

d₂ = 24/4 = 6

So, length of other diagonal of rhombus is 6 cm

12. The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per m² is Rs. 4.

Solution:

We know that,

Area of rhombus = 1/2 × d₁ × d₂

Area of rhombus = 1/2 × 45 × 30

Area of rhombus = 1350/2 = 675

So, Area of rhombus = 675 cm²

∴ Area of one tile = 675 cm²

Now, Area of 3000 tiles = 675× 3000 = 2025000 cm²

Area of tiles in m² = 2025000/10000 = 202.5 m²

Total cost for polishing the floor = 202.5× 4 = Rs 810

13. A rectangular grassy plot is 112 m long and 78 m broad. It has gravel path 2.5 m wide all around it on the side. Find the area of the path and the cost of constructing it at Rs. 4.50 per square metre.

Solution:

We know that,

Outer area of rectangle = length × breadth

Outer area of rectangle = 112 × 78 = 8736 m²

Width of path = 2.5 m

Length of inner rectangle = 112 – (2.5 + 2.5) = 107 m

Breadth of inner rectangle = 78 – (2.5 + 2.5) = 73 m

And,

Inner area of rectangle = length × breadth

Inner area of rectangle = 107 × 73 = 7811 m²

Now let’s calculate Area of path,

Area of path = Outer area of rectangle – Inner area of rectangle

Area of path = 8736 – 7811 = 925 m²

Also given that,

Cost of construction for 1 m² = Rs 4.50

∴ Cost of construction for 925 m² = 925 × 4.50 = Rs 4162.5

14. Find the area of a rhombus, each side of which measures 20 cm and one of whose diagonals is 24 cm.

Solution:

Given that,

Length of side of rhombus = 20 cm

Length of one diagonal = 24 cm

In ΔAOB,

Using Pythagoras theorem:

AB² = OA² + OB²

20² = 12² + OB²

OB² = 20² – 12²

OB² = 400 – 144

OB² = 256

OB = 16

So, length of the other diameter = 16 × 2 = 32 cm

Area of rhombus = 1/2 × d₁ × d₂

Area of rhombus = 1/2 × 24 × 32

Area of rhombus = 384 cm²

15. The length of a side of a square field is 4 m. What will be the altitude of the rhombus, if the area of the rhombus is equal to the square field and one of its diagonal is 2 m?

Solution:

Given that,

Length of a side of a square = 4 m

Area of square = side²

Area of square = 4 × 4 = 16 m²

We know that,

Area of square = Area of rhombus

So, Area of rhombus = 16 m²

Area of rhombus = 1/2 × d₁ × d₂

16 = 1/2 × 2 × d₂

16 = d₂

∴ the diagonal of rhombus = 16 m

In ΔAOB,

Using Pythagoras theorem:

AB² = OA² + OB²

AB² = 8² + 1²

AB² = 65

AB = √65

Since rhombus is a parallelogram, therefore area of parallelogram = base × altitude

Area of parallelogram = AB × DE

16 = √65 × DE

DE = 16/√65

i.e., Altitude of Rhombus = 16/√65 cm

16. Find the area of the field in the form of a rhombus, if the length of each side be 14 cm and the altitude be 16 cm.

Solution:

Given that,

Side of rhombus = 14 cm

Altitude of rhombus = 16 cm

Since rhombus is a parallelogram, therefore

Area of parallelogram = base × altitude

Area of parallelogram = 14 × 16 = 224 cm²

17. The cost of fencing a square field at 60 paise per metre is Rs. 1200. Find the cost of reaping the field at the rate of 50 paise per 100 sq. metres.

Solution:

Perimeter of square field = Cost of fencing / rate of fencing

Perimeter of square field = 1200/0.6 = 2000

So, Perimeter of square field = 2000 m

Perimeter of square = 4 × side

Side of square = Perimeter / 4 = 2000/4 = 500

So, Side of square = 500 m

We know that, Area of square = side²

Area of square = 500 × 500 = 250000 m²

Cost of reaping = (250000 × 0.5) / 100 = 1250

∴ Cost of reaping the field is Rs 1250

18. In exchange of a square plot one of whose sides is 84 m, a man wants to buy a rectangular plot 144 m long and of the same area as of the square plot. Find the width of the rectangular plot.

Solution:

Area of square = side²

Area of square = 84 × 84 = 7056

Since, Area of square = Area of rectangle

7056 = 144 × width

Width = 7056/144 = 49

∴ Width of rectangle = 49 m

19. The area of a rhombus is 84 m². If its perimeter is 40 m, then find its altitude.

Solution:

Given that,

Area of rhombus = 84 m²

Perimeter = 40 m

We know that,

Perimeter of rhombus = 4 × side

∴ Side of rhombus = Perimeter / 4 = 40/4 = 10

So, Side of rhombus = 10 m

Since rhombus is a parallelogram, therefore Area of parallelogram = base × altitude

84 = 10 × altitude

Altitude = 84/10 = 8.4

So, Altitude of rhombus = 8.4 m

20. A garden is in the form of a rhombus whose side is 30 metres and the corresponding altitude is 16 m. Find the cost of levelling the garden at the rate of Rs. 2 per m².

Solution:

Given that,

Side of rhombus = 30 m

Altitude of rhombus = 16 m

Since rhombus is a parallelogram, therefore Area of parallelogram = base × altitude

Area of parallelogram = 30 × 16 = 480 m²

Cost of levelling the garden = area × rate

Cost of levelling the garden = 480 × 2 = 960

So, Cost of levelling the garden is Rs 960

21. A field in the form of a rhombus has each side of length 64 m and altitude 16 m. What is the side of a square field which has the same area as that of a rhombus?

Solution:

Given that,

Side of rhombus = 64 m

Altitude of rhombus = 16 m

Since rhombus is a parallelogram, therefore Area of parallelogram = base × altitude

Area of parallelogram = 64 × 16 = 1024 m²

Since Area of rhombus = Area of square

Therefore, Area of square = side²

Or side² = Area of square

Side of a square = √square

Side of square = √1024 = 32

∴ Side of square = 32 m

22. The area of a rhombus is equal to the area of a triangle whose base and the corresponding altitude are 24.8 cm and 16.5 cm, respectively. If one of the diagonals of the rhombus is 22 cm, find the length of the other diagonal.

Solution:

Given that,

Length of base of triangle = 24.8 cm

Length of altitude of triangle= 16.5 cm

∴ Area of triangle = 1/2 × base × altitude

Area of triangle = 1/2 × 24.8 × 16.5 = 204.6

So, Area of triangle = 204.6 cm

Since, Area of triangle = Area of rhombus

∴ Area of rhombus = 1/2 × d₁ × d₂

204.6 = 1/2 × 22 × d₂

204.6 = 11 × d₂

d₂ = 204.6/11 = 18.6

∴ The length of other diagonal is 18.6 cm.