In Exercise 20.2 of Chapter 20, students shall learn the area of a trapezium. Students who find it difficult to solve problems can refer to RD Sharma Class 8 Solutions, crafted by our subject experts. Solutions given here are prepared in simple and understandable language to help students score well in the final exam. Students can easily download the PDF from the links provided below and start practising offline.
RD Sharma Solutions for Class 8 Maths Exercise 20.2 Chapter 20 Mensuration – I (Area of a Trapezium and a Polygon)
Access answers to RD Sharma Maths Solutions for Class 8 Exercise 20.2 Chapter 20 Mensuration – I (Area of a Trapezium and a Polygon)
1. Find the area, in square metres, of the trapezium whose bases and altitudes are as under:
(i) bases = 12 dm and 20 dm, altitude = 10 dm
(ii) bases = 28 cm and 3 dm, altitude = 25 cm
(iii) bases = 8 m and 60 dm, altitude = 40 dm
(iv) bases = 150 cm and 30 dm, altitude = 9 dm
Solution:
(i) Given that,
Length of bases of trapezium = 12 dm and 20 dm
Length of altitude = 10 dm
We know that, 10 dm = 1 m
∴ Length of bases in m = 1.2 m and 2 m
Similarly, length of altitude in m = 1 m
Area of trapezium = 1/2 (Sum of lengths of parallel sides) × altitude
Area of trapezium = 1/2 (1.2 + 2.0) × 1
Area of trapezium = 1/2 × 3.2 = 1.6
So, Area of trapezium = 1.6m2
(ii) Given that,
Length of bases of trapezium = 28 cm and 3 dm
Length of altitude = 25 cm
We know that, 10 dm = 1 m
∴ Length of bases in m = 0.28 m and 0.3 m
Similarly, length of altitude in m = 0.25 m
Area of trapezium = 1/2 (Sum of lengths of parallel sides) × altitude
Area of trapezium = 1/2 (0.28 + 0.3) × 0.25
Area of trapezium = 1/2 × 0.58× 0.25 = 0.0725
So, Area of trapezium = 0.0725m2
(iii) Given that,
Length of bases of trapezium = 8 m and 60 dm
Length of altitude = 40 dm
We know that, 10 dm = 1 m
∴ Length of bases in m = 8 m and 6 m
Similarly, length of altitude in m = 4 m
Area of trapezium = 1/2 (Sum of lengths of parallel sides) × altitude
Area of trapezium = 1/2 (8 + 6) × 4
Area of trapezium = 1/2 × 56 = 28
So, Area of trapezium = 28m2
(iv) Given that,
Length of bases of trapezium = 150 cm and 30 dm
Length of altitude = 9 dm
We know that, 10 dm = 1 m
∴ Length of bases in m = 1.5 m and 3 m
Similarly, length of altitude in m = 0.9 m
Area of trapezium = 1/2 (Sum of lengths of parallel sides) × altitude
Area of trapezium = 1/2 (1.5 + 3) × 0.9
Area of trapezium = 1/2 × 4.5 × 0.9 = 2.025
So, Area of trapezium = 2.025m2
2. Find the area of trapezium with base 15 cm and height 8 cm, if the side parallel to the given base is 9 cm long.
Solution:
Given that,
Length of bases of trapezium = 15 cm and 9 cm
Length of altitude = 8 cm
We know that,
Area of trapezium = 1/2 (Sum of lengths of parallel sides) × altitude
Area of trapezium = 1/2 (15 + 9) × 8
Area of trapezium = 1/2 × 192 = 96
So, Area of trapezium = 96m2
3. Find the area of a trapezium whose parallel sides are of length 16 dm and 22 dm and whose height is 12 dm.
Solution:
Given that,
Length of bases of trapezium = 16 dm and 22 dm
Length of altitude = 12 dm
We know that, 10 dm = 1 m
∴ Length of bases in m = 1.6 m and 2.2 m
Similarly, length of altitude in m = 1.2 m
Area of trapezium = 1/2 (Sum of lengths of parallel sides) × altitude
Area of trapezium = 1/2 (1.6 + 2.2) × 1.2
Area of trapezium = 1/2 × 3.8 × 1.2 = 2.28
So, Area of trapezium = 2.28m2
4. Find the height of a trapezium, the sum of the lengths of whose bases (parallel sides) is 60 cm and whose area is 600 cm2.
Solution:
Given that,
Length of bases of trapezium = 60 cm
Area = 600 cm2
We know that,
Area of trapezium = 1/2 (Sum of lengths of parallel sides) × altitude
600 = 1/2 (60) × altitude
600 = 30 × altitude
Which implies, altitude = 600/30 = 20
∴ Length of altitude is 20 cm
5. Find the altitude of a trapezium whose area is 65 cm2 and whose base are 13 cm and 26 cm.
Solution:
Given that,
Length of bases of trapezium = 13 cm and 26 cm
Area = 65 cm2
We know that,
Area of trapezium = 1/2 (Sum of lengths of parallel sides) × altitude
65 = 1/2 (13 + 26) × altitude
65 = 39/2 × altitude
Which implies, altitude = (65×2) /39 = 130/39 = 10/3
∴ Length of altitude = 10/3 cm
6. Find the sum of the lengths of the bases of a trapezium whose area is 4.2 m2 and whose height is 280 cm.
Solution:
Given that,
Height of trapezium = 280 cm = 2.8m
Area = 4.2 m2
We know that,
Area of trapezium = 1/2 (Sum of lengths of parallel sides) × altitude To calculate the length of parallel sides we can rewrite the above equation as,
Sum of lengths of parallel sides = (2 × Area) / altitude
Sum of lengths of parallel sides = (2 × 4.2) / 2.8 = 8.4/2.8 = 3
∴ Sum of lengths of parallel sides = 3 m
7. Find the area of a trapezium whose parallel sides of lengths 10 cm and 15 cm are at a distance of 6 cm from each other. Calculate this area as,
(i) the sum of the areas of two triangles and one rectangle.
(ii) the difference of the area of a rectangle and the sum of the areas of two triangles.
Solution:
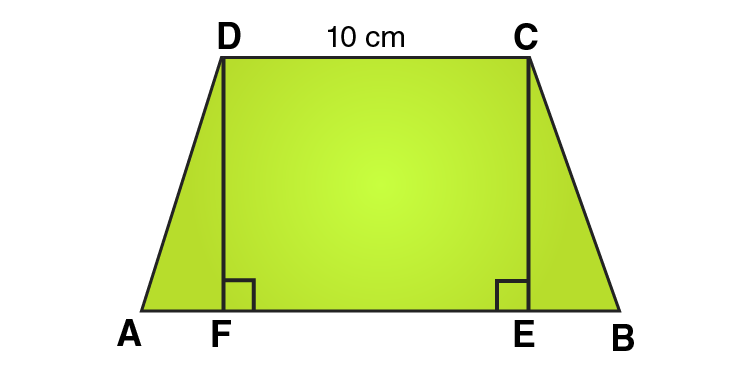
We know that, Area of a trapezium ABCD
= area (∆DFA) + area (rectangle DFEC) + area (∆CEB)
= (1/2 × AF × DF) + (FE × DF) + (1/2 × EB × CE)
= (1/2 × AF × h) + (FE × h) + (1/2 × EB × h)
= 1/2 × h × (AF + 2FE + EB)
= 1/2 × h × (AF + FE + EB + FE)
= 1/2 × h × (AB + FE)
= 1/2 × h × (AB + CD) [Opposite sides of rectangle are equal]
= 1/2 × 6 × (15 + 10)
= 1/2 × 6 × 25 = 75
∴ Area of trapezium = 75 cm2
8. The area of a trapezium is 960 cm2. If the parallel sides are 34 cm and 46 cm, find the distance between them.
Solution:
We know that,
Area of trapezium = 1/2 (Sum of lengths of parallel sides) × distance between parallel sides
i.e., Area of trapezium = 1/2 (Sum of sides) × distance between parallel sides
To calculate the distance between parallel sides we can rewrite the above equation as,
Distance between parallel sides = (2 × Area) / Sum of sides
= (2 × 960) / (34 + 46)
= (2 × 960) / 80 = 1920/80 = 24
∴ Distance between parallel sides = 24 cm
9. Find the area of Fig. 20.35 as the sum of the areas of two trapezium and a rectangle.
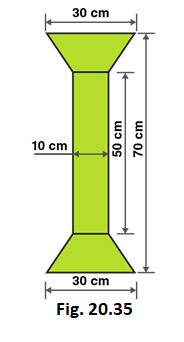
Solution:
From the figure we can write,
Area of figure = Area of two trapeziums + Area of rectangle
Given that,
Length of rectangle = 50 cm
Breadth of rectangle = 10 cm
Length of parallel sides of trapezium = 30 cm and 10 cm
Distance between parallel sides of trapezium = (70–50)/2 = 20/2 = 10
So, Distance between parallel sides of trapezium = 10 cm
Area of figure = 2 × 1/2 (Sum of lengths of parallel sides) × altitude + Length × Breadth
Area of figure = 2 × 1/2 (30+10) × 10 + 50 × 10
Area of figure = 40 × 10 + 50 × 10
Area of figure = 400 + 500 = 900
∴ Area of figure = 900 cm2
10. Top surface of a table is trapezium in shape. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.
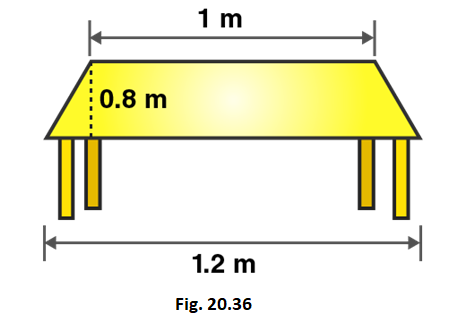
Solution:
Given that,
Length of parallel sides of trapezium = 1.2m and 1m
Distance between parallel sides of trapezium = 0.8m
We know that,
Area of trapezium = 1/2 (Sum of lengths of parallel sides) × distance between parallel sides
i.e., Area of trapezium = 1/2 (Sum of sides) × distance between parallel sides
Area of trapezium = 1/2 (1.2 + 1) × 0.8
Area of trapezium = 1/2 × 2.2 × 0.8 = 0.88
So, Area of trapezium = 0.88m2
11. The cross-section of a canal is a trapezium in shape. If the canal is 10 m wide at the top 6 m wide at the bottom and the area of cross-section is 72 m2 determine its depth.
Solution:
Given that,
Length of parallel sides of trapezium = 10m and 6m
Area = 72 m2
Let the distance between parallel sides of trapezium = x meter
We know that,
Area of trapezium = 1/2 (Sum of lengths of parallel sides) × distance between parallel sides
i.e., Area of trapezium = 1/2 (Sum of sides) × distance between parallel sides
72 = 1/2 (10 + 6) × x
72 = 8 × x
x = 72/8 = 9
∴ The depth is 9m.
12. The area of a trapezium is 91 cm2 and its height is 7 cm. If one of the parallel sides is longer than the other by 8 cm, find the two parallel sides.
Solution:
Given that,
Let the length of one parallel side of trapezium = x meter
Length of other parallel side of trapezium = (x+8) meter
Area of trapezium = 91 cm2
Height = 7 cm
We know that,
Area of trapezium = 1/2 (Sum of lengths of parallel sides) × altitude
91 = 1/2 (x+x+8) × 7
91 = 1/2(2x+8) × 7
91 = (x+4) × 7
(x+4) = 91/7
x+4 = 13
x = 13 – 4
x = 9
∴ Length of one parallel side of trapezium = 9 cm
And, Length of other parallel side of trapezium = x+8 = 9+8 = 17 cm
13. The area of a trapezium is 384 cm2. Its parallel sides are in the ratio 3:5 and the perpendicular distance between them is 12 cm. Find the length of each one of the parallel sides.
Solution:
Given that,
Let the length of one parallel side of trapezium = 3x meter
Length of other parallel side of trapezium = 5x meter
Area of trapezium = 384 cm2
Distance between parallel sides = 12 cm
We know that,
Area of trapezium = 1/2 (Sum of lengths of parallel sides) × distance between parallel sides
i.e., Area of trapezium = 1/2 (Sum of sides) × distance between parallel sides
384 = 1/2 (3x + 5x) × 12
384 = 1/2 (8x) × 12
4x = 384/12
4x = 32
x = 8
∴ Length of one parallel side of trapezium = 3x = 3× 8 = 24 cm
And, Length of other parallel side of trapezium = 5x = 5× 8 = 40 cm
14. Mohan wants to buy a trapezium shaped field. Its side along the river is parallel and twice the side along the road. If the area of this field is 10500 m2 and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.
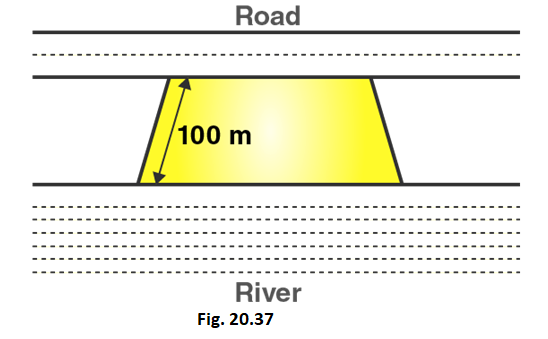
Solution:
Given that,
Let the length of side of trapezium shaped field along road = x meter
Length of other side of trapezium shaped field along road = 2x meter
Area of trapezium = 10500 cm2
Distance between parallel sides = 100 m
We know that,
Area of trapezium = 1/2 (Sum of lengths of parallel sides) × distance between parallel sides
i.e., Area of trapezium = 1/2 (Sum of sides) × distance between parallel sides
10500 = 1/2 (x + 2x) × 100
10500 = 1/2 (3x) × 100
3x = 10500/50
3x = 210
x = 210/3 = 70
x = 70
∴ Length of side of trapezium shaped field along road = 70 m
And, Length of other side of trapezium shaped field along road = 2x = 70× 2 = 140 m
15. The area of a trapezium is 1586 cm2 and the distance between the parallel sides is 26 cm. If one of the parallel sides is 38 cm, find the other.
Solution:
Given that,
Let the length of other parallel side of trapezium = x cm
Length of one parallel side of trapezium = 38 cm
Area of trapezium = 1586 cm2
Distance between parallel sides = 26 cm
We know that,
Area of trapezium = 1/2 (Sum of lengths of parallel sides) × distance between parallel sides
i.e., Area of trapezium = 1/2 (Sum of sides) × distance between parallel sides
1586 = 1/2 (x + 38) × 26
1586 = (x + 38) × 13
(x + 38) = 1586/13
x = 122 – 38
x =84
∴ Length of the other parallel side of trapezium = 84 cm
16. The parallel sides of a trapezium are 25 cm and 13 cm; its nonparallel sides are equal, each being 10 cm, find the area of the trapezium.
Solution:
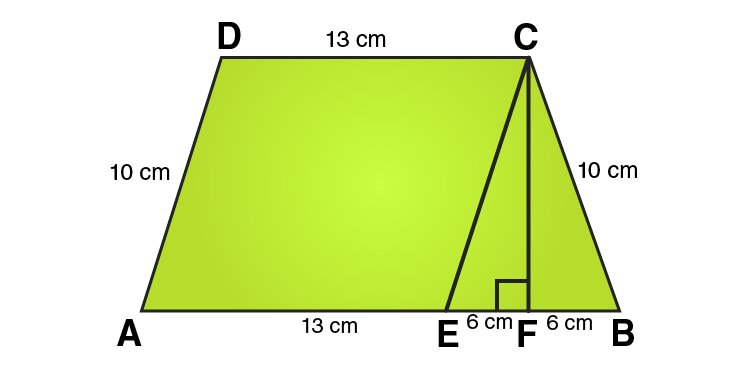
In ΔCEF,
CE = 10 cm and EF = 6cm
Using Pythagoras theorem:
CE2 = CF2 + EF2
CF2 = CE2 – EF2
CF2 = 102 – 62
CF2 = 100-36
CF2 = 64
CF = 8 cm
From the figure we can write,
Area of trapezium = Area of parallelogram AECD + Area of area of triangle CEF
Area of trapezium = base × height + 1/2 (base × height)
Area of trapezium = 13 × 8 + 1/2 (12 × 8)
Area of trapezium = 104 + 48 = 152
∴ Area of trapezium = 152 cm2
17. Find the area of a trapezium whose parallel sides are 25 cm, 13 cm and the other sides are 15 cm each.
Solution:
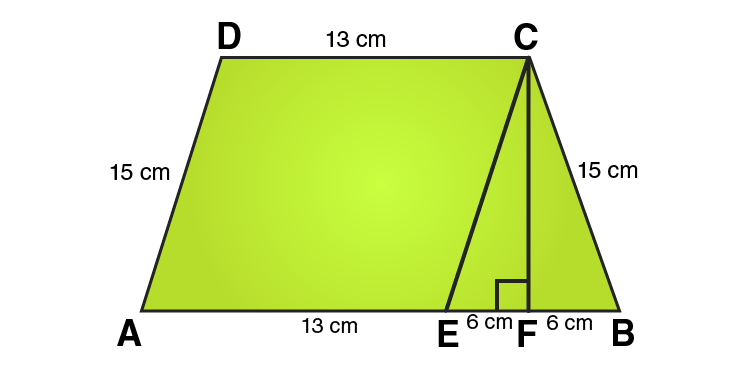
In ΔCEF,
CE = 10 cm and EF = 6cm
Using Pythagoras theorem:
CE2 = CF2 + EF2
CF2 = CE2 – EF2
CF2 = 152 – 62
CF2 = 225-36
CF2 = 189
CF = √189
= √ (9×21)
= 3√21 cm
From the figure we can write,
Area of trapezium = Area of parallelogram AECD + Area of area of triangle CEF
Area of trapezium = height + 1/2 (sum of parallel sides)
Area of trapezium = 3√21 × 1/2 (25 + 13)
Area of trapezium = 3√21 × 19 = 57√21
∴ Area of trapezium = 57√21 cm2
18. If the area of a trapezium is 28 cm2 and one of its parallel sides is 6 cm, find the other parallel side if its altitude is 4 cm.
Solution:
Given that,
Let the length of other parallel side of trapezium = x cm
Length of one parallel side of trapezium = 6 cm
Area of trapezium = 28 cm2
Length of altitude of trapezium = 4 cm
We know that,
Area of trapezium = 1/2 (Sum of lengths of parallel sides) × distance between parallel sides
i.e., Area of trapezium = 1/2 (Sum of sides) × distance between parallel sides
28 = 1/2 (6 + x) × 4
28 = (6 + x) × 2
(6 + x) = 28/2
(6 + x) = 14
x = 14 – 6
x = 8
∴ Length of the other parallel side of trapezium = 8 cm
19. In Fig. 20.38, a parallelogram is drawn in a trapezium, the area of the parallelogram is 80 cm2, find the area of the trapezium.
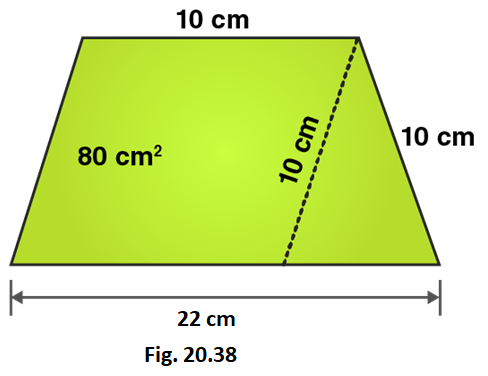
Solution:
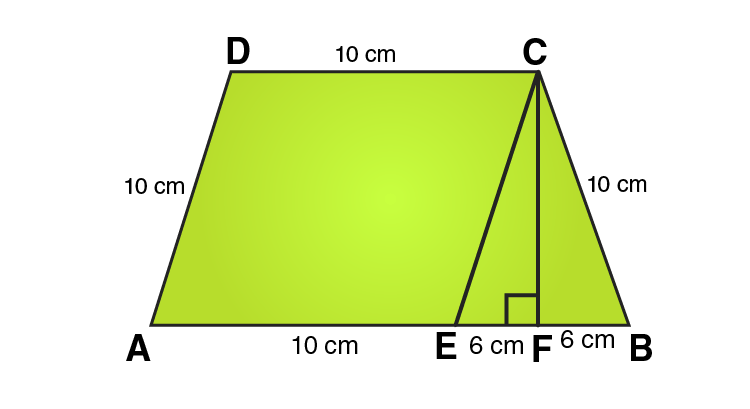
In ΔCEF,
CE = 10 cm and EF = 6cm
Using Pythagoras theorem:
CE2 = CF2 + EF2
CF2 = CE2 – EF2
CF2 = 102 – 62
CF2 = 100-36
CF2 = 64
CF = 8 cm
Area of parallelogram = 80 cm2
From the figure we can write,
Area of trapezium = Area of parallelogram AECD + Area of area of triangle CEF
Area of trapezium = base × height + 1/2 (base × height)
Area of trapezium = 10 × 8 + 1/2 (12 × 8)
Area of trapezium = 80 + 48 = 128
∴ Area of trapezium = 128 cm2
20. Find the area of the field shown in Fig. 20.39 by dividing it into a square, a rectangle and a trapezium.
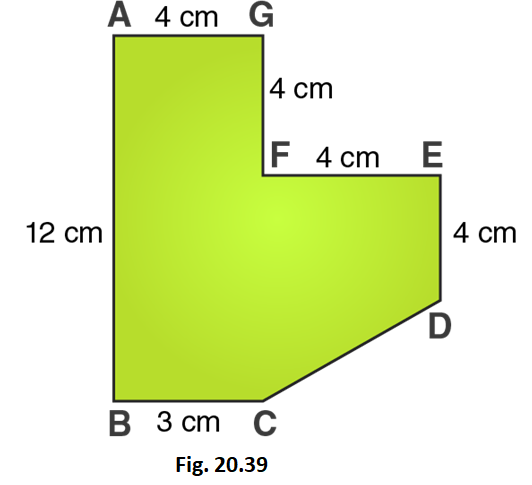
Solution:
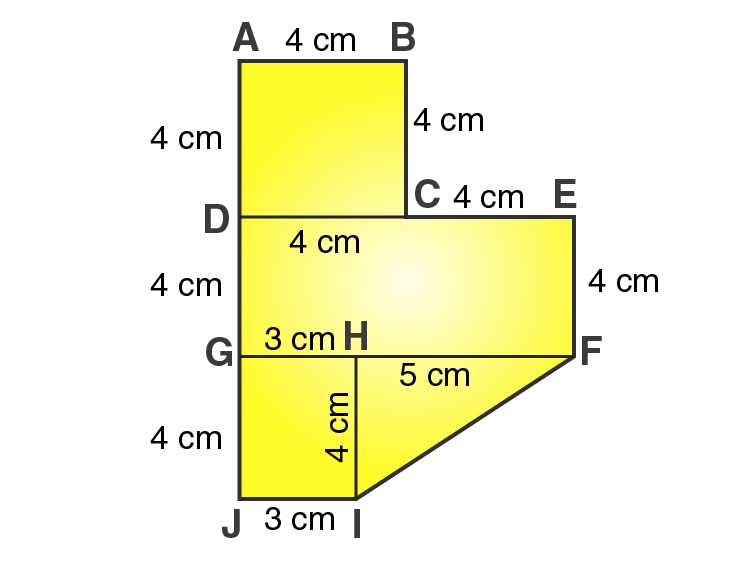
From the figure, we can write,
Area of given figure = Area of square ABCD + Area of rectangle DEFG + Area of rectangle GHIJ + Area of triangle FHI
i.e., Area of given figure = side × side + length × breadth + length × breadth + 1/2 × base × altitude
Area of given figure = 4×4 + 8×4 + 3×4 + 1/2×5×5
Area of given figure = 16 + 32 + 12 + 10 = 70
∴ Area of given figure = 70 cm2














Comments