RD Sharma Solutions for Class 12 Maths Exercise 11.1 Chapter 11 Differentiation is provided here. RD Sharma Solutions are one of the best resource materials currently available for students who aspire to score well in Maths. The quality of these study materials makes them an excellent guide for the students to succeed in the examination.
BYJU’S brings you the RD Sharma Solutions for Class 12 Maths in a convenient downloadable PDF format which can be quick and easy to access. These solutions are structured by BYJU’S experts so that they help students remember the crucial points perfectly. This exercise of Chapter 11 Differentiation is mainly focused on the differentiation of inverse trigonometric functions from first principles.
As this is the first exercise of the chapter, students will recall the product rule, quotient rule and differentiation of a constant with an illustration, which was learnt in the previous year. Students can download the PDF of RD Sharma Solutions for Class 12 Exercise 11.1 of Chapter 11 Differentiation from the links provided below.
RD Sharma Solutions for Class 12 Differentiation Exercise 11.1:
Access other exercises of RD Sharma Solutions For Class 12 Chapter 11 – Differentiation
Access answers to Maths RD Sharma Solutions For Class 12 Chapter 11 – Differentiation Exercise 11.1
Exercise 11.1 Page No: 11.17
Differentiate the following functions from the first principles:
1. e-x
Solution:

2. e3x
Solution:

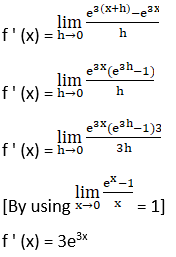
3. eax + b
Solution:

4. ecos x
Solution:
We have to find the derivative of ecos x with the first principle method,
So, let f (x) = ecos x
By using the first principle formula, we get,

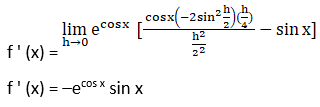
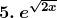
Solution:





Comments