RD Sharma Solutions for Class 12 Maths Chapter 19 Indefinite Integrals

RD Sharma Solutions for Class 12 Maths Chapter 19 – Free PDF Download

RD Sharma Solutions for Class 12 Maths Chapter 19 – Indefinite Integrals is given here. Solving exercise-wise problems using RD Sharma Solutions for Class 12 daily helps students improve their problem-solving and logical thinking skills, which are vital to achieve a better academic score. The main aim is to help students self analyse the areas which require more practice from the exam perspective. With the help of RD Sharma Solutions, students can now solve the exercise problems in a shorter duration with a clear idea about the concepts.

The 19^th Chapter, Indefinite Integrals of RD Sharma Solutions for Class 12 Maths explains some standard results on integration along with fundamental integration formulae.  The RD Sharma Solutions for Class 12 are formulated by BYJU’S experts to provide a fundamental aspect of Maths, which in turn, assists students to understand every concept clearly. The solutions PDF is a major reference guide to help students score well in the Class 12 examination.

RD Sharma Solutions for Class 12 Maths Chapter 19 Indefinite Integrals

Download PDF

carouselExampleControls112

Previous





Next

Access answers to Maths RD Sharma Solutions For Class 12 Chapter 19 – Indefinite Integrals

Exercise 19.1 Page No: 19.4

1. Evaluate the following integrals:

Solution:

Given

Solution:

Given

Solution:

Given

Solution:

Given

Solution:

Given

Solution:

Given

Solution:

Given

Solution:

Given

2. Evaluate:

Solution:

Given

Solution:

Given

3. Evaluate:

Solution:

Given

Exercise 19.2 Page No: 19.14

Evaluate the following integrals (1 – 44):

Solution:

Solution:

Given

Solution:

Given

Solution:

Given,

∫(2 – 3x)(3 + 2x)(1 – 2x) dx

= ∫(6 + 4x – 9x – 6x²)(1 – 2x) dx

= ∫(6 – 5x – 6x²)(1 – 2x) dx

= ∫(6 – 5x – 6x² – 12x + 10x² + 12x³) dx

= ∫(6 – 17x + 4x² + 12x³) dx

Upon splitting the above, we have

= ∫6 dx – ∫17x dx + ∫4x² dx + ∫12x³ dx

On integrating using formula,

∫xⁿ dx = xⁿ⁺¹/n+1

we get

= 6x – 17/(1+1) x¹⁺¹ + 4/(2+1) x²⁺¹ + 12/(3+1) x³⁺¹ + c

= 6x – 17x²/2 + 4x³/3 + 3x⁴ + c

Solution:

Given

Solution:

Solution:

Given

Solution:

Given

Solution:

Solution:

Given

Solution:

Given

Solution:

Solution:

Given

Solution:

Given

Solution:

Given

Solution:

Given

Exercise 19.3 Page No: 19.23

Solution:

Solution:

Solution:

Solution:

Solution:

Solution:

Solution:

Solution:

Solution:

Exercise 19.4 Page No: 19.30

Solution:

Solution:

Solution:

Exercise 19.5 Page No: 19.33

Solution:

Given

Solution:

Solution:

Solution:

Solution:

Exercise 19.6 Page No: 19.36

Solution:

Solution:

Solution:

Solution:

Exercise 19.7 Page No: 19.38

Integrate the following integrals:

Solution:

Solution:

Solution:

Exercise 19.8 Page No: 19.47

Evaluate the following integrals:

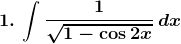
Solution:

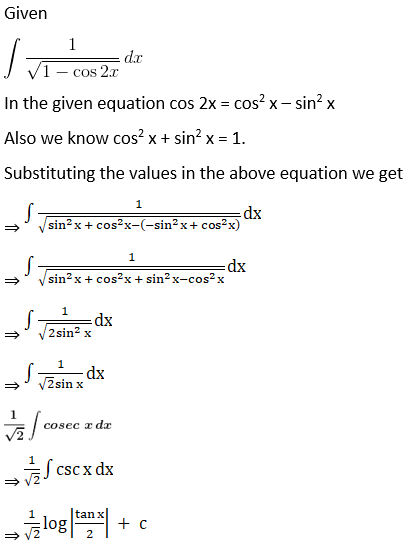
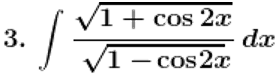
Solution:

Given,

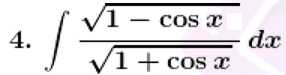
Solution:

Given,

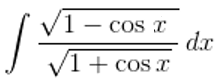
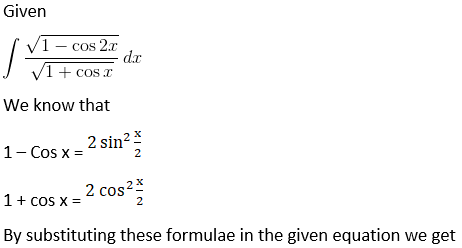
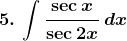
Solution:

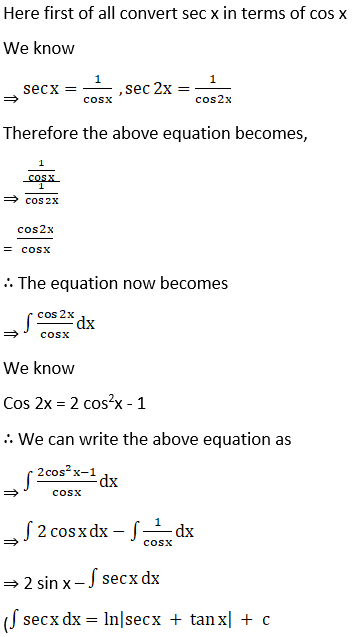
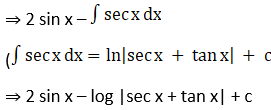
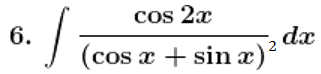
Solution:

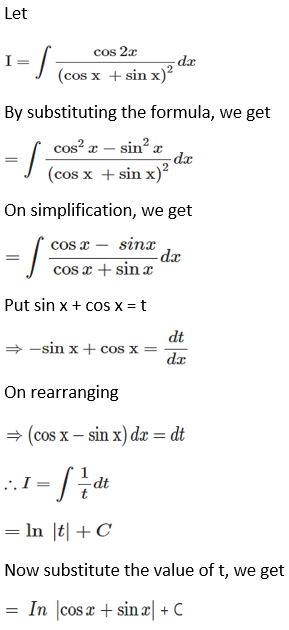
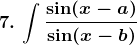
Solution:

Therefore,

= cos (b – a)x + sin(b – a) log |sin(x – b)| + c, where c is an arbitrary constant.

Exercise 19.9 Page No: 19.57

Evaluate the following integrals:

dx

Solution:

Solution:

Solution:

Solution:

Solution:

Solution:

Solution:

Solution:

Solution:

Solution:

Exercise 19.10 Page No: 19.65

Solution:

Solution:

Solution:

Solution:

Solution:

Exercise 19.11 Page No: 19.69

Evaluate the following integrals:

Solution:

Solution:

Solution:

Solution:

Solution:

Solution:

Exercise 19.12 Page No: 19.73

Solution:

Solution:

Solution:

Solution:

Solution:

Exercise 19.13 Page No: 19.79

Solution:

Solution:

Exercise 19.14 Page No: 19.83

Evaluate the following integrals:

Solution:

Solution:

Solution:

Solution:

Solution:

Exercise 19.15 Page No: 19.86

Solution:

Solution:

Solution:

By using,

Solution:

Solution:

Exercise 19.16 Page No: 19.90

Evaluate the following integrals:

Solution:

Solution:

Solution:

Solution:

Solution:

Exercise 19.17 Page No: 19.93

Evaluate the following integrals:

Solution:

Solution:

Solution:

Solution:

Exercise 19.18 Page No: 19.98

Evaluate the following integrals:

Solution:

Solution:

Solution:

Solution:

Let sin x = t

Solution:

Solution:

Solution:

Solution:

Exercise 19.19 Page No: 19.104

Evaluate the following integrals:

Solution:

We will solve I₁ and I₂ individually.

Solution:

Solution:

Solution:

Solution:

Exercise 19.20 Page No: 19.106

Evaluate the following integrals:

Solution:

Solution:

⇒ 1 = (A + B) x + (3A – 2B)

⇒ Then A + B = 0 … (1)

And 3A – 2B = 1 … (2)

Solving (1) and (2),

2 × (1) → 2A + 2B = 0

1 × (2) → 3A – 2B = 1

5A = 1

∴ A = 1/5

Substituting A value in (1),

Or I = log|(x – 2)/(x + 3)| + x + c

Solution:

Solution:

Solution:

Hence,

Exercise 19.21 Page No: 19.110

Evaluate the following integrals:

Solution:

Solution:

Solution:

Solution:

Solution:

Exercise 19.22 Page No: 19.114

Evaluate the following integrals:

Solution:

Solution:

Solution:

Solution:

Exercise 19.23 Page No: 19.117

Evaluate the following integrals:

Solution:

Solution:

Solution:

Solution:

5.

Solution:

Exercise 19.24 Page No: 19.122

Evaluate the following integrals:

Solution:

Solution:

Solution:

Solution:

Solution:

Exercise 19.25 Page No: 19.133

Evaluate the following integrals:

Solution:

Solution:

Solution:

Solution:

Solution:

Exercise 19.26 Page No: 19.143

Evaluate the following integrals:

Solution:

Solution:

Solution:

Solution:

Solution:

Exercise 19.27 Page No: 19.149

Evaluate the following integrals:

Solution:

Solution:

Solution:

Solution:

Solution:

Exercise 19.28 Page No: 19.154

Evaluate the following integrals:

Solution:

Solution:

Solution:

Solution:

Solution:

Exercise 19.29 Page No: 19.158

Evaluate the following integrals:

Solution:

Solution:

Solution:

Solution:

Exercise 19.30 Page No: 19.176

Evaluate the following integrals:

Solution:

Solution:

Solution:

Solution:

Solution:

Exercise 19.31 Page No: 19.190

Evaluate the following integrals:

Solution:

The given equation can be written as,

Solution:

Now, substituting t as x – 1/x and z as x + 1/x we have

Solution:

Solution:

We get,

Solution:

Exercise 19.32 Page No: 19.196

Evaluate the following integrals:

Solution:

Solution:

Solution:

Solution:

Solution:

Access all the exercises of RD Sharma Solutions for Class 12 Chapter 19 – Indefinite Integrals

Exercise 19.1 Solutions

Exercise 19.2 Solutions

Exercise 19.3 Solutions

Exercise 19.4 Solutions

Exercise 19.5 Solutions

Exercise 19.6 Solutions

Exercise 19.7 Solutions

Exercise 19.8 Solutions

Exercise 19.9 Solutions

Exercise 19.10 Solutions

Exercise 19.11 Solutions

Exercise 19.12 Solutions

Exercise 19.13 Solutions

Exercise 19.14 Solutions

Exercise 19.15 Solutions

Exercise 19.16 Solutions

Exercise 19.17 Solutions

Exercise 19.18 Solutions

Exercise 19.19 Solutions

Exercise 19.20 Solutions

Exercise 19.21 Solutions

Exercise 19.22 Solutions

Exercise 19.23 Solutions

Exercise 19.24 Solutions

Exercise 19.25 Solutions

Exercise 19.26 Solutions

Exercise 19.27 Solutions

Exercise 19.28 Solutions

Exercise 19.29 Solutions

Exercise 19.30 Solutions

Exercise 19.31 Solutions

Exercise 19.32 Solutions

RD Sharma Class 12 Maths Solutions Chapter 19 Indefinite Integrals

Some of the essential topics covered in this chapter are listed below.

• Definition of primitive or antiderivative
• Definition and meaning of indefinite integral
• Fundamental integration formulae
• Some standard results on integration along with the corollary
• Integration of trigonometric functions
• Integration of exponential functions
• Miscellaneous problems
• Geometrical interpretation of indefinite integral
• Comparison between differentiation and integration
• Methods of integration
• Integration by substitution
• Some standard results
• Evaluation of integrals by using trigonometric substitutions
• Some special integrals
• Integration by parts
• Some important integrals along with theorems
• Integration of rational algebraic functions by using partial fractions
  • When the denominator is expressible as a product of distinct linear factors
  • When the denominator contains some repeating linear factors
  • The denominator contains irreducible quadratic factors
• Integration of some special irrational algebraic functions