RD Sharma Solutions for Class 12 Maths Chapter 16 Tangents and Normals

RD Sharma Solutions for Class 12 Maths Chapter 16 – Free PDF Download (Updated for 2023-24)

RD Sharma Solutions for Class 12 Chapter 16 – Tangents and Normals are provided here for students to learn the concepts better. According to the CBSE syllabus, RD Sharma is the best book for practising Class 12 Maths. Therefore, it is clear that students who aim to excel in Maths should refer to RD Sharma Solutions for Class 12. Our experts have created these RD Sharma Solutions with utmost precision to help students in their studies. The description provided in the PDFs enhances the students’ basic concepts, which in turn aids in solving problems without making any mistakes.

The 16th Chapter of RD Sharma Solutions  Class 12 Tangents and Normals explains slopes of tangents and normals as its primary concept. By practising these solutions, students can score high marks in their academic examinations. The RD Sharma Class 12 Solutions Chapter 16 PDF is available for free download through the links provided below.

RD Sharma Solutions Class 12 Maths Chapter 16 Tangents and Normals:

Download PDF

carouselExampleControls112

Previous Next

Access answers to Maths RD Sharma Solutions For Class 12 Chapter 16 – Tangents and Normals

Exercise 16.1 Page No: 16.10

1. Find the Slopes of the tangent and the normal to the following curves at the indicated points:

Solution:

(ii) y = √x at x = 9

Solution:

⇒ The Slope of the normal = – 6

(iii) y = x³ – x at x = 2

Solution:

(iv) y = 2x² + 3 sin x at x = 0

Solution:

(v) x = a (θ – sin θ), y = a (1 + cos θ) at θ = -π /2

Solution:

(vi) x = a cos³ θ, y = a sin³ θ at θ = π /4

Solution:

(vii) x = a (θ – sin θ), y = a (1 – cos θ) at θ = π /2

Solution:

(viii) y = (sin 2x + cot x + 2)² at x = π /2

Solution:

(ix) x² + 3y + y² = 5 at (1, 1)

Solution:

(x) x y = 6 at (1, 6)

Solution:

2. Find the values of a and b if the Slope of the tangent to the curve x y + a x + by = 2 at (1, 1) is 2.

Solution:

⇒ – a – 1 = 2(1 + b)

⇒ – a – 1 = 2 + 2b

⇒ a + 2b = – 3 … (1)

Also, the point (1, 1) lies on the curve xy + ax + by = 2, we have

1 × 1 + a × 1 + b × 1 = 2

⇒ 1 + a + b = 2

⇒ a + b = 1 … (2)

From (1) & (2), we get b = -4

Substitute b = – 4 in a + b = 1

a – 4 = 1

⇒ a = 5

So the value of a = 5 & b = – 4

3. If the tangent to the curve y = x³ + a x + b at (1, – 6) is parallel to the line x – y + 5 = 0, find a and b

Solution:

The given line is x – y + 5 = 0

y = x + 5 is the form of equation of a straight line y = mx + c, where m is the Slope of the line.

So the slope of the line is y = 1 × x + 5

So the Slope is 1. … (2)

Also the point (1, – 6) lie on the tangent, so

x = 1 & y = – 6 satisfies the equation, y = x³ + ax + b

– 6 = 1³ + a × 1 + b

⇒ – 6 = 1 + a + b

⇒ a + b = – 7 … (3)

Since, the tangent is parallel to the line, from (1) & (2)

Hence, 3 + a = 1

⇒ a = – 2

From (3)

a + b = – 7

⇒ – 2 + b = – 7

⇒ b = – 5

So the value is a = – 2 & b = – 5

4. Find a point on the curve y = x³ – 3x where the tangent is parallel to the chord joining (1, – 2) and (2, 2).

Solution:

5. Find a point on the curve y = x³ – 2x² – 2x at which the tangent lines are parallel to the line y = 2x – 3.

Solution:

Given the curve y = x³ – 2x² – 2x and a line y = 2x – 3

First, we will find the slope of tangent

y = x³ – 2x² – 2x

y = 2x – 3 is the form of equation of a straight line y = mx + c, where m is the Slope of the line.

So the slope of the line is y = 2 × (x) – 3

Thus, the Slope = 2. … (2)

From (1) & (2)

⇒ 3x² – 4x – 2 = 2

⇒ 3x² – 4x = 4

⇒ 3x² – 4x – 4 = 0

We will use factorization method to solve the above Quadratic equation.

⇒ 3x² – 6x + 2x – 4 = 0

⇒ 3 x (x – 2) + 2 (x – 2) = 0

⇒ (x – 2) (3x + 2) = 0

⇒ (x – 2) = 0 & (3x + 2) = 0

⇒ x = 2 or

x = -2/3

Substitute x = 2 & x = -2/3 in y = x³ – 2x² – 2x

When x = 2

⇒ y = (2)³ – 2 × (2)² – 2 × (2)

⇒ y = 8 – (2 × 4) – 4

⇒ y = 8 – 8 – 4

⇒ y = – 4

6. Find a point on the curve y² = 2x³ at which the Slope of the tangent is 3

Solution:

Given the curve y² = 2x³ and the Slope of tangent is 3

y² = 2x³

Differentiating the above with respect to x

dy/dx = 0 which is not possible.

So we take x = 2 and substitute it in y² = 2x³, we get

y² = 2(2)³

y² = 2 × 8

y² = 16

y = 4

Thus, the required point is (2, 4)

7. Find a point on the curve x y + 4 = 0 at which the tangents are inclined at an angle of 45^o with the x–axis.

Solution:

Substitute in xy + 4 = 0, we get

⇒ x (– x) + 4 = 0

⇒ – x² + 4 = 0

⇒ x² = 4

⇒ x =
2

So when x = 2, y = – 2

And when x = – 2, y = 2

Thus, the points are (2, – 2) & (– 2, 2)

8. Find a point on the curve y = x² where the Slope of the tangent is equal to the x – coordinate of the point.

Solution:

Given the curve is y = x²

y = x²

Differentiating the above with respect to x

From (1) & (2), we get,

2x = x

⇒ x = 0.

Substituting this in y = x², we get,

y = 0²

⇒ y = 0

Thus, the required point is (0, 0)

9. At what point on the circle x² + y² – 2x – 4y + 1 = 0, the tangent is parallel to x – axis.

Solution:

⇒ – (x – 1) = 0

⇒ x = 1

Substituting x = 1 in x² + y² – 2x – 4y + 1 = 0, we get,

⇒ 1² + y² – 2(1) – 4y + 1 = 0

⇒ 1 – y² – 2 – 4y + 1 = 0

⇒ y² – 4y = 0

⇒ y (y – 4) = 0

⇒ y = 0 and y = 4

Thus, the required point is (1, 0) and (1, 4)

10. At what point of the curve y = x² does the tangent make an angle of 45^o with the x–axis?

Solution:

Given the curve is y = x²

Differentiating the above with respect to x

⇒ y = x²

Exercise 16.2 Page No: 15.27

1. Find the equation of the tangent to the curve √x + √y = a, at the point (a²/4, a²/4).

Solution:

2. Find the equation of the normal to y = 2x³ – x² + 3 at (1, 4).

Solution:

3. Find the equation of the tangent and the normal to the following curves at the indicated points:

(i) y = x⁴ – 6x³ + 13x² – 10x + 5 at (0, 5)

Solution:

(ii) y = x⁴ – 6x³ + 13x² – 10x + 5 at x = 1 y = 3

Solution:

(iii) y = x² at (0, 0)

Solution:

Given y = x² at (0, 0)

By differentiating the given curve, we get the slope of the tangent

m (tangent) at (x = 0) = 0

Normal is perpendicular to tangent so, m₁m₂ = – 1

We can see that the slope of normal is not defined

Equation of tangent is given by y – y₁ = m (tangent) (x – x₁)

y = 0

Equation of normal is given by y – y₁ = m (normal) (x – x₁)

x = 0

(iv) y = 2x² – 3x – 1 at (1, – 2)

Solution:

Given y = 2x² – 3x – 1 at (1, – 2)

By differentiating the given curve, we get the slope of the tangent

m (tangent) at (1, – 2) = 1

Normal is perpendicular to tangent so, m₁m₂ = – 1

m (normal) at (1, – 2) = – 1

Equation of tangent is given by y – y₁ = m (tangent) (x – x₁)

y + 2 = 1(x – 1)

y = x – 3

Equation of normal is given by y – y₁ = m (normal) (x – x₁)

y + 2 = – 1(x – 1)

y + x + 1 = 0

Solution:

Equation of tangent is given by y – y₁ = m (tangent) (x – x₁)

y + 2 = – 2(x – 2)

y + 2x = 2

Equation of normal is given by y – y₁ = m (normal) (x – x₁)

2y + 4 = x – 2

2y – x + 6 = 0

4. Find the equation of the tangent to the curve x = θ + sin θ, y = 1 + cos θ at θ = π/4.

Solution:

5. Find the equation of the tangent and the normal to the following curves at the indicated points:

(i) x = θ + sin θ, y = 1 + cos θ at θ = π/2

Solution:

Given x = θ + sin θ, y = 1 + cos θ at θ = π/2

By differentiating the given equation with respect to θ, we get the slope of the tangent

Solution:

(iii) x = at², y = 2at at t = 1.

Solution:

(iv) x = a sec t, y = b tan t at t.

Solution:

(v) x = a (θ + sin θ), y = a (1 – cos θ) at θ

Solution:

(vi) x = 3 cos θ – cos³ θ, y = 3 sin θ – sin³θ

Solution:

6. Find the equation of the normal to the curve x² + 2y² – 4x – 6y + 8 = 0 at the point whose abscissa is 2.

Solution:

Finding y co – ordinate by substituting x in the given curve

2y² – 6y + 4 = 0

y² – 3y + 2 = 0

y = 2 or y = 1

m (tangent) at x = 2 is 0

Normal is perpendicular to tangent so, m₁m₂ = – 1

m (normal) at x = 2 is 1/0, which is undefined

Equation of normal is given by y – y₁ = m (normal) (x – x₁)

x = 2

7. Find the equation of the normal to the curve ay² = x³ at the point (am², am³).

Solution:

8. The equation of the tangent at (2, 3) on the curve y² = ax³ + b is y = 4x – 5. Find the values of a and b.

Solution:

Given y² = ax³ + b is y = 4x – 5

By differentiating the given curve, we get the slope of the tangent

m (tangent) at (2, 3) = 2a

Equation of tangent is given by y – y₁ = m (tangent) (x – x₁)

Now comparing the slope of a tangent with the given equation

2a = 4

a = 2

Now (2, 3) lies on the curve, these points must satisfy

3² = 2 × 2³ + b

b = – 7

9. Find the equation of the tangent line to the curve y = x² + 4x – 16 which is parallel to the line 3x – y + 1 = 0.

Solution:

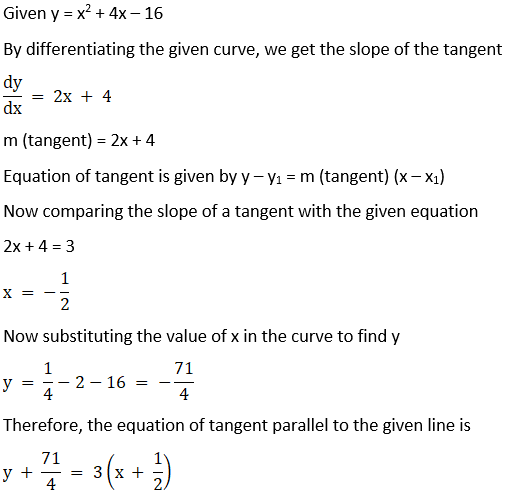
10. Find the equation of normal line to the curve y = x³ + 2x + 6 which is parallel to the line x + 14y + 4 = 0.

Solution:

Exercise 16.3 Page No: 16.40

1. Find the angle to intersection of the following curves:

(i) y² = x and x² = y

Solution:

x = y²

When y = 0, x = 0

When y = 1, x = 1

Substituting above values for m₁ & m_2, we get,

When x = 0,

(ii) y = x² and x² + y² = 20

Solution:

(iii) 2y² = x³ and y² = 32x

Solution:

Substituting (2) in (1), we get

⇒ 2y² = x³

⇒ 2(32x) = x³

⇒ 64 x = x³

⇒ x³ – 64x = 0

⇒ x (x² – 64) = 0

⇒ x = 0 & (x² – 64) = 0

⇒ x = 0 & ±8

Substituting x = 0 & x = ±8 in (1) in (2),

y² = 32x

When x = 0, y = 0

When x = 8

⇒ y² = 32 × 8

⇒ y² = 256

⇒ y = ±16

Substituting above values for m₁ & m_2, we get,

When x = 0, y = 16

(iv) x² + y² – 4x – 1 = 0 and x² + y² – 2y – 9 = 0

Solution:

Given curves x² + y² – 4x – 1 = 0 … (1) and x² + y² – 2y – 9 = 0 … (2)

First curve is x² + y² – 4x – 1 = 0

⇒ x² – 4x + 4 + y² – 4 – 1 = 0

⇒ (x – 2)² + y² – 5 = 0

Now, Subtracting (2) from (1), we get

⇒ x² + y² – 4x – 1 – ( x² + y² – 2y – 9) = 0

⇒ x² + y² – 4x – 1 – x² – y² + 2y + 9 = 0

⇒ – 4x – 1 + 2y + 9 = 0

⇒ – 4x + 2y + 8 = 0

⇒ 2y = 4x – 8

⇒ y = 2x – 4

Substituting y = 2x – 4 in (3), we get,

⇒ (x – 2)² + (2x – 4)² – 5 = 0

⇒ (x – 2)² + 4(x – 2)² – 5 = 0

⇒ (x – 2)²(1 + 4) – 5 = 0

⇒ 5(x – 2)² – 5 = 0

⇒ (x – 2)² – 1 = 0

⇒ (x – 2)² = 1

⇒ (x – 2) = ±1

⇒ x = 1 + 2 or x = – 1 + 2

⇒ x = 3 or x = 1

So, when x = 3

y = 2×3 – 4

⇒ y = 6 – 4 = 2

So, when x = 3

y = 2 × 1 – 4

⇒ y = 2 – 4 = – 2

The point of intersection of two curves are (3, 2) & (1, – 2)

Solution:

2. Show that the following set of curves intersect orthogonally:
(i) y = x³ and 6y = 7 – x²

Solution:

Given curves y = x³ … (1) and 6y = 7 – x² … (2)

Solving (1) & (2), we get

⇒ 6y = 7 – x²

⇒ 6(x³) = 7 – x²

⇒ 6x³ + x² – 7 = 0

Since f(x) = 6x³ + x² – 7,

We have to find f(x) = 0, so that x is a factor of f(x).

When x = 1

f (1) = 6(1)³ + (1)² – 7

f (1) = 6 + 1 – 7

f (1) = 0

Hence, x = 1 is a factor of f(x).

Substituting x = 1 in y = x³, we get

y = 1³

y = 1

The point of intersection of two curves is (1, 1)

First curve y = x³

Differentiating above with respect to x,

(ii) x³ – 3xy² = – 2 and 3x² y – y³ = 2

Solution:

Given curves x³ – 3xy² = – 2 … (1) and 3x²y – y³ = 2 … (2)

Adding (1) & (2), we get

⇒ x³ – 3xy² + 3x²y – y³ = – 2 + 2

⇒ x³ – 3xy² + 3x²y – y³ = – 0

⇒ (x – y)³ = 0

⇒ (x – y) = 0

⇒ x = y

Substituting x = y on x³ – 3xy² = – 2

⇒ x³ – 3 × x × x² = – 2

⇒ x³ – 3x³ = – 2

⇒ – 2x³ = – 2

⇒ x³ = 1

⇒ x = 1

Since x = y

y = 1

The point of intersection of two curves is (1, 1)

First curve x³ – 3xy² = – 2

Differentiating above with respect to x,

(iii) x² + 4y² = 8 and x² – 2y² = 4.

Solution:

3. x² = 4y and 4y + x² = 8 at (2, 1)

Solution:

(ii) x² = y and x³ + 6y = 7 at (1, 1)

Solution:

Given curves x² = y … (1) and x³ + 6y = 7 … (2)

The point of intersection of two curves (1, 1)

Solving (1) & (2), we get,

First curve is x² = y

Differentiating above with respect to x,

(iii) y² = 8x and 2x² + y² = 10 at (1, 2√2)

Solution:

Given curves y² = 8x … (1) and 2x² + y² = 10 … (2)

4. Show that the curves 4x = y² and 4xy = k cut at right angles, if k² = 512.

Solution:

5. Show that the curves 2x = y² and 2xy = k cut at right angles, if k² = 8.

Solution:

Given curves 2x = y² … (1) and 2xy = k … (2)

We have to prove that two curves cut at right angles if k² = 8

Now, differentiating curves (1) & (2) with respect to x, we get

⇒ 2x = y²

Also, Access RD Sharma Solutions for Class 12 Maths Chapter 16 Tangents and Normals

Exercise 16.1 Solutions

Exercise 16.2 Solutions

Exercise 16.3 Solutions

RD Sharma Class 12 Maths Solutions Chapter 16 Tangents and Normals

Some of the essential topics of this chapter are listed below.

• The slope of a line
• Slopes of tangent and normal
• Finding the slopes of the tangent and the normal at a given point
• Finding the point on a given curve at which tangent is parallel or perpendicular to a given line
• Equations of tangents and normal
• Finding the equations of tangent and normal to a curve at a given point
• Finding tangent and normal parallel or perpendicular to a given line
• Finding tangent or normal passing through a given point
• Miscellaneous applications of tangents and normals
• Finding the equations of tangent and normal
• Finding the equation of the curve
• The angle of intersection of two curves
• Orthogonal curves