RD Sharma Solutions for Class 12 Maths Chapter 11 Differentiation

RD Sharma Solutions for Class 12 Maths Chapter 11 – Free PDF Download Updated for (2023-24)

RD Sharma Solutions for Class 12 Maths Chapter 11 – Differentiation PDF is provided here for students to score good marks in the exams. Students can refer to and download Chapter 11 Differentiation from the given links. These RD Sharma Solutions for Class 12 facilitate students to create good knowledge about basic concepts of CBSE Class 12 Mathematics. This chapter is based on the differentiation of a given function.

RD Sharma books offer several questions for practice at the end of each chapter. RD Sharma Solutions for Class 12 provided here are easily readable and created in such a way to help students clear all their doubts that they might face while answering the given problems in exercises. These RD Sharma Solutions are prepared by experts in Maths at BYJU’S.

Some of the primary topics covered in the RD Sharma Solutions of this chapter are listed below.

• Recapitulation of the product rule, quotient rule and differentiation of a constant with an illustration.
• Differentiation of inverse trigonometric functions from first principles.
• Differentiation of a function of a function.
• Differentiation of inverse trigonometric functions by the chain rule.
• Differentiation by using trigonometrical substitutions.
• Differentiation of implicit functions.
• Logarithmic differentiation.
• Differentiation of infinite series.
• Differentiation of parametric functions.
• Differentiation of a function with respect to another function.
• Differentiation of determinants.

RD Sharma Solutions for Class 12 Maths Chapter 11 Differentiation:

Download PDF

carouselExampleControls111

Previous



Next

Access answers to Maths RD Sharma Solutions For Class 12 Chapter 11 – Differentiation

Exercise 11.1 Page No: 11.17

Differentiate the following functions from the first principles:

1. e^-x

Solution:

2. e^3x

Solution:

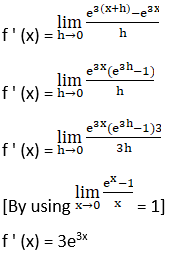
3. e^{ax + b}

Solution:

4. e^{cos x}

Solution:

We have to find the derivative of e^cos x with the first principle method,

So, let f (x) = e^cos x

By using the first principle formula, we get,

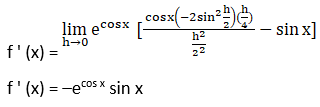
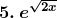
Solution:

Exercise 11.2 Page No: 11.37

Differentiate the following functions with respect to x:

1. Sin (3x + 5)

Solution:

Given Sin (3x + 5)

2. tan² x

Solution:

Given tan² x

3. tan (x^o + 45^o)

Solution:

Let y = tan (x° + 45°)

First, we will convert the angle from degrees to radians.

4. Sin (log x)

Solution:

Given sin (log x)

Solution:

6. e^{tan x}

Solution:

7. Sin² (2x + 1)

Solution:

Let y = sin² (2x + 1)

On differentiating y with respect to x, we get

8. log₇ (2x – 3)

Solution:

9. tan 5x^o

Solution:

Let y = tan (5x°)

First, we will convert the angle from degrees to radians. We have

Solution:

Solution:

12. log_x 3

Solution:

Solution:

Solution:

Solution:

Solution:

Solution:

18. (log sin x)²

Solution:

Let y = (log sin x)²

Solution:

Solution:

21. e^3x cos 2x

Solution:

22. Sin (log sin x)

Solution:

23. e^{tan 3x}

Solution:

Solution:

Solution:

Solution:

27. tan (e^{sin x})

Solution:

Solution:

Solution:

30. log (cosec x – cot x)

Solution:

Solution:

Solution:

33. tan^-1 (e^x)

Solution:

Solution:

35. sin (2 sin^-1 x)

Solution:

Let y = sin (2sin^–1x)

On differentiating y with respect to x, we get

Solution:

Solution:

Exercise 11.3 Page No: 11.62

Differentiate the following functions with respect to x:

Solution:

Solution:

Solution:

Let,

Solution:

Let,

Solution:

Solution:

7. Sin^-1 (2x² – 1), 0 < x < 1

Solution:

8. Sin^-1 (1 – 2x²), 0 < x < 1

Solution:

Solution:

Solution:

Solution:

Solution:

Solution:

Solution:

Solution:

Solution:

Solution:

Solution:

Solution:

Let,

Solution:

Solution:

Solution:

Solution:

Exercise 11.4 Page No: 11.74

Find dy/dx in each of the following:

1. xy = c²

Solution:

2. y³ – 3xy² = x³ + 3x²y

Solution:

Given y³ – 3xy² = x³ + 3x²y,

Now we have to find dy/dx of given equation, so by differentiating the equation on both sides with respect to x, we get,

3. x^2/3 + y^2/3 = a^2/3

Solution:

Given x^2/3 + y^2/3 = a^2/3,

Now we have to find dy/dx of given equation, so by differentiating the equation on both sides with respect to x, we get,

4. 4x + 3y = log (4x – 3y)

Solution:

Given 4x + 3y = log (4x – 3y),

Now we have to find dy/dx of it, so by differentiating the equation on both sides with respect to x, we get,

Solution:

6. x⁵ + y⁵ = 5xy

Solution:

Given x⁵ + y⁵ = 5xy

Now we have to find dy/dx of given equation, so by differentiating the equation on both sides with respect to x, we get,

7. (x + y)² = 2axy

Solution:

Given (x + y)² = 2axy

Now we have to find dy/dx of given equation, so by differentiating the equation on both sides with respect to x, we get,

8. (x² + y²)² = xy

Solution:

Given (x + y)² = 2axy

Now we have to find dy/dx of given equation, so by differentiating the equation on both sides with respect to x, we get,

9. Tan^-1 (x² + y²)

Solution:

Given tan ^{– 1}(x² + y²) = a,

Now we have to find dy/dx of given function, so by differentiating the equation on both sides with respect to x, we get,

Solution:

11. Sin xy + cos (x + y) = 1

Solution:

Given Sin x y + cos (x + y) = 1

Now we have to find dy/dx of given function, so by differentiating the equation on both sides with respect to x, we get,

Solution:

Solution:

Solution:

Solution:

Exercise 11.5 Page No: 11.88

Differentiate the following functions with respect to x:

1. x^1/x

Solution:

2. x^{sin x}

Solution:

3. (1 + cos x)^x

Solution:

Solution:

5. (log x)^x

Solution:

6. (log x)^{cos x}

Solution:

Let y = (log x)^{cos x}

Taking log both the sides, we get

7. (Sin x)^{cos x}

Solution:

8. e^{x log x}

Solution:

9. (Sin x)^{log x}

Solution:

10. 10^{log sin x}

Solution:

11. (log x)^{log x}

Solution:

Solution:

13. Sin (x^x)

Solution:

14. (Sin^-1 x)^x

Solution:

Solution:

16. (tan x)^1/x

Solution:

Solution:

18. (i) (x^x) √x

Solution:

Solution:

Solution:

Solution:

Solution:

18. (vi) e^{sin x} + (tan x)^x

Solution:

18. (vii) (cos x)^x + (sin x)^1/x

Solution:

Solution:

19. y = e^x + 10^x + x^x

Solution:

20. y = xⁿ + n^x + x^x + nⁿ

Solution:

Exercise 11.6 Page No: 11.98

Solution:

Solution:

Solution:

Solution:

Exercise 11.7 Page No: 11.103

Find dy/dx, when

1. x = at² and y = 2 at

Solution:

2. x = a (θ + sin θ) and y = a (1 – cos θ)

Solution:

3. x = a cos θ and y = b sin θ

Solution:

Given x = a cos θ and y = b sin θ

4. x = a e^θ (sin θ – cos θ), y = a e^θ (sin θ + cos θ)

Solution:

5. x = b sin² θ and y = a cos² θ

Solution:

6. x = a (1 – cos θ) and y = a (θ + sin θ) at θ = π/2

Solution:

Solution:

Solution:

9. x = a (cos θ + θ sin θ) and y = a (sin θ – θ cos θ)

Solution:

Solution:

Solution:

Solution:

Solution:

Solution:

Exercise 11.8 Page No: 11.112

1. Differentiate x² with respect to x³.

Solution:

2. Differentiate log (1 +x²) with respect to tan^-1 x.

Solution:

3. Differentiate (log x)^x with respect to log x.

Solution:

4. Differentiate sin^-1 √ (1-x²) with respect to cos^-1x, if

(i) x ∈ (0, 1)

(ii) x ∈ (-1, 0)

Solution:

(i) Given sin^-1 √ (1-x²)

(ii) Given sin^-1 √ (1-x²)

Solution:

(i) Let

(ii) Let

(iii) Let

Solution:

(i) x ∈ (0, 1/ √2)

(ii) x ∈ (1/√2, 1)

Solution:

(i) Let

(ii) Let

8. Differentiate (cos x)^{sin x} with respect to (sin x)^{cos x}.

Solution:

Solution:

Solution:

Also, Access RD Sharma Solutions for Class 12 Maths Chapter 11 Differentiation

Exercise 11.1 Solutions

Exercise 11.2 Solutions

Exercise 11.3 Solutions

Exercise 11.4 Solutions

Exercise 11.5 Solutions

Exercise 11.6 Solutions

Exercise 11.7 Solutions

Exercise 11.8 Solutions