In Exercise 19.1 of Chapter 19, we shall discuss some polyhedrons (a solid shape bounded by polygons is termed a polyhedron). We shall also study prisms and pyramids and their types. Solutions are designed by our subject experts with explanations in simple language to help students understand the problems and concepts in the chapter. Students can improve their problem-solving ability by practising the problems provided in the RD Sharma Class 8 Solutions, which are very beneficial during their exam preparation. Besides, they can download the PDF from the available links given below.
RD Sharma Solutions for Class 8 Maths Exercise 19.1 Chapter 19 Visualising Shapes
Access answers to RD Sharma Maths Solutions for Class 8 Exercise 19.1 Chapter 19 Visualising Shapes
1. What is the least number of planes that can enclose a solid? What is the name of the solid?
Solution:
The least number of planes that are required to enclose a solid is 4.
The name of solid is tetrahedron.
2. Can a polyhedron have for its faces?
(i) 3 triangles?
(ii) 4 triangles?
(iii) a square and four triangles?
Solution:
(i) 3 triangles?
No, because a polyhedron is a solid shape bounded by polygons.
(ii) 4 triangles?
Yes, because a tetrahedron as 4 triangles as its faces.
(iii) a square and four triangles?
Yes, because a square pyramid has a square and four triangles as its faces.
3. Is it possible to have a polyhedron with any given number of faces?
Solution:
Yes, if number of faces is four or more.
4. Is a square prism same as a cube?
Solution:
Yes. We know that a square is a three dimensional shape with six rectangular shaped sides, out of which two are squares. Cubes are of rectangular prism length, width and height of same measurement.
5. Can a polyhedron have 10 faces, 20 edges and 15 vertices?
Solution:
No.
Let us use Euler’s formula
V + F = E + 2
15 + 10 = 20 + 2
25 ≠ 22
Since the given polyhedron is not following Euler’s formula, therefore it is not possible to have 10 faces, 20 edges and 15 vertices.
6. Verify Euler’s formula for each of the following polyhedrons:
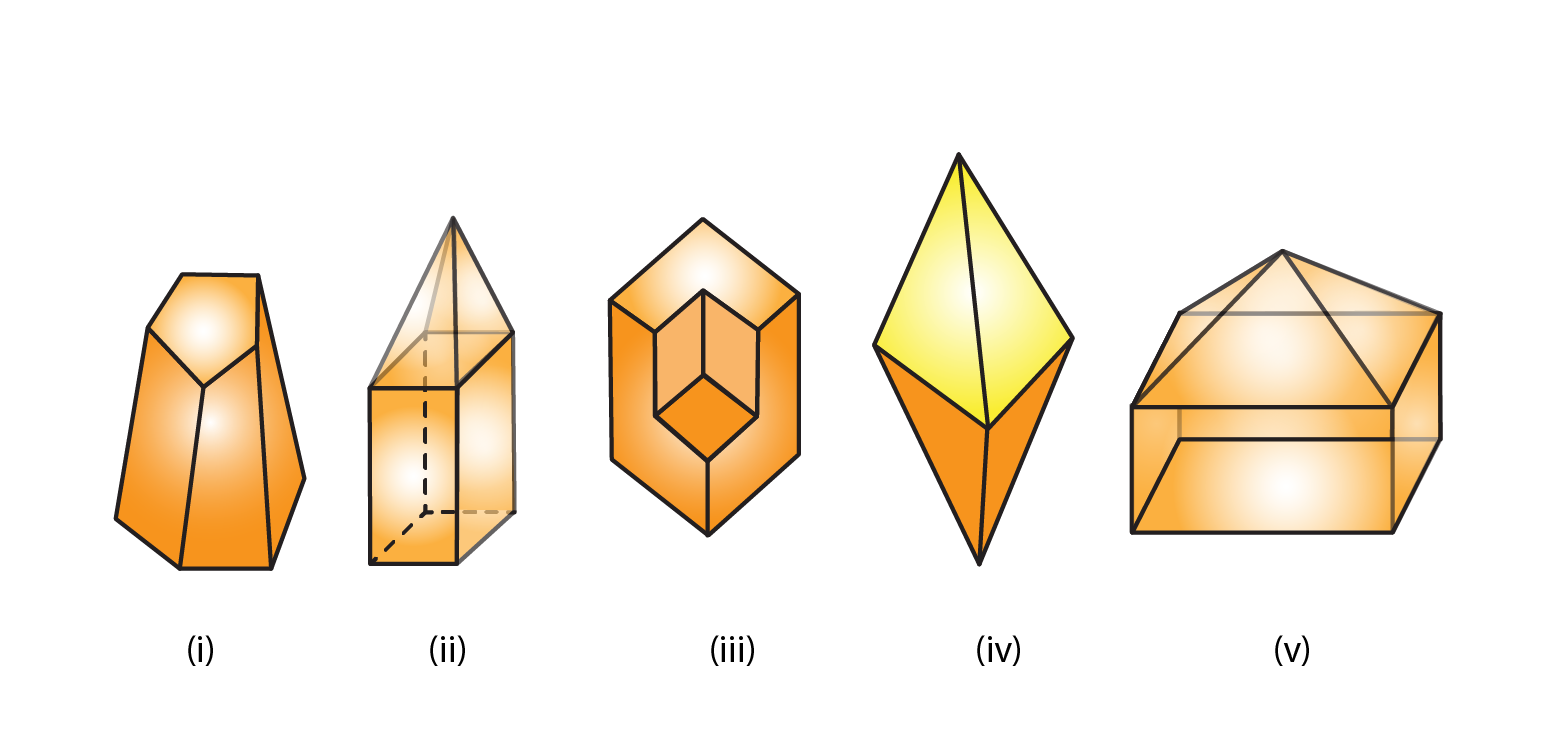
Solution:
(i) Vertices = 10
Faces = 7
Edges = 15
By using Euler’s formula
V + F = E + 2
10 + 7 = 15 + 2
17 = 17
Hence verified.
(ii) Vertices = 9
Faces = 9
Edges = 16
By using Euler’s formula
V + F = E + 2
9 + 9 = 16 + 2
18 = 18
Hence verified.
(iii) Vertices = 14
Faces = 8
Edges = 20
By using Euler’s formula
V + F = E + 2
14 + 8 = 20 + 2
22 = 22
Hence verified.
(iv) Vertices = 6
Faces = 8
Edges = 12
By using Euler’s formula
V + F = E + 2
6 + 8 = 12 + 2
14 = 14
Hence verified.
(v) Vertices = 9
Faces = 9
Edges = 16
By using Euler’s formula
V + F = E + 2
9 + 9 = 16 + 2
18 = 18
Hence verified.
7. Using Euler’s formula find the unknown:
| Faces | ? | 5 | 20 |
| Vertices | 6 | ? | 12 |
| Edges | 12 | 9 | ? |
Solution:
(i)
By using Euler’s formula
V + F = E + 2
6 + F = 12 + 2
F = 14 – 6
F = 8
∴ Number of faces is 8
(ii)
By using Euler’s formula
V + F = E + 2
V + 5 = 9 + 2
V = 11 – 5
V = 6
∴ Number of vertices is 6
(iii)
By using Euler’s formula
V + F = E + 2
12 + 20 = E + 2
E = 32 – 2
E = 30
∴ Number of edges is 30




Comments