Basic geometrical ideas Class 6 notes covers all the important concepts included in this chapter, along with examples and practice questions. These CBSE class 6 chapter 4 notes will not only help the students to learn the concepts more easily but will also help them to revise this chapter more effectively.
Introduction to Basic Geometrical Ideas
In this chapter, several important geometric terms are included, which hold extreme importance in higher classes. The topics that are introduced will not only help students to build a foundation in geometry but will also help them to grasp the higher-level concepts in the later grades easily.
The main topics covered here are-
- Basic Definitions in Geometry
- Polygons
- Triangles
- Quadrilaterals
- About Circles
Basic Definitions in Geometry
| Terms | Definition |
| Point | It determines a location and is usually determined by a capital letter. |
| Line segment | The shortest distance between two points is called a line segment. |
| Line | By extending a line segment indefinitely on both sides, a line is obtained. |
| Intersecting lines | If two distinct lines meet or cross at a point, they are called intersecting lines. |
| Parallel lines | Parallel lines are lines which are always the same distance apart and never intersect anywhere in a plane. |
| Ray | A ray is a line which starts from a particular point and goes infinitely towards a particular direction. |
| Curve | It is a drawing which is done without lifting the pencil. |
| Simple curve | A curve that never crosses itself is a simple curve. |
| Closed and open curves | A curve is closed if its ends are joined. Otherwise, it is an open curve. |
| Angle | It is made up of two rays which are starting from a common point. |
Polygons
A polygon can be defined as a closed curve which is made up of line segments. Polygons can be of numerous types, like triangles (having 3 line segments), quadrilaterals (having 4 line segments), pentagons (having 5 line segments), and so on. A few important terms related to polygons are-
| Terms | Definition |
| Sides of a polygon | The line segments are known as the sides of the polygon. |
| Adjacent sides | Two points having the same endpoint are called adjacent sides. |
| Vertex | Vertex is the meeting or intersecting point of a pair of sides. |
| Diagonal | Diagonal is obtained by joining any two non-adjacent vertices of a polygon. |
To know more about Polygon, visit here.
Triangles
A triangle is as a polygon having three line segments or sides. A triangle ABC is written as
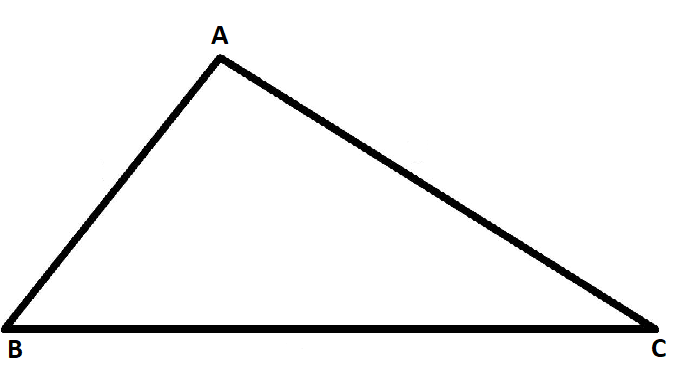
In this triangle, AB, BC, and AC are sides of the triangle and A, B, C are the vertices of the triangle. Also, the angle between BC and AB is the
For more information on Triangles, watch the below video

To know more about Triangles, visit here.
Quadrilaterals
A quadrilateral is defined as a four-sided polygon, i.e., having 4 line segments or sides and, thus, 4 angles. The diagram of a quadrilateral is given for better understanding. It should be noted that the vertices of a quadrilateral are named in a cyclic manner.
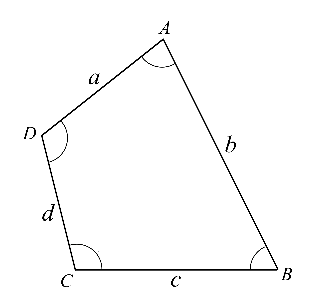
In this diagram, AD and DC are one of examples of adjacent sides. Also, AD and BC are one of the opposite sides. Here, angle A and angle C are opposite angles. In this, if the line segment is drawn from A to C or from B to D, it becomes a diagonal.
For more information on Quadrilaterals, Watch The Below Video.

To know more about Quadrilaterals, visit here.
About Circles
A circle can be defined as a closed figure formed by a set of points in a plane which are located at the same distance from a fixed point which is the centre. A few important terms related to circles are-
| Terms | Definitions |
| Radius | The fixed distance at which the points are located from the centre is called the radius. |
| Diameter | Diameter is the length of a line segment which joins any two points on the circle by passing through the centre. Diameter is always double than the radius. |
| Circumference | The distance around the circle is known as its circumference or perimeter. |
| Chord | A line segment joining any two points on the circle is a chord. |
| Sector | It is the region in the interior of a circle which is enclosed by an arc on one side and a pair of radii on the other two sides. |
| Segment | It is a region in the interior of the circle enclosed by an arc and a chord. |
For more information on Circles, watch the below video


To know more about Circles, visit here.
Points
- A point determines a specific location.
- They are denoted by any capital letter of the English Alphabet.
Curves
- In simple terms, any line that is not straight is said to be a curve.
- If a curve does not cross itself, then it is called a simple curve.

Closed and Open Curves
- A curve is said to be closed if its ends are joined.
- A curve whose ends are opened is said to be an open curve.

Polygons
A simple closed figure made up of line segments is called a polygon.
Terms Related to Polygons
Some of the important terms related to a polygon are :


- Vertex: The meeting point of a pair of sides. Here A, B, C, D and E are the vertices of the polygon.
- Adjacent sides: Any two sides of a polygon with a common endpoint. Here AB and BC are adjacent sides.
- Adjacent vertices: Endpoints of the same side of a polygon. Here A and B are the adjacent vertices.
- Diagonals: The lines joining the non-adjacent vertices of a polygon. Here AC, AD, BD, BE and CE are the diagonals.
For more information on Introduction to Geometry and Polygons, watch the below video

Triangle
- A triangle is a three-sided polygon.
- It has three sides, three angles and three vertices.
- It has an interior and exterior region.

In the above figure:

Quadrilaterals
- A quadrilateral is a four-sided polygon with four sides, four angles and four vertices.

In a quadrilateral ABCD:
- AB, BC, CD and DA are the sides of the quadrilateral.
- A, B, C and D are the vertices.
- AB and CD, and BC and DA are the pairs of opposite sides.
- Angle A and angle C, and angles B and D are the pairs of opposite angles.
- Angle A is adjacent to angle B and angle D. Similar relations exist for all other angles.
Angles
- An angle is made by two rays starting at a common endpoint.
- These rays are called the arms of the angle.
- The common endpoint is called the vertex of the angle.
- While naming an angle, the vertex of the angle has to be in the middle.
- For example, Ray OP and Ray OQ form an angle. It can be denoted as ∠POQ.

- Ray OP and OQ are the arms or sides of the angle. O is the vertex of the angle POQ
Exterior and Interior Points to an Angle
- An angle separates its plane into three regions.
- These regions are the angle, interior of the angle and exterior of the angle.

- In the figure above, points F and R lie in the interior of ∠ABC. Points A, B and C lie on the angle ∠ABC and P, X, and T lie on the exterior of angle ∠ABC.
To know more about Angle, visit here.
Circles
- A circle is a simple closed curve which is not a polygon.
- A circle is basically formed when a point is moving at a fixed distance from a fixed point.

- This fixed point in the middle is called the centre.
- The distance moved by the point around the circle is called the circumference.
Terms Related to Circle
- The chord of a circle is a line segment joining any two points of a circle.
- A diameter is a chord passing through the centre of a circle.
- The diameter divides a circle into two equal halves called semicircles.

- A region in the interior of a circle enclosed by an arc on one side and a pair of radii on the other two sides is called a sector.
- A region in the interior of a circle enclosed by a chord and an arc is called a segment.
All About Lines
Line Segment
-
- The shortest distance between two points is called a line segment.
- Those points are called endpoints of the line segment.

Lines
- When a line segment is extended on both sides infinitely, then it is called a line. Here m is a line.
- It contains an infinite number of points on it.

Ray
- A ray is a portion of a line. It starts at one point, called its starting point, and goes endlessly in the other direction.

-
- In the ray AB, A is the starting point, and B is just a point on the path of the ray.
![]()
Intersecting and Parallel Lines
- If two lines have a common point, then they are said to be intersecting.

- Lines l and m here have a common point P, hence they are intersecting lines with P being the point of intersection.
- If two lines have no common point, then they are said to be parallel. Here AB and CD are parallel lines.

To know more about Lines, visit here.
Position in a Figure
- There are three important parts of a closed curve. In the figure below, L is in the interior of the curve, M is on the boundary while N is in the exterior of the curve.

- The interior of a curve along with the boundary is called the region of the curve.
Related Articles
| Quadrilateral | Triangles |
| Geometry | NCERT Solutions Class 6 Maths Basic Geometrical Ideas |
Frequently Asked Questions on CBSE Class 6 Maths Notes Chapter 4 Basic Geometrical Ideas
What are intersecting lines?
If two distinct lines meet or cross at a point, they are called intersecting lines.
What is a simple curve?
A curve which starts and ends at the same point without crossing itself is called a simple closed curve.
What are parallel lines?
Parallel lines can be defined as two lines in the same plane that are at equal distances from each other and never meet.

Comments