According to the CBSE Syllabus 2023-24, this chapter has been renumbered as Chapter 7.
CBSE Class 9 Science Chapter 8 Motion Notes
In Class 9 Science Chapter 8 Motion, students learn to describe the motion of objects along a straight line and express such motions through simple equations and graphs. The chapter also discusses ways of describing circular motion.

Chapter Summary Video

Understanding Motion
Reference Point and Reference Frame
- To describe the position of an object, we need a reference point or origin. An object may seem to be moving to one observer and stationary to another.
- Example: A passenger inside a bus sees the other passengers to be at rest, whereas an observer outside the bus sees the passengers to be in motion.
- In order to make observations easy, a convention or a common reference point or frame is needed. All objects must be in the same reference frame.
For more information on Motion, watch the below videos


To know more about the frame of reference, visit here.
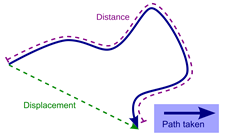
Distance and Displacement
The magnitude of the length covered by a moving object is called distance. It has no direction.
Displacement is the shortest distance between two points or the distance between the starting and final positions with respect to time. It has magnitude as well as direction.
Displacement can be zero, but distance cannot.
To know more about Distance and Displacement, visit here.
Magnitude
Magnitude is the size or extent of a physical quantity. In physics, we have scalar and vector quantities.
Scalar quantities are only expressed as magnitude. E.g.: time, distance, mass, temperature, area, volume
Vector quantities are expressed in magnitude as well as the direction of the object. E.g.: Velocity, displacement, weight, momentum, force, acceleration, etc.
Time, Average Speed and Velocity
Time and speed
Time is the duration of an event that is expressed in seconds. Most physical phenomena occur with respect to time. It is a scalar quantity.
Speed is the rate of change in distance. If a body covers a certain distance in a certain amount of time, its speed is given by
The instantaneous speed is the speed of an object at a particular moment in time.
Average speed is stated as the distance covered by the object within a period of time.
Average speed = Total distance travelled / Total time taken
The below table lists the difference between Average Speed and Instantaneous Speed.
| Average Speed | Instantaneous Speed |
| It is defined as the total distance travelled divided by the total time elapsed. | It is defined as the speed at a particular instant of time. |
| It is constant. | It is not constant. |
| Measured by calculating the speed for an entire journey. | It is measured by a speedometer. |
| Example: A car travelling with a speed of 60 kmph. Thus, the average speed of the car is 60 km an hour. | Example: A car travelling at a certain speed at an instant of time can be given by a speedometer. |
Uniform motion and Non-uniform motion
When an object covers equal distances in equal intervals of time, it is in uniform motion.
Examples of Uniform Motion
- Movement of the ceiling fan’s blades.
- Motion of Earth around the sun
- Pendulum with equivalent amplitude on either side
When an object covers unequal distances in equal intervals of time, it is said to be in non-uniform motion.
- Bouncing ball
- Running horse
- Moving train
To know more about Uniform Motion and Non-Uniform Motion, visit here.
Velocity
The Rate of change of displacement is velocity. It is a vector quantity. Here the direction of motion is specified.
Instantaneous velocity is the rate of change of position for a time interval which is very small, i.e. almost zero. In more simple words, the velocity of an object at a given instant of time is known as instantaneous velocity.
Average velocity is defined as the displacement (∆x) divided by the time intervals (∆t) in which the displacement occurs.
| Average Velocity | Instantaneous Velocity |
| Average velocity is defined as the displacement (∆x) divided by the time intervals (∆t) in which the displacement occurs. | Instantaneous velocity is the rate of change of position for a time interval which is very small, i.e. almost zero. |
| Average velocity is calculated by dividing the rate of displacement by the time elapsed. | Instantaneous velocity is calculated by dividing displacement by time at that instant. |
| If Jack took a total of 1 hour to travel 10 km from his house to school, then his average velocity will be 10 km/hr. | In Jack’s case, on his way to school, while he is sitting and waiting for the train to pass, his instantaneous velocity will be zero. Though the instantaneous velocity was zero for a small part of the journey, the average velocity will not be zero. |
For more information on Average Speed and Velocity, watch the below video

To know more about Average Speed and Average Velocity, visit here.
Acceleration
The rate of change of velocity is called acceleration. It is a vector quantity. In non-uniform motion, velocity varies with time, i.e., the change in velocity is not 0. It is denoted by “a”
Acceleration = Change in Velocity / Time
(OR)
Where t (time taken), v (final velocity) and u (initial velocity).
To know more about Acceleration, visit here.
Motion Visualised
Distance-Time Graph
- Distance-Time graphs show the change in the position of an object with respect to time.
- Linear variation = uniform motion and non-linear variations imply non-uniform motion
- The slope gives us speed

- OA implies uniform motion with constant speed as the slope is constant
- AB implies the body is at rest as the slope is zero
- B to C is a non-uniform motion
To know more about Distance-Time Graph, visit here.
Velocity-Time Graph
- Velocity-Time graphs show the change in velocity with respect to time.
- Slope gives acceleration
- The area under the curve gives displacement
- Line parallel to x-axis implies constant velocity-

OA = constant acceleration, AB = constant velocity, BC = constant retardation
To know more about Velocity-Time Graph, visit here.
Equations of Motion
The motion of an object moving at uniform acceleration can be described with the help of three equations, namely
(i) v = u + at
(ii) v2 – u2 = 2as
(iii) s = ut + (1/2)at2
where u is the initial velocity, v is the final velocity, t is the time, a is the acceleration and s is the displacement.
To know more about Equations of Motion, visit here.
Derivation of Velocity-Time Relation by Graphical Method

A body starts with some initial non-zero velocity at A and goes to B with constant acceleration a.
From the graph BD = v (final velocity) – DC = u (initial velocity)…………..(eq 1).
BD = BC – DC……………..(eq 2).
Therefore BD = at………………….(eq 3).
Substitute everything we get: at = v – u.
Rearrange to get v = u + at.
Derivation of Position-Time Relation by Graphical Method

A body starts with some initial non-zero velocity at A and goes to B with constant acceleration a
Area under the graph gives Displacement as follows:
OA = u , OC = t and BD = at
Substituting in (eq 1) we get s=
Derivation of Position-Velocity Relation by Graphical Method

A body starts with some initial non-zero velocity at A and goes to B with constant acceleration a
Displacement covered will be the area under the curve which is the trapezium OABC.
We know the area of trapezium is
OA = u and BC = v and OC = t
Substitute (eq 2) in (eq 1) and arrange to get
v2−u2=2as
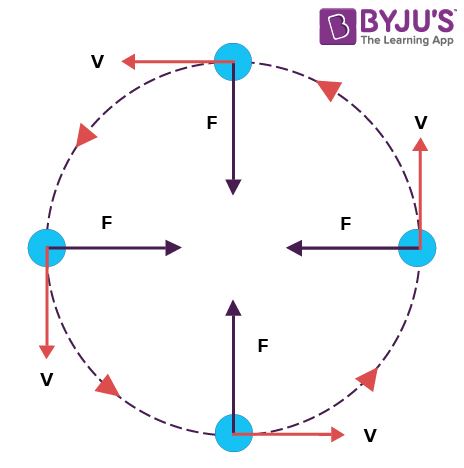
Uniform Circular Motion
Uniform Circular Motion
- If an object moves in a circular path with uniform speed, its motion is called uniform circular motion.
- Velocity changes as direction keeps changing.
- Acceleration is constant.
- The uniform circular velocity is given by the following formula: \(\begin{array}{l}v=\frac{2r}{t}\end{array} \)
Uniform Circular Motion Examples
- The motion of artificial satellites around the Earth is an example of uniform circular motion.
- The motion of electrons around its nucleus.
- The motion of blades of the windmills.
- The tip of the second hand of a watch with a circular dial shows uniform circular motion.
To know more about Uniform Circular Motion, visit here.
Frequently Asked Questions on CBSE Class 9 Science Notes Chapter 8 Motion
What is ‘motion’?
When any object moves from one point to another with respect to the observer, then this object is said to be in ‘motion’.
Is this chapter difficult?
If a student fully understands the concept of the chapter ‘motion’ and practises sums regularly, then they can score good marks in this chapter.
Are the derivations in this chapter difficult?
There are derivations in this chapter and these need to be practised constantly.

It was really helpful to me.
Its was really very helpful
Very helpful notes for me