The NCERT exercise question and answers given in PDF form will help students frame a perfect solution for the Math Exam. The solutions are aimed at helping students master the concepts by practising the problems. NCERT Solutions for Class 8 Maths Chapter 8, Comparing Quantities Exercise 8.3, are prepared by BYJU’S subject matter experts to help the students enhance their grip on the different concepts related to Compound Interest. Download NCERT Solutions for Maths Chapter 8 to strengthen the basic foundation.
NCERT Solutions for Class 8 Maths Chapter 8 – Comparing Quantities Exercise 8.3
Access Answers of Maths NCERT Class 8 Chapter 8 – Comparing Quantities Exercise 8.3 Page Number 133
Exercise 8.3 Page No: 133
1. Calculate the amount and compound interest on
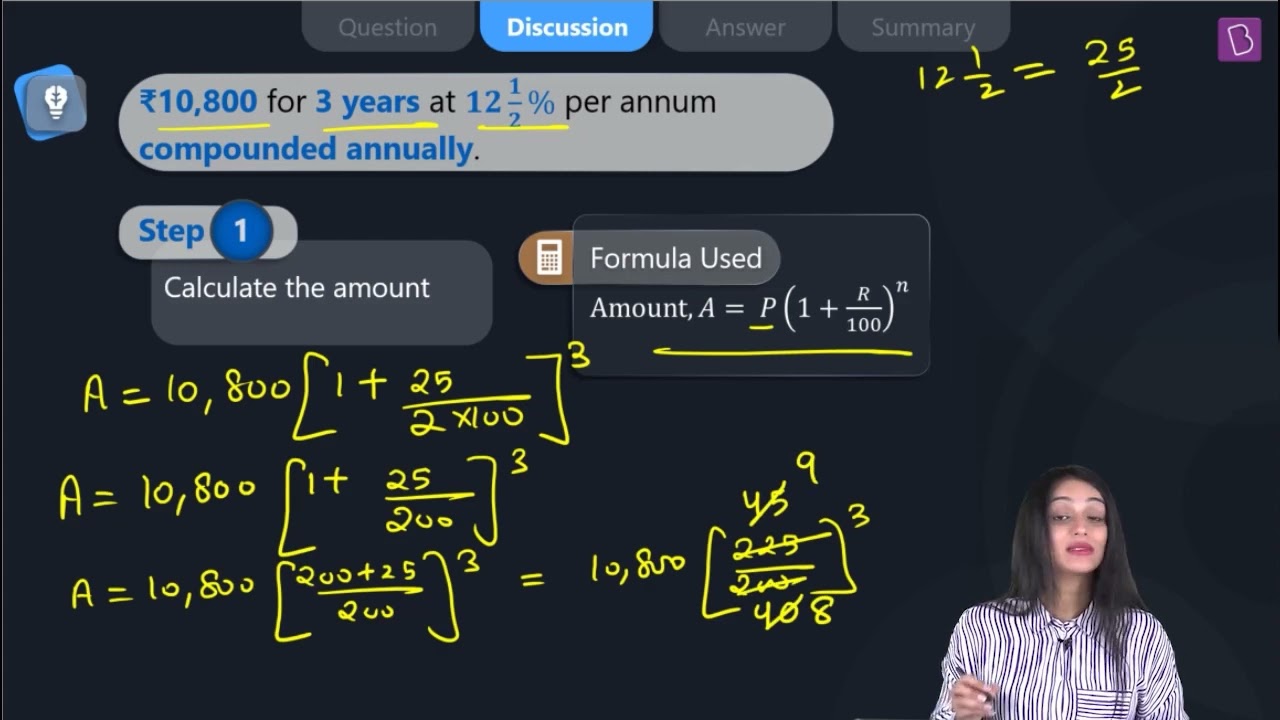
(a) ₹ 10,800 for 3 years at 12½ % per annum compounded annually.
Solution:
Principal (P) = ₹ 10,800
Rate (R) = 12½ % = 25/2 % (annual)
Number of years (n) = 3
Amount (A) = P(1 + R/100)n
= 10800(1 + 25/200)3
= 10800(225/200)3
= 15377.34375
= ₹ 15377.34 (approximately)
C.I. = A – P = ₹ (15377.34 – 10800) = ₹ 4,577.34
(b) ₹ 18000 for 2½ years at 10% per annum compounded annually.
Solution:
Principal (P) = ₹ 18,000
Rate (R) = 10% annual
Number of years (n) = 2½
The amount for 2 years and 6 months can be calculated by calculating the amount for 2 years using the compound interest formula, then calculating the simple interest for 6 months on the amount obtained at the end of 2 years.
First, the amount for 2 years has to be calculated
Amount, A = P(1 + R/100)n
= 18000(1 + 1/10)2
= 18000(11/10)2
= ₹ 21780
By taking ₹ 21780 as principal, the S.I. for the next ½ year will be calculated
S.I. = (21780 x ½ x 10)/100
= ₹ 1089
Hence, the interest for the first 2 years = ₹ (21780 – 18000) = ₹ 3780
And, interest for the next ½ year = ₹ 1089
Total C.I. = ₹ 3780 + ₹ 1089
= ₹ 4,869
Therefore,
Amount, A = P + C.I.
= ₹ 18000 + ₹ 4869
= ₹ 22,869
(c) ₹ 62500 for 1½ years at 8% per annum compounded half yearly.
Solution:
Principal (P) = ₹ 62,500
Rate = 8% per annum or 4% per half-year
Number of years = 1½
There will be 3 half-years in 1½ years
Amount, A = P(1 + R/100)n
= 62500(1 + 4/100)3
= 62500(104/100)3
= 62500(26/25)3
= ₹ 70304
C.I. = A – P = ₹ 70304 – ₹ 62500 = ₹ 7,804
(d) ₹ 8000 for 1 year at 9% per annum compound half yearly.
(You can use the year-by-year calculation using S.I. formula to verify)
Solution:
Principal (P) = ₹ 8000
Rate of interest = 9% per annum or 9/2% per half-year
Number of years = 1 year
There will be 2 half-years in 1 year
Amount, A = P(1 + R/100)n
= 8000(1 + 9/200)2
= 8000(209/200)2
= 8736.20
C.I. = A – P = ₹ 8736.20 – ₹ 8000 = ₹ 736.20
(e) ₹ 10000 for 1 year at 8% per annum compounded half yearly.
Solution:
Principal (P) = ₹ 10,000
Rate = 8% per annum or 4% per half-year
Number of years = 1 year
There are 2 half-years in 1 year
Amount, A = P(1 + R/100)n
= 10000(1 + 4/100)2
= 10000(1 + 1/25)2
= 10000(26/25)2
= ₹ 10816
C.I. = A – P = ₹ 10816 – ₹ 10000 = ₹ 816
2. Kamala borrowed ₹ 26400 from a Bank to buy a scooter at a rate of 15% p.a. compounded yearly. What amount will she pay at the end of 2 years and 4 months to clear the loan?
(Hint: Find A for 2 years with interest compounded yearly and then find S.I. on the 2nd year amount for 4/12 years.)
Solution:
Principal (P) = ₹ 26,400
Rate (R) = 15% per annum
Number of years (n) = 2 4/12
The amount for 2 years and 4 months can be calculated by first calculating the amount for 2 years using the compound interest formula, then calculating the simple interest for 4 months on the amount obtained at the end of 2 years.
First, the amount for 2 years has to be calculated
Amount, A = P(1 + R/100)n
= 26400(1 + 15/100)2
= 26400(1 + 3/20)2
= 26400(23/20)2
= ₹ 34914
By taking ₹ 34,914 as principal, the S.I. for the next 1/3 years will be calculated
S.I. = (34914 × 1/3 x 15)/100 = ₹ 1745.70
Interest for the first two years = ₹ (34914 – 26400) = ₹ 8,514
And interest for the next 1/3 year = ₹ 1,745.70
Total C.I. = ₹ (8514 + ₹ 1745.70) = ₹ 10,259.70
Amount = P + C.I. = ₹ 26400 + ₹ 10259.70 = ₹ 36,659.70
3. Fabina borrows ₹ 12,500 at 12% per annum for 3 years at simple interest, and Radha borrows the same amount for the same time period at 10% per annum, compounded annually. Who pays more interest, and by how much?
Solution:
Interest paid by Fabina = (P x R x T)/100
= (12500 x 12 x 3)/100
= 4500
Amount paid by Radha at the end of 3 years = A = P(1 + R/100)n
A = 12500(1 + 10/100)3
= 12500(110/100)3
= ₹ 16637.50
C.I. = A – P = ₹ 16637.50 – ₹ 12500 = ₹ 4,137.50
The interest paid by Fabina is ₹ 4,500 and by Radha is ₹ 4,137.50
Thus, Fabina pays more interest
₹ 4500 − ₹ 4137.50 = ₹ 362.50
Hence, Fabina will have to pay ₹ 362.50 more.
4. I borrowed ₹ 12000 from Jamshed at 6% per annum simple interest for 2 years. Had I borrowed this sum at 6% per annum compound interest, what extra amount would I have to pay?
Solution:
P = ₹ 12000
R = 6% per annum
T = 2 years
S.I. = (P x R x T)/100
= (12000 x 6 x 2)/100
= ₹ 1440
To find the compound interest, the amount (A) has to be calculated
Amount, A = P(1 + R/100)n
= 12000(1 + 6/100)2
= 12000(106/100)2
= 12000(53/50)2
= ₹ 13483.20
∴ C.I. = A − P
= ₹ 13483.20 − ₹ 12000
= ₹ 1,483.20
C.I. − S.I. = ₹ 1,483.20 − ₹ 1,440
= ₹ 43.20
Therefore, the extra amount to be paid is ₹ 43.20.
5. Vasudevan invested ₹ 60000 at an interest rate of 12% per annum compounded half yearly. What amount would he get
(i) after 6 months?
(ii) after 1 year?
Solution:
(i) P = ₹ 60,000
Rate = 12% per annum = 6% per half-year
n = 6 months = 1 half-year
Amount, A = P(1 + R/100)n
= 60000(1 + 6/100)1
= 60000(106/100)
= 60000(53/50)
= ₹ 63600
(ii) There are 2 half-years in 1 year
So, n = 2
Amount, A = P(1 + R/100)n
= 60000(1 + 6/100)2
= 60000(106/100)2
= 60000(53/50)2
= ₹ 67416
6. Arif took a loan of ₹ 80,000 from a bank. If the rate of interest is 10% per annum, find the difference in amounts he would be paying after 1½ years if the interest is
(i) Compounded annually
(ii) Compounded half yearly
Solution:
(i) P = ₹ 80,000
R = 10% per annum
n = 1½ years
The amount for 1 year and 6 months can be calculated by first calculating the amount for 1 year using the compound interest formula, then calculating the simple interest for 6 months on the amount obtained at the end of 1 year.
First, the amount for 1 year has to be calculated
Amount, A = P(1 + R/100)n
= 80000(1 + 10/100)1
= 80000 x 11/100
= ₹ 88000
By taking ₹ 88,000 as principal, the S.I. for the next ½ year will be calculated as
S.I. = (P x R x T)/100
= (88000 x 10 x ½)/100
= ₹ 4400
Interest for the first year = ₹ 88000 – ₹ 80000 = ₹ 8000
And interest for the next ½ year = ₹ 4,400
Total C.I. = ₹ 8,000 + ₹ 4,400 = ₹ 12,400
A = P + C.I.= ₹ (80000 + 12400)
= ₹ 92,400
(ii) The interest is compounded half yearly
Rate = 10% per annum = 5% per half-year
There will be three half-years in 1½ years
Amount, A = P(1 + R/100)n
= 80000(1 + 5/100)3
= 80000(105/100)3
= ₹ 92610
Thus, the difference between the amounts = ₹ 92,610 – ₹ 92,400 = ₹ 210
7. Maria invested ₹ 8,000 in a business. She would be paid interest at 5% per annum compounded annually. Find
(i) The amount credited against her name at the end of the second year
(ii) The interest for the 3rd year
Solution:
(i) P = ₹ 8,000
R = 5% per annum
n = 2 years
Amount, A = P(1 + R/100)n
= 8000(1 + 5/100)2
= 8000(105/100)2
= ₹ 8820
(ii) The interest for the next year, i.e. the third year, has to be calculated. By taking ₹ 8,820 as principal, the S.I. for the next year will be calculated.
S.I. = (P x R x T)/100
= (8820 x 5 x 1)/100
= ₹ 441
8. Find the amount and the compound interest on ₹ 10,000 for 1½ years at 10% per annum, compounded half yearly. Would this interest be more than the interest he would get if it was compounded annually?
Solution:
P = ₹ 10,000
Rate = 10% per annum = 5% per half-year
n = 1½ years
There will 3 half-years in 1½ years
Amount, A = P(1 + R/100)n
= 10000(1 + 5/100)3
= 10000(105/100)3
= ₹ 11576.25
C.I. = A − P
= ₹ 11576.25 − ₹ 10000
= ₹ 1,576.25
The amount for 1 year and 6 months can be calculated by first calculating the amount for 1 year using the compound interest formula, then calculating the simple interest for 6 months on the amount obtained at the end of 1 year.
Amount, A = P(1 + R/100)n
= 10000(1 + 10/100)1
= 10000(110/100)
= ₹ 11000
By taking ₹ 11,000 as the principal, the S.I. for the next ½ year will be calculated as
S.I. = (P x R x T)/100
= (11000 x 10 x ½)/100
= ₹ 550
So, the interest for the first year = ₹ 11000 − ₹ 10000 = ₹ 1,000
Hence, Total compound interest = ₹ 1000 + ₹ 550 = ₹ 1,550
So the difference between two interests = 1576.25 – 1550 = 26.25
Therefore, the interest would be 26.25 more when compounded half yearly than the interest when compounded annually.
9. Find the amount which Ram will get on ₹ 4,096, if he gave it for 18 months at 12½ per annum, interest being compounded half-yearly.
Solution:
P = ₹ 4,096
R = 12½ per annum = 25/2 per annum = 25/4 per half-year
n = 18 months
There will be 3 half-years in 18 months
Therefore, amount A = P(1 + R/100)n
= 4096(1 + 25/(4 x 100))3
= 4096 x (1 + 1/16)3
= 4096 x (17/16)3
= ₹ 4913
Therefore, the required amount is ₹ 4,913.
10. The population of a place increased to 54000 in 2003 at a rate of 5% per annum
(i) find the population in 2001
(ii) what would be its population in 2005?
Solution:
(i) It’s given that population in the year 2003 = 54,000
54,000 = (Population in 2001) (1 + 5/100)2
54,000 = (Population in 2001) (105/100)2
Population in 2001 = 54000 x (100/105)2
= 48979.59
Therefore, the population in the year 2001 was approximately 48,980
(ii) Population in 2005 = 54000(1 + 5/100)2
= 54000(105/100)2
= 54000(21/20)2
= 59535
Therefore, the population in the year 2005 would be 59,535.
11. In a laboratory, the count of bacteria in a certain experiment was increasing at the rate of 2.5% per hour. Find the bacteria at the end of 2 hours if the count was initially 5,06,000.
Solution:
The initial count of bacteria is given as 5,06,000
Bacteria at the end of 2 hours = 506000(1 + 2.5/100)2
= 506000(1 + 1/40)2
= 506000(41/40)2
= 531616.25
Therefore, the count of bacteria at the end of 2 hours will be 5,31,616 (approx.).
12. A scooter was bought at ₹ 42,000. Its value depreciated at the rate of 8% per annum. Find its value after one year.
Solution:
Principal = Cost price of the scooter = ₹ 42,000
Depreciation = 8% of ₹ 42,000 per year
= (P x R x T)/100
= (42000 x 8 x 1)/100
= ₹ 3360
Thus, the value after 1 year = ₹ 42000 − ₹ 3360 = ₹ 38,640.
Access other exercise solutions of Class 8 Maths Chapter 8 – Comparing Quantities
Exercise 8.1 Solutions 6 Questions (1 Long Answer Question, 5 Short Answer Questions)
Exercise 8.2 Solutions 10 Questions (4 Long Answer Questions, 6 Short Answer Questions)
NCERT Solutions for Class 8 Maths Chapter 8 – Comparing Quantities Exercise 8.3
Exercise 8.3 of NCERT Solutions for Class 8 Maths Chapter 8 – Comparing Quantities is based on
- Compound Interest
- Deducing a Formula for Compound Interest
- Rate Compounded Annually or Half Yearly (Semi-annually)
- Applications of Compound Interest Formula
Also, explore –












It’s good and helpful
This very helpful, learning and interesting app.
The Byjus app is very nice
It’s very nice and helpful
Best explained
Byjus explanation is quite good and exciting