RD Sharma Solutions Class 11 Maths Chapter 29 – Download Free PDF Updated for (2023-24)
RD Sharma Solutions for Class 11 Maths Chapter 29 – Limits are given here for students to study effectively and secure good marks in the board examination. This chapter mainly deals with problems based on limits and how it is derived. For students who find Maths a difficult subject, experts have designed the solutions in a step-wise manner to make learning fun and interesting and to help them grasp the concepts with ease. To get a clear idea about the method of solving problems, students can use RD Sharma Class 11 Maths Solutions PDF from the links given below.
Chapter 29 – Limits contains eleven exercises, and RD Sharma Solutions provide 100% accurate answers to the questions present in each exercise. The RD Sharma Solutions formulated by experts mainly contain answers with explanations in an interactive manner to help students perform well in the board exam. Now, let us have a look at the concepts discussed in this chapter.
- Informal approach to limit.
- Evaluation of left-hand and right-hand limits.
- Difference between the value of a function at a point and the limit at that point.
- The algebra of limits.
- Indeterminate forms and evaluation of limits.
- Evaluation of algebraic limits.
- Direct substitution method.
- Factorisation method.
- Rationalisation method.
- Evaluation of algebraic limits by using some standard limits.
- Method of evaluation of algebraic limits at infinity.
- Evaluation of trigonometric limits.
- Evaluation of trigonometric limits when the variable tends to zero.
- Evaluation of trigonometric limits when variables tend to a non-zero quantity.
- Evaluation of trigonometric limits by factorisation.
- Evaluation of exponential and logarithmic limits.
Download PDF 
carouselExampleControls111
Access RD Sharma Solutions for Class 11 Maths Chapter 29 – Limits
EXERCISE 29.1 PAGE NO: 29.11
1. Show that 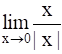 does not exist.
does not exist.
Solution:
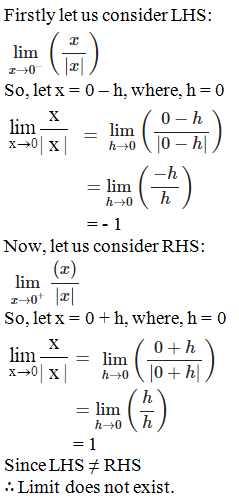
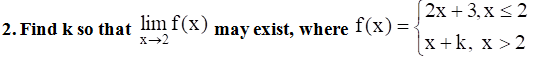
Solution:
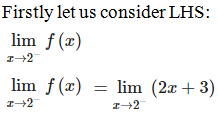
So, let x = 2 – h, where h = 0
Substituting the value of x, we get
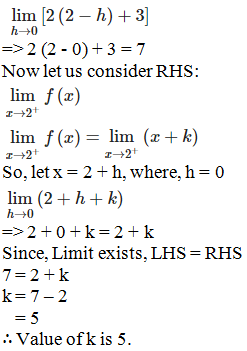
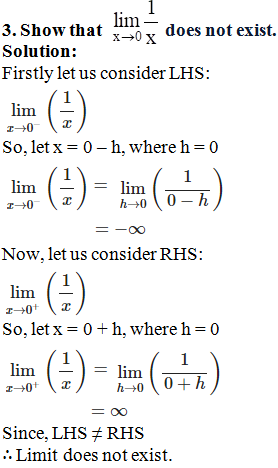

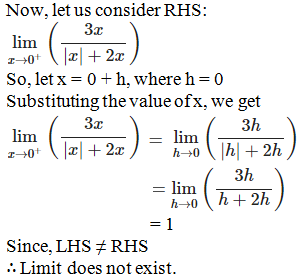
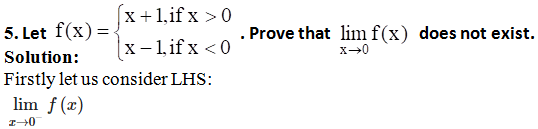
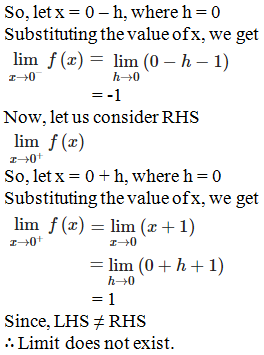
EXERCISE 29.2 PAGE NO: 29.18
Evaluate the following limits:






EXERCISE 29.3 PAGE NO: 29.23
Evaluate the following limits:




∴ The value of the given limit is ½.



By substituting the value of x, we get



EXERCISE 29.4 PAGE NO: 29.28
Evaluate the following limits:

∴ The value of the given limit is ½.

We need to find the limit of the given equation when x => 0
Now let us substitute the value of x as 0, we get an indeterminate form of 0/0.
Let us rationalise the given equation, and we get






∴ The value of the given limit is ½.
EXERCISE 29.5 PAGE NO: 29.33
Evaluate the following limits:










EXERCISE 29.6 PAGE NO: 29.38
Evaluate the following limits:


= 3 / 2





EXERCISE 29.7 PAGE NO: 29.49
Evaluate the following limits:



So,






EXERCISE 29.8 PAGE NO: 29.62
Evaluate the following limits:









EXERCISE 29.9 PAGE NO: 29.65
Evaluate the following limits:











EXERCISE 29.10 PAGE NO: 29.71
Evaluate the following limits:







EXERCISE 29.11 PAGE NO: 29.71
Evaluate the following limits:




So here,
f (x) = cos x + sin x – 1
g (x) = x
Then,



Also, access exercises of RD Sharma Solutions for Class 11 Maths Chapter 29 – Limits
Exercise 29.1 Solutions
Exercise 29.2 Solutions
Exercise 29.3 Solutions
Exercise 29.4 Solutions
Exercise 29.5 Solutions
Exercise 29.6 Solutions
Exercise 29.7 Solutions
Exercise 29.8 Solutions
Exercise 29.9 Solutions
Exercise 29.10 Solutions
Exercise 29.11 Solutions
Frequently Asked Questions on RD Sharma Solutions for Class 11 Maths Chapter 29
Q1
Are RD Sharma Solutions for Class 11 Maths Chapter 29 sufficient to score good marks in exams?
Yes, the RD Sharma Solutions are well-researched and presented by academic experts, which makes them more informative and accurate for effective exam preparation. This increases the chances of performing well in the board exam with a good score. Through regular practice, students will be able to analyse how to attempt answers as per the marks weightage of the CBSE board. This, in turn, helps them to solve complex problems with ease in a short period of time, which is crucial for the final exam.
Q2
Where can I find the accurate answers of RD Sharma Solutions for Class 11 Maths Chapter 29?
Students can find the accurate answers of RD Sharma Solutions for Class 11 Maths Chapter 29 from BYJU’S website. The expert tutors have created the solutions in an interactive manner to help students perform well in the board exam. The solutions cover all the questions from the textbook, which assist students in completing their assignments on time. Students who are not able to understand the chapter during class hours can refer to these solutions to get an overview. The solutions created are 100% accurate, as per the latest syllabus of the CBSE board.
Q3
Why is BYJU’S RD Sharma Solutions for Class 11 Maths Chapter 29 the best study material for the students?
The RD Sharma Solutions, provided at BYJU’S website, are crafted by highly experienced faculty to help students score well in the final exam. The solutions are well structured in a systematic manner, providing students with a clear overview of the important questions. Short tricks and ideas are highlighted in the solutions, which help students to answer the questions and save more time in the board exam. The exercise-wise solutions are available in PDF format with a free download option, which can be accessed by the students irrespective of time.
Q4
How do RD Sharma Solutions for Class 11 Maths Chapter 29 help students with effective exam preparation?
RD Sharma Solutions for Class 11 Maths Chapter 29 provide detailed knowledge of concepts designed by experts in a simple and lucid manner. The main objective of these solutions is to provide the best guide for students to prepare well and score good marks in exams. Those who are facing difficulty in solving textbook problems are advised to download the solutions PDFs and know the various methods, tricks and tips to solve the problems with ease. Practising these solutions on a daily basis helps students enhance their exam preparation and secure high marks in exams.
Q5
Do RD Sharma Solutions for Class 11 Maths Chapter 29 clear doubts immediately in CBSE students?
Yes, RD Sharma Solutions for Class 11 Maths Chapter 29 provide comprehensive answers which help CBSE students clear their doubts instantly and understand the concepts in-depth. Each step is explained by expert teachers in simple and understandable language as per the student’s intelligence quotient. Regular practice of these solutions helps students to clarify the doubts on their own which they come across while solving textbook problems and boost skills essential from an exam point of view.
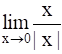 does not exist.
does not exist.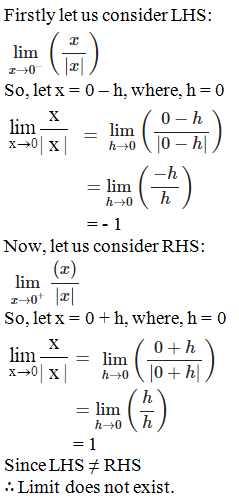
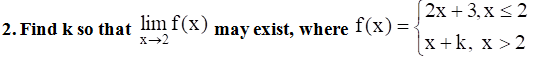
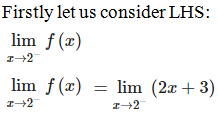
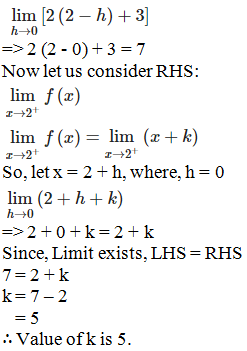
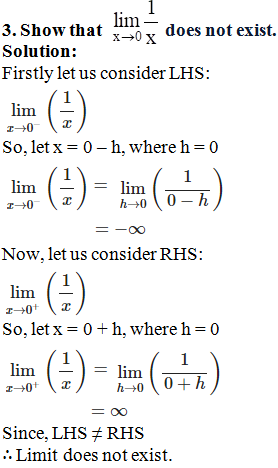

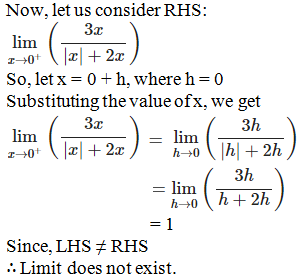
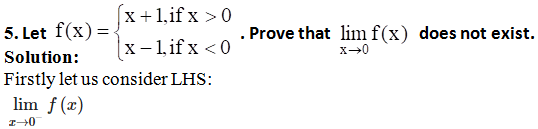
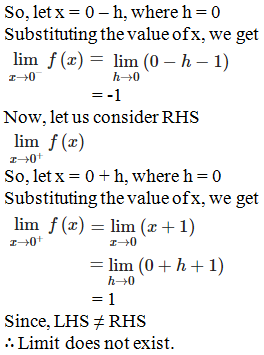
































































































































Comments