RD Sharma Solutions Class 11 Maths Chapter 6 – Free PDF Download
RD Sharma Solutions for Class 11 Maths Chapter 6 – Graphs of Trigonometric Functions are provided here. In the previous chapters, we have learnt that all trigonometric functions are periodic functions, so we shall draw their graphs on the intervals of lengths equal to their periods. In order to enhance the performance of students in the Class 11 exam, we, at BYJU’S, have formulated the RD Sharma Class 11 Solutions for Maths prescribed by the CBSE syllabus. Exercise-wise problems are solved in a step-by-step method to help students understand the concepts easily. Students are advised to download the solutions in PDF format from the links given here and practise on a regular basis to obtain good marks in their exams.
RD Sharma Solutions for Class 11 Maths Chapter 6 – Graphs of Trigonometric Functions contain three exercises. For more conceptual knowledge, students can make use of RD Sharma Solutions both online and offline mode as per their needs. Now, let us have a look at the concepts discussed in this chapter.
- Graph of the sine function
- Graph of the cosine function
- Graph of the tangent function
- Graph of the cosecant function
- Graph of the cotangent function
- Graph of the secant function
RD Sharma Solutions for Class 11 Maths Chapter 6 – Graphs of Trigonometric Functions
Also, access exercises of RD Sharma Solutions for Class 11 Maths Chapter 6 – Graphs of Trigonometric Functions
Access answers to RD Sharma Solutions for Class 11 Maths Chapter 6 – Graphs of Trigonometric Functions
EXERCISE 6.1 PAGE NO: 6.5
1. Sketch the graphs of the following functions:
(i) f (x) = 2 sin x, 0 ≤ x ≤ π
(ii) g (x) = 3 sin (x – π/4), 0 ≤ x ≤ 5π/4
(iii) h (x) = 2 sin 3x, 0 ≤ x ≤ 2π/3
(iv) ϕ (x) = 2 sin (2x – π/3), 0 ≤ x ≤ 7π/3
(v) Ψ (x) = 4 sin 3 (x – π/4), 0 ≤ x ≤ 2π
(vi) θ (x) = sin (x/2 – π/4), 0 ≤ x ≤ 4π
(vii) u (x) = sin2 x, 0 ≤ x ≤ 2π υ (x) = |sin x|, 0 ≤ x ≤ 2π
(viii) f (x) = 2 sin πx, 0 ≤ x ≤ 2
Solution:
(i) f (x) = 2 sin x, 0 ≤ x ≤ π
We know that g (x) = sin x is a periodic function with period π.
So, f (x) = 2 sin x is a periodic function with period π. So, we will draw the graph of f (x) = 2 sin x in the interval [0, π]. The values of f (x) = 2 sin x at various points in [0, π] are listed in the following table:
| x | 0(A) | π/6 (B) | π/3 (C) | π/2 (D) | 2π/3 (E) | 5π/6 (F) | Π (G) |
| f (x) = 2 sin x | 0 | 1 | √3 = 1.73 | 2 | √3 = 1.73 | 1 | 0 |
The required curve is

(ii) g (x) = 3 sin (x – π/4), 0 ≤ x ≤ 5π/4
We know that if f (x) is a periodic function with period T, then f (ax + b) is periodic with period T/|a|.
So, g (x) = 3 sin (x – π/4) is a periodic function with period π. So, we will draw the graph of g (x) = 3 sin (x – π/4) in the interval [0, 5π/4]. The values of g (x) = 3 sin (x – π/4) at various points in [0, 5π/4] are listed in the following table:
| x | 0(A) | π/4 (B) | π/2 (C) | 3π/4 (D) | π (E) | 5π/4 (F) |
| g (x) = 3 sin (x – π/4) | -3/√2 = -2.1 | 0 | 3/√2 = 2.12 | 3 | 3/√2 = 2.12 | 0 |
The required curve is

(iii) h (x) = 2 sin 3x, 0 ≤ x ≤ 2π/3
We know that g (x) = sin x is a periodic function with period 2π.
So, h (x) = 2 sin 3x is a periodic function with period 2π/3. So, we will draw the graph of h (x) = 2 sin 3x in the interval [0, 2π/3]. The values of h (x) = 2 sin 3x at various points in [0, 2π/3] are listed in the following table:
| x | 0 (A) | π/6 (B) | π/3 (C) | π/2 (D) | 2π/3 (E) |
| h (x) = 2 sin 3x | 0 | 2 | 0 | -2 | 0 |
The required curve is

(iv) ϕ (x) = 2 sin (2x – π/3), 0 ≤ x ≤ 7π/3
We know that if f(x) is a periodic function with period T, then f (ax + b) is periodic with period T/|a|.
So, ϕ (x) = 2 sin (2x – π/3) is a periodic function with period π. So, we will draw the graph of ϕ (x) = 2 sin (2x – π/3) in the interval [0, 7π/5]. The values of ϕ (x) = 2 sin (2x – π/3), at various points in [0, 7π/5] are listed in the following table:
| x | 0 (A) | π/6 (B) | 2π/3 (C) | 7π/6 (D) | 7π/5 (E) |
| ϕ (x) = 2 sin (2x – π/3) | -√3 = -1.73 | 0 | 0 | 0 | 1.98 |
The required curve is

(v) Ψ (x) = 4 sin 3 (x – π/4), 0 ≤ x ≤ 2π
We know that if f(x) is a periodic function with period T, then f (ax + b) is periodic with period T/|a|.
So, Ψ (x) = 4 sin 3 (x – π/4) is a periodic function with period 2π. So, we will draw the graph of Ψ (x) = 4 sin 3 (x – π/4) in the interval [0, 2π]. The values of Ψ (x) = 4 sin 3 (x – π/4) at various points in [0, 2π] are listed in the following table:
| x | 0 (A) | π/4 (B) | π/2 (C) | π (D) | 5π/4 (E) | 2π (F) |
| Ψ (x) = 4 sin 3 (x – π/4) | -2√2 = -2.82 | 0 | 2√2 = 2.82 | 0 | 1.98 | -2√2 = -2.82 |
The required curve is

(vi) θ (x) = sin (x/2 – π/4), 0 ≤ x ≤ 4π
We know that if f(x) is a periodic function with period T, then f (ax + b) is periodic with period T/|a|.
So, θ (x) = sin (x/2 – π/4) is a periodic function with period 4π. So, we will draw the graph of θ (x) = sin (x/2 – π/4) in the interval [0, 4π]. The values of θ (x) = sin (x/2 – π/4) at various points in [0, 4π] are listed in the following table:
| x | 0 (A) | π/2 (B) | π (C) | 2π (D) | 5π/2 (E) | 3π (F) | 4π (G) |
| θ (x) = sin (x/2 – π/4) | -1/√2 = -0.7 | 0 | 1/√2 = 0.7 | 1/√2 = 0.7 | 0 | -1/√2 = -0.7 | -1/√2 = -0.7 |
The required curve is

(vii) u (x) = sin2 x, 0 ≤ x ≤ 2π υ (x) = |sin x|, 0 ≤ x ≤ 2π
We know that g (x) = sin x is a periodic function with period π.
So, u (x) = sin2 x is a periodic function with period 2π. So, we will draw the graph of u (x) = sin2 x in the interval [0, 2π]. The values of u (x) = sin2 x at various points in [0, 2π] are listed in the following table:
| x | 0 (A) | π/2 (B) | Π (C) | 3π/2 (D) | 2π (E) |
| u (x) = sin2 x | 0 | 1 | 0 | 1 | 0 |
The required curve is

(viii) f (x) = 2 sin πx, 0 ≤ x ≤ 2
We know that g (x) = sin x is a periodic function with period 2π.
So, f (x) = 2 sin πx is a periodic function with period 2. So, we will draw the graph of f (x) = 2 sin πx in the interval [0, 2]. The values of f (x) = 2 sin πx at various points in [0, 2] are listed in the following table:
| x | 0 (A) | 1/2 (B) | 1 (C) | 3/2 (D) | 2 (E) |
| f (x) = 2 sin πx | 0 | 2 | 0 | -2 | 0 |
The required curve is

2. Sketch the graphs of the following pairs of functions on the same axes:
(i) f (x) = sin x, g (x) = sin (x + π/4)
(ii) f (x) = sin x, g (x) = sin 2x
(iii) f (x) = sin 2x, g (x) = 2 sin x
(iv) f (x) = sin x/2, g (x) = sin x
Solution:
(i) f (x) = sin x, g (x) = sin (x + π/4)
We know that the functions f (x) = sin x and g (x) = sin (x + π/4) are periodic functions with periods 2π and 7π/4.
The values of these functions are tabulated below.
Values of f (x) = sin x in [0, 2π]
| x | 0 | π/2 | π | 3π/2 | 2π |
| f (x) = sin x | 0 | 1 | 0 | -1 | 0 |
Values of g (x) = sin (x + π/4) in [0, 7π/4]
| x | 0 | π/4 | 3π/4 | 5π/4 | 7π/4 |
| g (x) = sin (x + π/4) | 1/√2 = 0.7 | 1 | 0 | -1 | 0 |
The required curve is

(ii) f (x) = sin x, g (x) = sin 2x
We know that the functions f(x) = sin x and g (x) = sin 2x are periodic functions with periods 2π and π.
The values of these functions are tabulated below.
Values of f (x) = sin x in [0, 2π]
| x | 0 | π/2 | π | 3π/2 | 2π |
| f (x) = sin x | 0 | 1 | 0 | -1 | 0 |
Values of g (x) = sin (2x) in [0, π]
| x | 0 | π/4 | π/2 | 3π/4 | π | 5π/4 | 3π/2 | 7π/4 | 2π |
| g (x) = sin (2x) | 0 | 1 | 0 | -1 | 0 | 1 | 0 | -1 | 0 |
The required curve is

(iii) f (x) = sin 2x, g (x) = 2 sin x
We know that the functions f(x) = sin 2x and g (x) = 2 sin x are periodic functions with periods π and π.
The values of these functions are tabulated below.
Values of f (x) = sin (2x) in [0, π]
| x | 0 | π/4 | π/2 | 3π/4 | π | 5π/4 | 3π/2 | 7π/4 | 2π |
| f (x) = sin (2x) | 0 | 1 | 0 | -1 | 0 | 1 | 0 | -1 | 0 |
Values of g (x) = 2 sin x in [0, π]
| x | 0 | π/2 | π | 3π/2 | 2π |
| g (x) = 2 sin x | 0 | 1 | 0 | -1 | 0 |
The required curve is

(iv) f (x) = sin x/2, g (x) = sin x
We know that the functions f(x) = sin x/2 and g (x) = sin x are periodic functions with periods π and 2π.
The values of these functions are tabulated below.
Values of f (x) = sin x/2 in [0, π]
| x | 0 | π | 2π | 3π | 4π |
| f (x) = sin x/2 | 0 | 1 | 0 | -1 | 0 |
Values of g (x) = sin (x) in [0, 2π]
| x | 0 | π/2 | π | 3π/2 | 2π | 5π/2 | 3π | 7π/2 | 4π |
| g (x) = sin (x) | 0 | 1 | 0 | -1 | 0 | 1 | 0 | -1 | 0 |
The required curve is

EXERCISE 6.2 PAGE NO: 6.8
1. Sketch the graphs of the following trigonometric functions:
(i) f (x) = cos (x – π/4)
(ii) g (x) = cos (x + π/4)
(iii) h (x) = cos2 2x
(iv) ϕ (x) = 2 cos (x – π/6)
(v) ψ (x) = cos (3x)
(vi) u (x) = cos2 x/2
(vii) f (x) = cos πx
(viii) g (x) = cos 2π x
Solution:
(i) f (x) = cos (x – π/4)
We know that g (x) = cos x is a periodic function with period 2π.
So, f (x) = cos (x – π/4) is a periodic function with period π. So, we will draw the graph of f (x) = cos (x – π/4) in the interval [0, π]. The values of f (x) = cos (x – π/4) at various points in [0, π] are listed in the following table:
| x | 0 (A) | π/4 (B) | π/2 (C) | 3π/4 (D) | π (E) | 5π/4 (F) | 3π/2 (G) | 7π/4 (H) |
| f (x) = cos (x – π/4) | 1/√2 = 0.7 | 1 | 1/√2 = 0.7 | 0 | -1/√2 = -0.7 | -1 | -1/√2 = -0.7 | 0 |
The required curve is

(ii) g (x) = cos (x + π/4)
We know that f (x) = cos x is a periodic function with period 2π.
So, g (x) = cos (x + π/4) is a periodic function with period π. So, we will draw the graph of g (x) = cos (x + π/4) in the interval [0, π]. The values of g (x) = cos (x + π/4) at various points in [0, π] are listed in the following table:
| x | 0 (A) | π/4 (B) | π/2 (C) | 3π/4 (D) | π (E) | 5π/4 (F) | 3π/2 (G) | 7π/4 (H) |
| g (x) = cos (x + π/4) | 1/√2 = 0.7 | 0 | -1/√2 = -0.7 | -1 | -1/√2 = -0.7 | 0 | 1/√2 = 0.7 | 1 |
The required curve is

(iii) h (x) = cos2 2x
We know that f (x) = cos x is a periodic function with period 2π.
So, h (x) = cos2 2x is a periodic function with period π. So, we will draw the graph of h (x) = cos2 2x in the interval [0, π]. The values of h (x) = cos2 2x at various points in [0, π] are listed in the following table:
| x | 0 (A) | π/4 (B) | π/2 (C) | 3π/4 (D) | π (E) | 5π/4 (F) | 3π/2 (G) |
| h (x) = cos2 2x | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
The required curve is

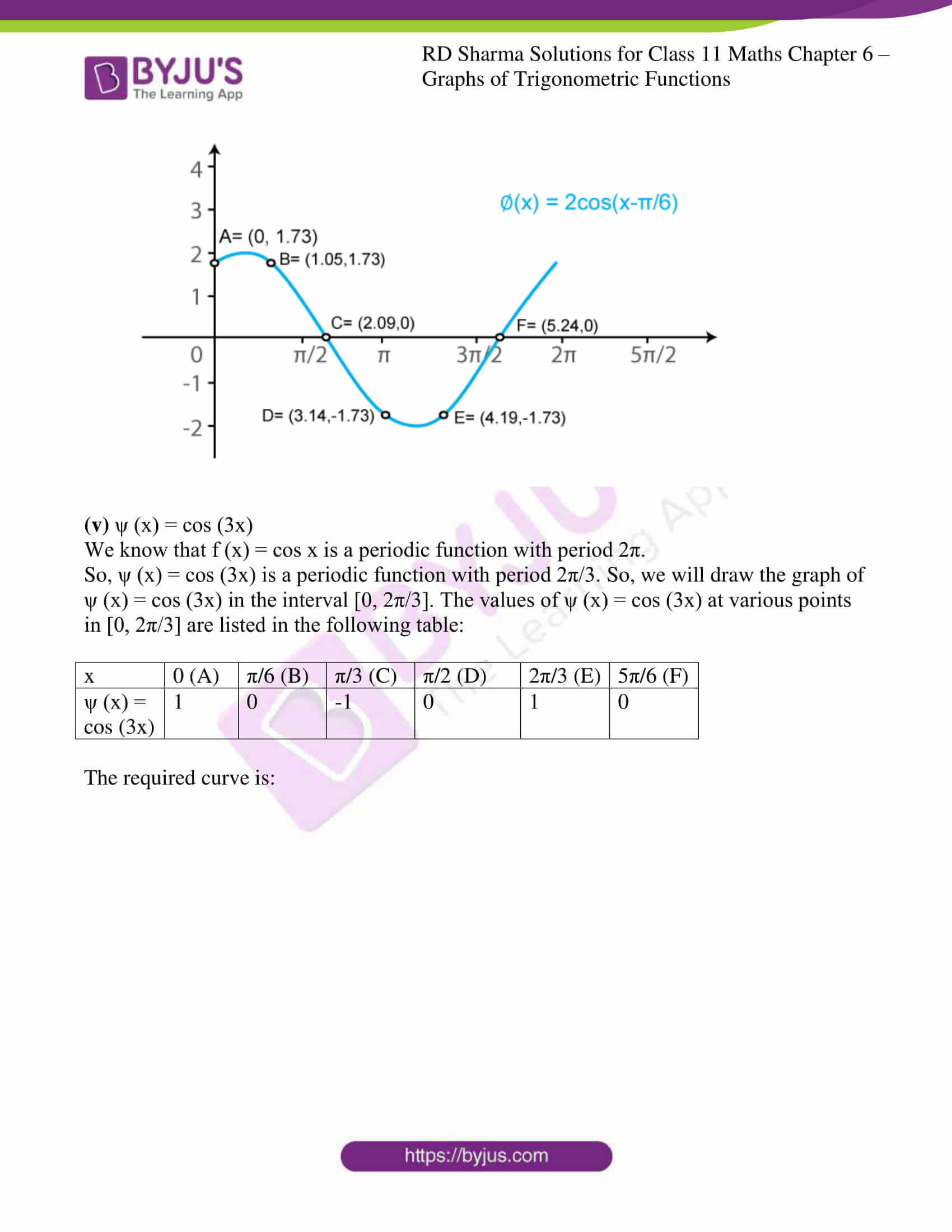
(iv) ϕ (x) = 2 cos (x – π/6)
We know that f (x) = cos x is a periodic function with period 2π.
So, ϕ (x) = 2cos (x – π/6) is a periodic function with period π. So, we will draw the graph of ϕ (x) = 2cos (x – π/6) in the interval [0, π]. The values of ϕ (x) = 2cos (x – π/6) at various points in [0, π] are listed in the following table:
| x | 0 (A) | π/3 (B) | 2π/3 (C) | π (D) | 4π/3 (E) | 5π/3 (F) |
| ϕ (x) = 2 cos (x – π/6) | √3 = 1.73 | √3 = 1.73 | 0 | -√3 = -1.73 | -√3 = -1.73 | 0 |
The required curve is

(v) ψ (x) = cos (3x)
We know that f (x) = cos x is a periodic function with period 2π.
So, ψ (x) = cos (3x) is a periodic function with period 2π/3. So, we will draw the graph of ψ (x) = cos (3x) in the interval [0, 2π/3]. The values of ψ (x) = cos (3x) at various points in [0, 2π/3] are listed in the following table:
| x | 0 (A) | π/6 (B) | π/3 (C) | π/2 (D) | 2π/3 (E) | 5π/6 (F) |
| ψ (x) = cos (3x) | 1 | 0 | -1 | 0 | 1 | 0 |
The required curve is

(vi) u (x) = cos2 x/2
We know that f (x) = cos x is a periodic function with period 2π.
So, u (x) = cos2 (x/2) is a periodic function with period π. So, we will draw the graph of u (x) = cos2 (x/2) in the interval [0, π]. The values of u (x) = cos2 (x/2) at various points in [0, π] are listed in the following table:
| x | 0 (A) | π (B) | 2π (C) | 3π (D) |
| u (x) = cos2 x/2 | 1 | 0 | 1 | 0 |
The required curve is

(vii) f (x) = cos πx
We know that g (x) = cos x is a periodic function with period 2π.
So, f (x) = cos (πx) is a periodic function with period 2. So, we will draw the graph of f (x) = cos (πx) in the interval [0, 2]. The values of f (x) = cos (πx) at various points in [0, 2] are listed in the following table:
| x | 0 (A) | 1/2 (B) | 1 (C) | 3/2 (D) | 2 (E) | 5/2 (F) |
| f (x) = cos πx | 1 | 0 | -1 | 0 | 1 | 0 |
The required curve is

(viii) g (x) = cos 2π x
We know that f (x) = cos x is a periodic function with period 2π.
So, g (x) = cos (2πx) is a periodic function with period 1. So, we will draw the graph of g (x) = cos (2πx) in the interval [0, 1]. The values of g (x) = cos (2πx) at various points in [0, 1] are listed in the following table:
| x | 0 (A) | 1/4 (B) | 1/2 (C) | 3/4 (D) | 1 (E) | 5/4 (F) | 3/2 (G) | 7/4 (H) | 2 |
| g (x) = cos 2π x | 1 | 0 | -1 | 0 | 1 | 0 | -1 | 0 | 1 |
The required curve is

2. Sketch the graphs of the following curves on the same scale and the same axes:
(i) y = cos x and y = cos (x – π/4)
(ii) y = cos 2x and y = cos (x – π/4)
(iii) y = cos x and y = cos x/2
(iv) y = cos2 x and y = cos x
Solution:
(i) y = cos x and y = cos (x – π/4)
We know that the functions y = cos x and y = cos (x – π/4) are periodic functions with periods π and π.
The values of these functions are tabulated below:
| x | 0 | π/4 | π/2 | 3π/4 | π | 5π/4 | 3π/2 | 7π/4 |
| y = cos x | 1 | 1/√2 = 0.7 | 0 | -1/√2 = -0.7 | -1 | -1/√2 = -0.7 | 0 | 1 |
| y = cos (x – π/4) | 1/√2 = 0.7 | 1 | 1/√2 = 0.7 | 0 | -1/√2 = -0.7 | -1 | -1/√2 = -0.7 | 0 |
The required curve is

(ii) y = cos 2x and y = cos 2(x – π/4)
We know that the functions y = cos 2x and y = cos 2(x – π/4) are periodic functions with periods π and π.
The values of these functions are tabulated below:
| x | 0 | π/4 | π/2 | 3π/4 | π | 5π/4 | 3π/2 | 7π/4 |
| y = cos x | 1 | 0 | -1 | 0 | 1 | 0 | -1 | 0 |
| y = cos 2 (x – π/4) | 0 | 1 | 0 | -1 | 0 | 1 | 0 | -1 |
The required curve is

(iii) y = cos x and y = cos x/2
We know that the functions y = cos x and y = cos (x/2) are periodic functions with periods π and π.
The values of these functions are tabulated below:
| x | 0 | π/2 | π | 3π/2 | 2π |
| y = cos x | 1 | 0 | -1 | 0 | 1 |
| y = cos x/2 | 1 | 1/√2 = 0.7 | 0 | -1/√2 = -0.7 | -1 |
The required curve is

(iv) y = cos2 x and y = cos x
We know that the functions y = cos2 x and y = cos x are periodic functions with period 2π.
The values of these functions are tabulated below:
| x | 0 | π/2 | π | 3π/2 | 2π |
| y = cos2 x | 1 | 0 | 1 | 0 | 1 |
| y = cos x | 1 | 0 | -1 | 0 | 1 |
The required curve is

EXERCISE 6.3 PAGE NO: 6.13
Sketch the graphs of the following functions:
1. f (x) = 2 cosec πx
Solution:
We know that f (x) = cosec x is a periodic function with period 2π.
So, f (x) = 2 cosec (πx) is a periodic function with period 2. So, we will draw the graph of f (x) = 2 cosec (πx) in the interval [0, 2]. The values of f (x) = 2 cosec (πx) at various points in [0, 2] are listed in the following table:
| x | 0 (A) | 1/2 (B) | 1 (C) | -1 (D) | 3/2 (E) | -2 (F) | 2 (G) | 5/2 (H) |
| f (x) = 2 cosec (πx) | ∞ | 2 | ∞ | -∞ | -2 | -∞ | ∞ | 2 |
The required curve is

2. f (x) = 3 sec x
Solution:
We know that f (x) = sec x is a periodic function with period π.
So, f (x) = 3 sec (x) is a periodic function with period π. So, we will draw the graph of f (x) = 3 sec (x) in the interval [0, π]. The values of f (x) = 3 sec (x) at various points in [0, π] are listed in the following table:
| x | 0 (A) | π/2 (B) | -π/2 (C) | π (D) | -3π/2 (E) | 3π/2 (F) | 2π (G) | 5π/2 (H) |
| f (x) = sec x | 3 | ∞ | -∞ | -3 | -∞ | ∞ | 3 | ∞ |
The required curve is

3. f (x) = cot 2x
Solution:
We know that f (x) = cot x is a periodic function with period π.
So, f (x) = cot (2x) is a periodic function with period π. So, we will draw the graph of f (x) = cot (2x) in the interval [0, π]. The values of f (x) = cot (2x) at various points in [0, π] are listed in the following table:
| x | 0 (A) | π/4 (B) | -π/2 (C) | π/2 (D) | 3π/4 (E) | -π (F) |
| f (x) = cot x | →∞ | 0 | -∞ | →∞ | 0 | -∞ |
The required curve is

4. f (x) = 2 sec πx
Solution:
We know that f (x) = sec x is a periodic function with period π.
So, f (x) = 2 sec (πx) is a periodic function with period 1. So, we will draw the graph of f (x) = 2 sec (πx) in the interval [0, 1]. The values of f (x) = 2 sec (πx) at various points in [0, 1] are listed in the following table:
| x | 0 | 1/2 | -1/2 | 1 | -3/2 | 3/2 | 2 |
| f (x) = 2 sec (πx) | 2 | ∞ | →-∞ | -2 | -∞ | ∞ | 2 |
The required curve is

5. f (x) = tan2 x
Solution:
We know that f (x) = tan x is a periodic function with period π.
So, f (x) = tan2 (x) is a periodic function with period π. So, we will draw the graph of f (x) = tan2 (x) in the interval [0, π]. The values of f (x) = tan2 (x) at various points in [0, π] are listed in the following table:
| x | 0 (A) | π/2 (B) | π/2 (C) | π (D) | 3π/2 (E) | 3π/2 (F) | 2 π |
| f (x) = tan2 (x) | 0 | ∞ | →∞ | 0 | ∞ | →∞ | 0 |
The required curve is

Frequently Asked Questions on RD Sharma Solutions for Class 11 Maths Chapter 6
List out the important concepts discussed in RD Sharma Solutions for Class 11 Maths Chapter 6.
The important concepts discussed in RD Sharma Solutions for Class 11 Maths Chapter 6 are listed below.
- Graph of the sine function
- Graph of the cosine function
- Graph of the tangent function
- Graph of the cosecant function
- Graph of the cotangent function
- Graph of the secant function
























Comments