In Exercise 25.1 of Chapter 25, we will discuss concepts related to pie diagrams or pie charts and the construction of pie diagrams. Students having any difficulties in solving problems can access RD Sharma Class 8 Solutions. Our experts have solved the problems in a simple and easily understandable manner, which any student can understand and, thereby, score well in their exams. To access the RD Sharma Solutions Class 8 Maths Chapter 25, students can download the PDFs from the links given below.
RD Sharma Solutions for Class 8 Maths Exercise 25.1 Chapter 25 Data Handling – III (Pictorial Representation of Data as Pie Charts or Circle Graphs)
Access Answers to RD Sharma Maths Solutions for Class 8 Chapter 25 Exercise 25.1 Data Handling – III (Pictorial Representation of Data as Pie Charts or Circle Graphs)
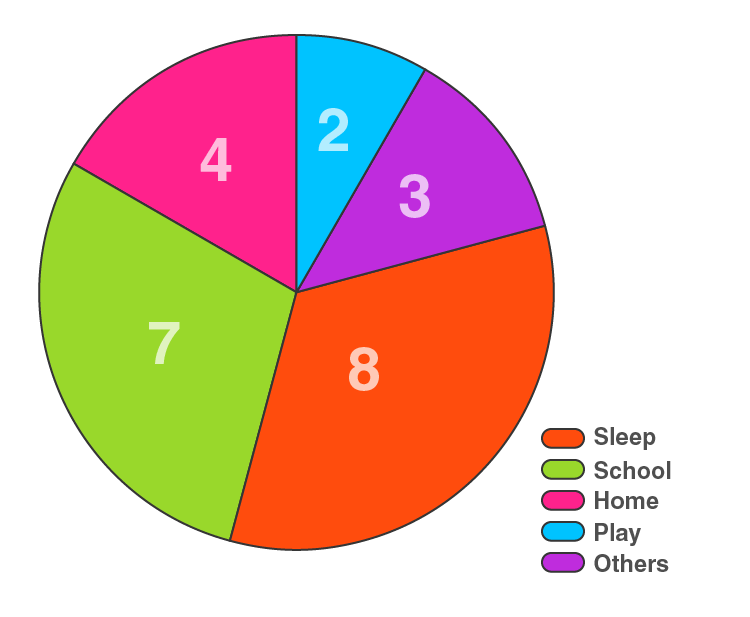
1. The number of hours spent by a schoolboy on different activities in a working day is given below:
| Activities | Sleep | School | Home | Play | Others | Total |
| Number of Hours | 8 | 7 | 4 | 2 | 3 | 24 |
Present the information in the form of a pie chart.
Solution:
Here, the total number of hours = 24
So,
The central angle = (component value/24) × 360°
The central angle for each activity will be calculated as follows:
| Activity | Number of Hours | Central Angle |
| Sleep | 8 | 8/24 × 360° = 120o |
| School | 7 | 7/24 × 360° = 105o |
| Home | 4 | 4/24 × 360° = 60o |
| Play | 2 | 2/24 × 360° = 30o |
| Others | 3 | 3/24 × 360° = 45o |
Now, the pie chart can be constructed by using the given data.
Steps to construct:
Step 1: Draw the circle of an appropriate radius.
Step 2: Draw a vertical radius anywhere inside the circle.
Step 3: Choose the largest central angle. Here, it is 120o. Construct a sector of central angle 120o whose one radius coincides with the radius drawn in step 2, and the other radius is in a clockwise direction to the vertical radius.
Step 4: Construct other sectors representing other values in a clockwise direction in descending order of magnitudes of their central angles.
Step 5: Shade the sectors so obtained by different colours and label them as shown in the below figure.
2. Employees of a company have been categorised according to their religions as given below:
| Religious | Hindu | Muslim | Sikh | Christian | Others | Total |
| Number of Workers | 420 | 300 | 225 | 105 | 30 | 1080 |
Draw a pie chart to represent the above information.
Solution:
Here, the total number of workers = 1080
So,
The central angle = (component value/1080) × 360°
The central angle for each activity will be calculated as follows:
| Religious | Number of Workers | Central Angle |
| Hindu | 420 | 420/1080 × 360° = 144 |
| Muslim | 300 | 300/1080 × 360° = 100 |
| Sikh | 225 | 225/1080 × 360° = 75 |
| Christian | 105 | 105/1080 × 360° = 35 |
| Others | 30 | 30/1080 × 360° = 10 |
Now, the pie chart can be constructed by using the given data.
Steps to construct:
Step 1: Draw the circle of an appropriate radius.
Step 2: Draw a vertical radius anywhere inside the circle.
Step 3: Choose the largest central angle. Construct a sector of a central angle, whose one radius coincides with the radius drawn in step 2, and the other radius is in a clockwise direction to the vertical radius.
Step 4: Construct other sectors representing other values in a clockwise direction in descending order of magnitudes of their central angles.
Step 5: Shade the sectors so obtained by different colours and label them as shown in the below figure.

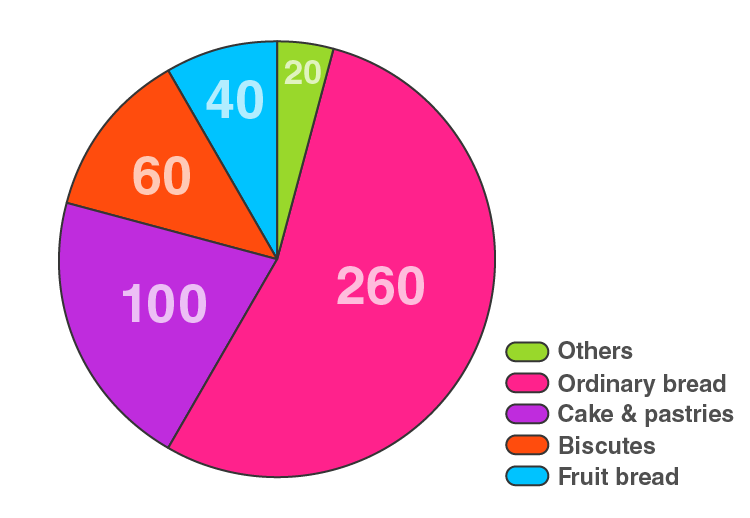
3. In one day, the sales (in rupees) of different items of a baker’s shop are given below:
| Items | Ordinary Bread | Fruit Bread | Cakes and Pastries | Biscuits | Others | Total |
| Sales (in Rs) | 260 | 40 | 100 | 60 | 20 | 480 |
Draw a pie chart to represent the above information.
Solution:
Here, total sales = 480
So,
The central angle = (component value/480) × 360°
The central angle for each activity will be calculated as follows:
| Items | Sales (in Rs) | Central Angle |
| Ordinary bread | 260 | 260/480 × 360° = 195 |
| Fruit bread | 40 | 40/480 × 360° = 30 |
| Cakes and pastries | 100 | 100/480 × 360° = 75 |
| Biscuits | 60 | 60/480 × 360° = 45 |
| Others | 20 | 20/480 × 360° = 15 |
Now, the pie chart can be constructed by using the given data.
Steps to construct:
Step 1: Draw the circle of an appropriate radius.
Step 2: Draw a vertical radius anywhere inside the circle.
Step 3: Choose the largest central angle. Construct a sector of a central angle, whose one radius coincides with the radius drawn in step 2, and the other radius is in a clockwise direction to the vertical radius.
Step 4: Construct other sectors representing other values in a clockwise direction in descending order of magnitudes of their central angles.
Step 5: Shade the sectors so obtained by different colours and label them as shown in the below figure.
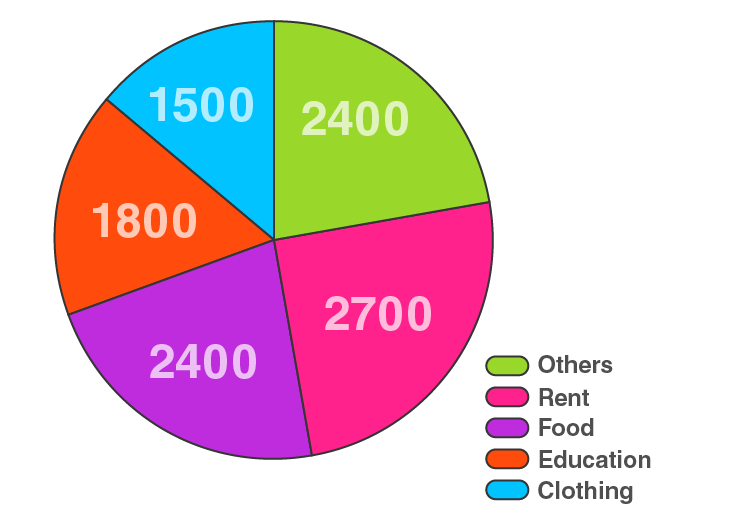
4. The following data shows the expenditure of a person on different items during a month. Represent the data in a pie chart.
| Items of Expenditure | Rent | Education | Food | Clothing | Others |
| Amount (in Rs) | 2700 | 1800 | 2400 | 1500 | 2400 |
Solution:
Here, total amount = Rs. 10800
So,
The central angle = (component value/10800) × 360°
The central angle for each activity will be calculated as follows:
| Items of Expenditure | Amount (in Rs) | Central Angle |
| Rent | 2700 | 2700/10800 × 360° = 90 |
| Education | 1800 | 1800/10800 × 360° = 60 |
| Food | 2400 | 2400/10800 × 360° = 80 |
| Clothing | 1500 | 1500/10800 × 360° = 50 |
| Others | 2400 | 2400/10800 × 360° = 80 |
Now, the pie chart can be constructed by using the given data.
Steps to construct:
Step 1: Draw the circle of an appropriate radius.
Step 2: Draw a vertical radius anywhere inside the circle.
Step 3: Choose the largest central angle. Construct a sector of a central angle, whose one radius coincides with the radius drawn in step 2, and the other radius is in a clockwise direction to the vertical radius.
Step 4: Construct other sectors representing other values in a clockwise direction in descending order of magnitudes of their central angles.
Step 5: Shade the sectors so obtained by different colours and label them as shown in the below figure.
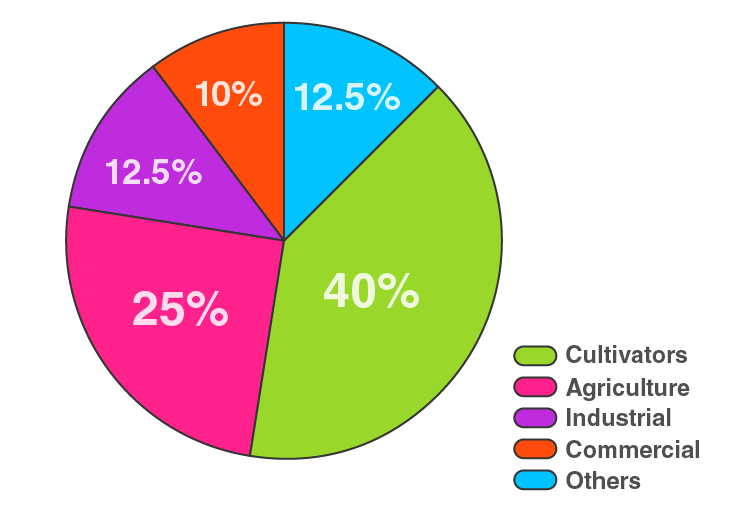
5. The percentages of various categories of workers in a state are given in the following table.
| Categories | Cultivators | Agricultural Labourers | Industrial Workers | Commercial Workers | Others |
| % of Workers | 40 | 25 | 12.5 | 10 | 12.5 |
Present the information in the form of a pie chart.
Solution:
Here, total % of workers = 100%
So,
The central angle = (component value/100) × 360°
The central angle for each activity will be calculated as follows:
| Categories | % of Workers | Central Angle |
| Cultivators | 40 | 400/100 × 360° = 144 |
| Agricultural Labourers | 25 | 25/100 × 360° = 90 |
| Industrial Workers | 12.5 | 12.5/100 × 360° = 45 |
| Commercial Workers | 10 | 10/100 × 360° = 36 |
| Others | 12.5 | 12.5/100 × 360° = 45 |
Now, the pie chart can be constructed by using the given data.
Steps to construct:
Step 1: Draw the circle of an appropriate radius.
Step 2: Draw a vertical radius anywhere inside the circle.
Step 3: Choose the largest central angle. Construct a sector of a central angle, whose one radius coincides with the radius drawn in step 2, and the other radius is in a clockwise direction to the vertical radius.
Step 4: Construct other sectors representing other values in a clockwise direction in descending order of magnitudes of their central angles.
Step 5: Shade the sectors so obtained by different colours and label them as shown in the below figure.
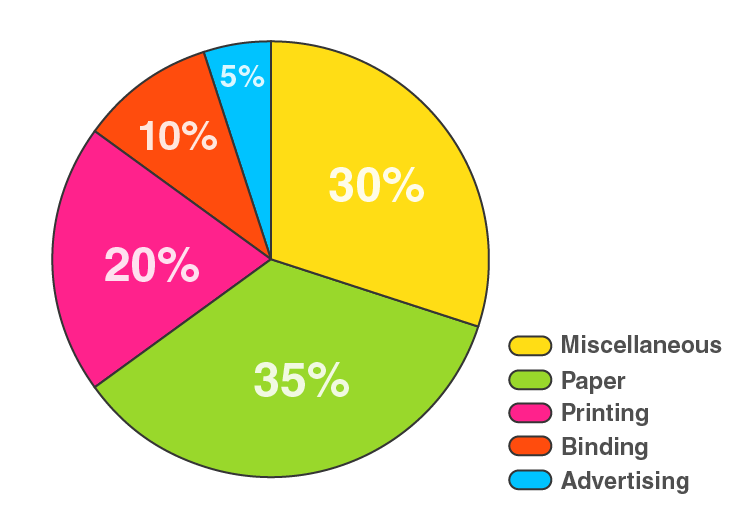
6. The following table shows the expenditure incurred by a publisher in publishing a book:
| Items | Papers | Printing | Binding | Advertising | Miscellaneous |
| Expenditure (in %) | 35% | 20% | 10% | 5% | 30% |
Present the above data in the form of pie chart.
Solution:
Here, total Expenditure (in %) = 100%
So,
The central angle = (component value/100) × 360°
The central angle for each activity will be calculated as follows:
| Items | Expenditure (in %) | Central Angle |
| Papers | 35% | 35/100 × 360° = 126 |
| Printing | 20% | 20/100 × 360° = 72 |
| Binding | 10% | 10/100 × 360° = 36 |
| Advertising | 5% | 5/100 × 360° = 18 |
| Miscellaneous | 30% | 30/100 × 360° = 108 |
Now, the pie chart can be constructed by using the given data.
Steps to construct:
Step 1: Draw the circle of an appropriate radius.
Step 2: Draw a vertical radius anywhere inside the circle.
Step 3: Choose the largest central angle. Construct a sector of a central angle, whose one radius coincides with the radius drawn in step 2, and the other radius is in a clockwise direction to the vertical radius.
Step 4: Construct other sectors representing other values in a clockwise direction in descending order of magnitudes of their central angles.
Step 5: Shade the sectors so obtained by different colours and label them as shown in the below figure.
7. The percentage of the different products of a village in a particular district is given below. Draw a pie chart representing this information.
| Items | Wheat | Pulses | Jwar | Groundnuts | Vegetables | Total |
| % | 125/3 | 125/6 | 25/2 | 50/3 | 25/3 | 100 |
Solution:
Here, total % = 100%
So,
The central angle = (component value/100) × 360°
The central angle for each activity will be calculated as follows:
| Items | % | Central Angle |
| Wheat | 125/3 | (125/3)/100 × 360° = 150 |
| Pulses | 125/6 | (125/6)/100 × 360° = 75 |
| Jwar | 25/2 | (25/2)/100 × 360° = 45 |
| Groundnuts | 50/3 | (50/3)/100 × 360° = 60 |
| Vegetables | 25/3 | (25/3)/100 × 360° = 30 |
Now, the pie chart can be constructed by using the given data.
Steps to construct:
Step 1: Draw the circle of an appropriate radius.
Step 2: Draw a vertical radius anywhere inside the circle.
Step 3: Choose the largest central angle. Construct a sector of a central angle, whose one radius coincides with the radius drawn in step 2, and the other radius is in a clockwise direction to the vertical radius.
Step 4: Construct other sectors representing other values in a clockwise direction in descending order of magnitudes of their central angles.
Step 5: Shade the sectors so obtained by different colours and label them as shown in the below figure.

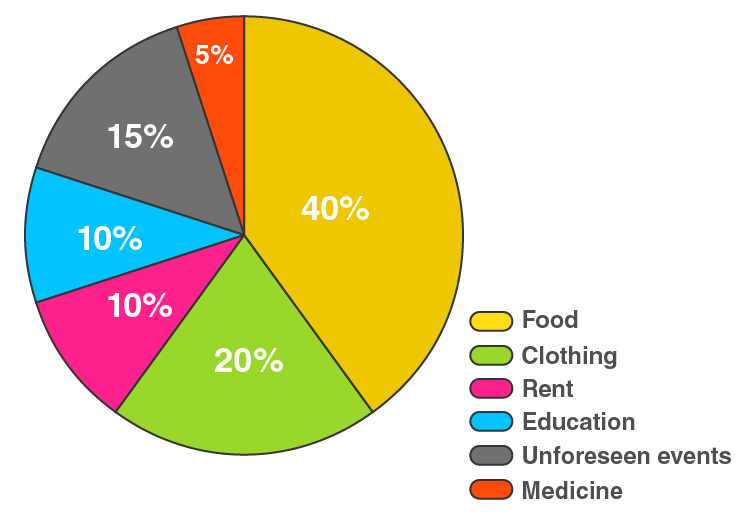
8. Draw a pie diagram for the following data of expenditure pattern in a family:
| Items | Food | Clothing | Rent | Education | Unforeseen events | Medicine |
| Expenditure (in %) | 40% | 20% | 10% | 10% | 15% | 5% |
Solution:
Here, total % = 100%
So,
The central angle = (component value/100) × 360°
The central angle for each activity will be calculated as follows:
| Items | Expenditure (in %) | Central Angle |
| Food | 40% | 40/100 × 360° = 144 |
| Clothing | 20% | 20/100 × 360° = 72 |
| Rent | 10% | 10/100 × 360° = 36 |
| Education | 10% | 10/100 × 360° = 36 |
| Unforeseen events | 15% | 15/100 × 360° = 54 |
| Medicines | 5% | 5/100 × 360° = 18 |
Now, the pie chart can be constructed by using the given data.
Steps to construct:
Step 1: Draw the circle of an appropriate radius.
Step 2: Draw a vertical radius anywhere inside the circle.
Step 3: Choose the largest central angle. Construct a sector of a central angle, whose one radius coincides with the radius drawn in step 2, and the other radius is in a clockwise direction to the vertical radius.
Step 4: Construct other sectors representing other values in a clockwise direction in descending order of magnitudes of their central angles.
Step 5: Shade the sectors so obtained by different colours and label them as shown in the below figure.
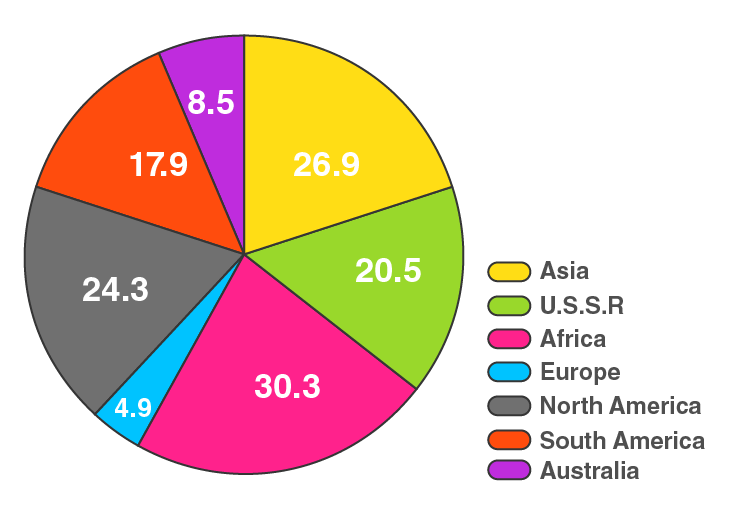
9. Draw a pie diagram of the areas of continents of the world given in the following table:
| Continents | Asia | U.S.S.R | Africa | Europe | North America | South America | Australia |
| Area (in million sq. km) | 26.9 | 20.5 | 30.3 | 4.9 | 24.3 | 17.9 | 8.5 |
Solution:
Here, the total area = 133.3 million sq. km
So,
The central angle = (component value/133.3) × 360°
The central angle for each activity will be calculated as follows:
| Continents | Area (in million sq. km) | Central Angle |
| Asia | 26.9 | 26.9/133.3 × 360° = 72.6 |
| U.S.S.R | 20.5 | 20.5/133.3 × 360° = 55.4 |
| Africa | 30.3 | 30.3/133.3 × 360° = 81.8 |
| Europe | 4.9 | 4.9/133.3 × 360° = 13.2 |
| North America | 24.3 | 24.3/133.3 × 360° = 65.6 |
| South America | 17.9 | 17.9/133.3 × 360° = 48.3 |
| Australia | 8.5 | 8.5/133.3 × 360° = 23 |
Now, the pie chart can be constructed by using the given data.
Steps to construct:
Step 1: Draw the circle of an appropriate radius.
Step 2: Draw a vertical radius anywhere inside the circle.
Step 3: Choose the largest central angle. Construct a sector of a central angle, whose one radius coincides with the radius drawn in step 2, and the other radius is in a clockwise direction to the vertical radius.
Step 4: Construct other sectors representing other values in a clockwise direction in descending order of magnitudes of their central angles.
Step 5: Shade the sectors so obtained by different colours and label them as shown in the below figure.
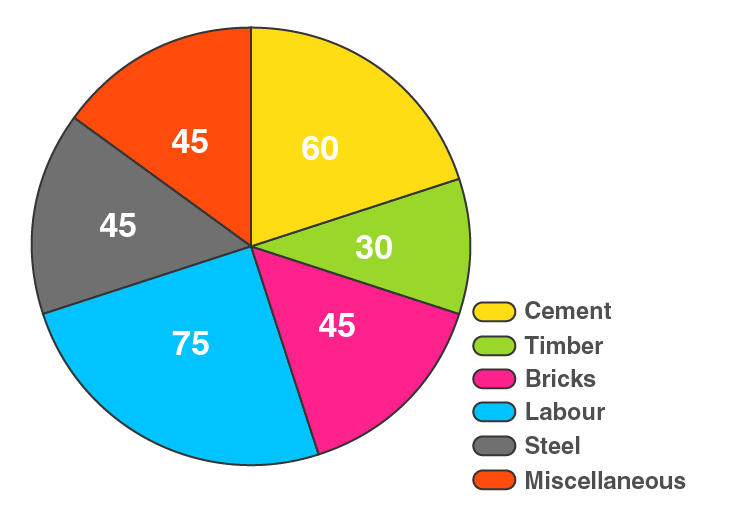
10. The following data gives the amount spent on the construction of a house. Draw a pie diagram.
| Items | Cement | Timber | Bricks | Labour | steel | Miscellaneous |
| Expenditure (in thousand Rs) | 60 | 30 | 45 | 75 | 45 | 45 |
Solution:
Here, total Expenditure = 300 thousand rupees
So,
The central angle = (component value/300) × 360°
The central angle for each activity will be calculated as follows:
| Items | Expenditure (in thousand Rs) | Central Angle |
| Cement | 60 | 60/300 × 360° = 72 |
| Timber | 30 | 30/300 × 360° = 36 |
| Bricks | 45 | 45/300 × 360° = 54 |
| Labour | 75 | 75/300 × 360° = 90 |
| Steel | 45 | 45/300 × 360° = 54 |
| Miscellaneous | 45 | 45/300 × 360° = 54 |
Now, the pie chart can be constructed by using the given data.
Steps to construct:
Step 1: Draw the circle of an appropriate radius.
Step 2: Draw a vertical radius anywhere inside the circle.
Step 3: Choose the largest central angle. Construct a sector of a central angle, whose one radius coincides with the radius drawn in step 2, and the other radius is in a clockwise direction to the vertical radius.
Step 4: Construct other sectors representing other values in a clockwise direction in descending order of magnitudes of their central angles.
Step 5: Shade the sectors so obtained by different colours and label them as shown in the below figure.
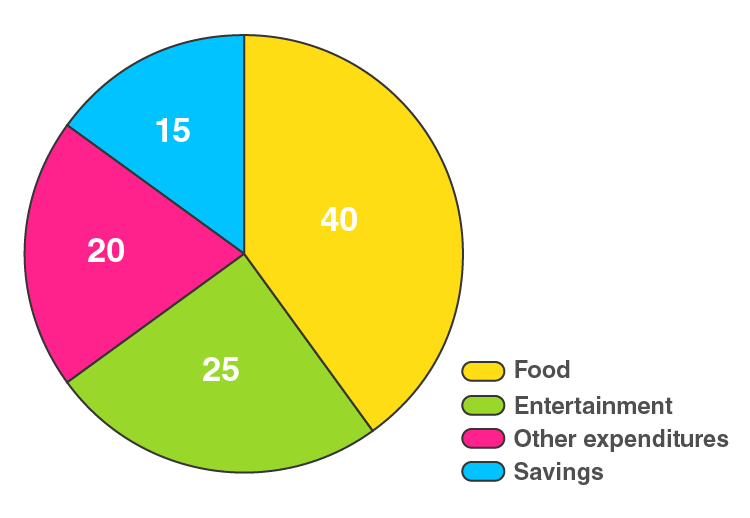
11. The following table shows how a student spends his pocket money during the course of a month. Represent it by a pie diagram.
| Items | Food | Entertainment | Other Expenditure | Savings |
| Expenditure | 40% | 25% | 20% | 15% |
Solution:
Here, total expenditure = 100%
So,
The central angle = (component value/100) × 360°
The central angle for each activity will be calculated as follows:
| Items | Expenditure | Central Angle |
| Food | 40% | 40/100 × 360° = 144 |
| Entertainment | 25% | 25/100 × 360° = 90 |
| Other Expenditure | 20% | 20/100 × 360° = 72 |
| Savings | 15% | 15/100 × 360° = 54 |
Now, the pie chart can be constructed by using the given data.
Steps to construct:
Step 1: Draw the circle of an appropriate radius.
Step 2: Draw a vertical radius anywhere inside the circle.
Step 3: Choose the largest central angle. Construct a sector of a central angle, whose one radius coincides with the radius drawn in step 2, and the other radius is in a clockwise direction to the vertical radius.
Step 4: Construct other sectors representing other values in a clockwise direction in descending order of magnitudes of their central angles.
Step 5: Shade the sectors so obtained by different colours and label them as shown in the below figure.
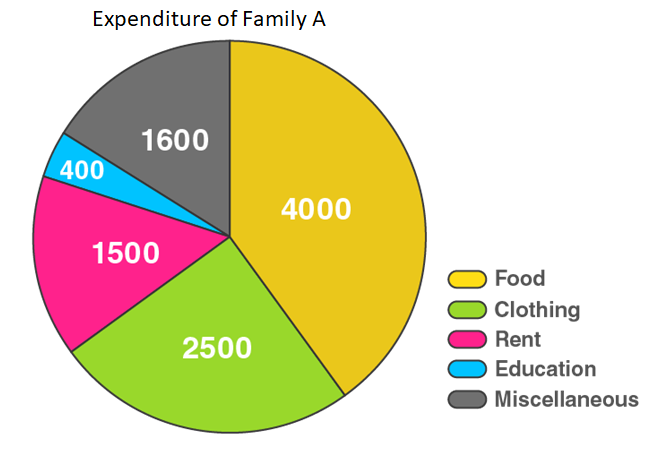
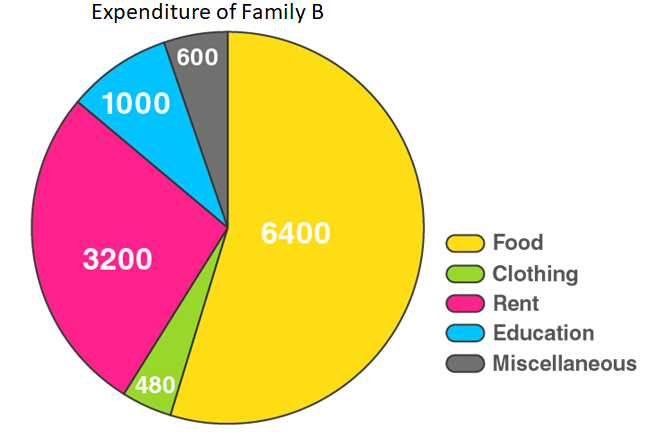
12. Represent the following data by a pie diagram:
| Items of Expenditure | Expenditure |
| Family A Family B | |
| Food | 4000 6400 |
| Clothing | 2500 480 |
| Rent | 1500 3200 |
| Education | 400 1000 |
| Miscellaneous | 1600 600 |
| Total | 10000 16000 |
Solution:
Here, the total expenditure of family A = 10000 and family B = 11680
The central angle for family A = (component value/10000) × 360°
The central angle for family B = (component value/11680) × 360°
Hence, the central angle for each activity will be calculated as follows:
| Items of expenditure | Expenditure of Family A | Expenditure of
Family B |
Central Angle of Family A | Central Angle of
Family B |
| Food | 4000 | 6400 | 4000/10000 × 360° = 144 | 6400/11680 × 360° = 197.3 |
| Clothing | 2500 | 480 | 2500/10000 × 360° = 90 | 480/11680 × 360° = 14.8 |
| Rent | 1500 | 3200 | 1500/10000 × 360° = 54 | 3200/11680 × 360° = 98.6 |
| Education | 400 | 1000 | 400/10000 × 360° = 14.4 | 1000/11680 × 360° = 30.8 |
| Miscellaneous | 1600 | 600 | 1600/10000 × 360° = 57.6 | 600/11680 × 360° = 18.5 |
Now, the pie chart for Family A and Family B can be constructed by using the given data.
Steps to construct:
Step 1: Draw the circle of an appropriate radius.
Step 2: Draw a vertical radius anywhere inside the circle.
Step 3: Choose the largest central angle. Construct a sector of a central angle, whose one radius coincides with the radius drawn in step 2, and the other radius is in a clockwise direction to the vertical radius.
Step 4: Construct other sectors representing other values in a clockwise direction in descending order of magnitudes of their central angles.
Step 5: Shade the sectors so obtained by different colours and label them as shown in the below figure.
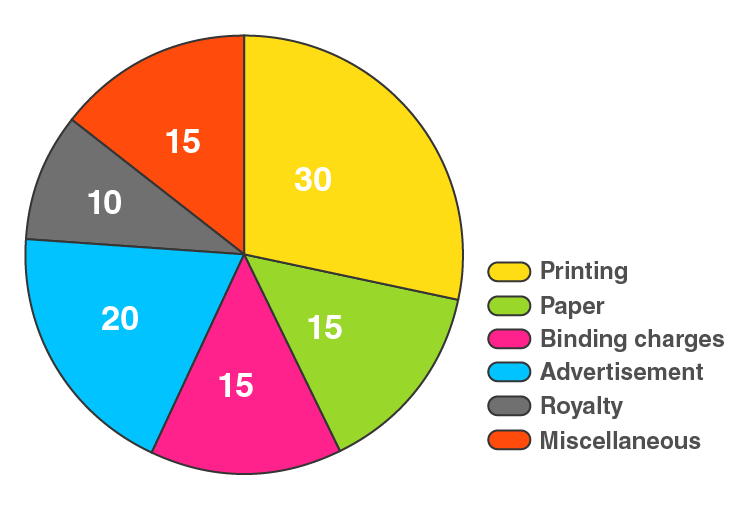
13. Following data gives a break up of the cost of production of a book:
| Printing | Paper | Binding Charges | Advertisement | Royalty | Miscellaneous |
| 30% | 15% | 15% | 20% | 10% | 15% |
Draw a pie diagram depicting the above information.
Solution:
Here, the total cost of production of the book = 105%
So,
The central angle = (component value/105) × 360°
The central angle for each activity will be calculated as follows:
| Items | Expenditure | Central Angle |
| Printing | 30% | 30/105 × 360° = 102.9 |
| Paper | 15% | 15/105 × 360° = 51.4 |
| Binding charges | 15% | 15/105 × 360° = 51.4 |
| Advertisement | 20% | 20/105 × 360° = 68.6 |
| Royalty | 10% | 10/105 × 360° = 34.3 |
| Miscellaneous | 15% | 15/105 × 360° = 51.4 |
Now, the pie chart can be constructed by using the given data.
Steps to construct:
Step 1: Draw the circle of an appropriate radius.
Step 2: Draw a vertical radius anywhere inside the circle.
Step 3: Choose the largest central angle. Construct a sector of a central angle, whose one radius coincides with the radius drawn in step 2, and the other radius is in a clockwise direction to the vertical radius.
Step 4: Construct other sectors representing other values in a clockwise direction in descending order of magnitudes of their central angles.
Step 5: Shade the sectors so obtained by different colours and label them as shown in the below figure.
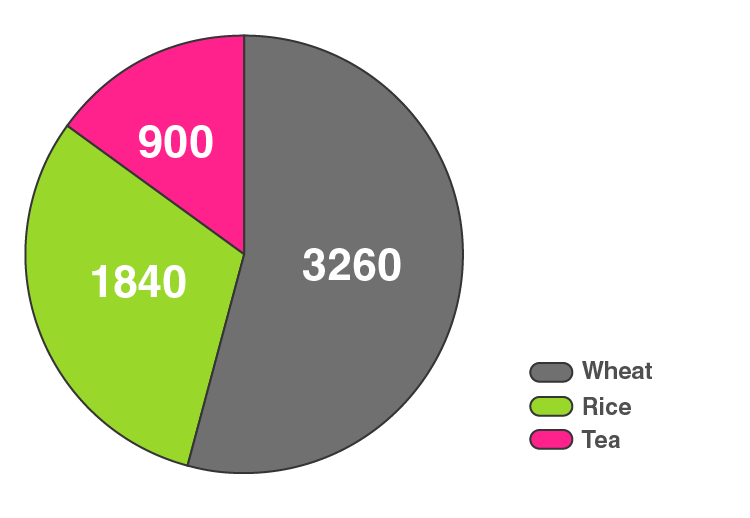
14. Represent the following data with the help of a pie diagram:
| Items | Wheat | Rice | Tea |
| Production (in metric tons) | 3260 | 1840 | 900 |
Solution:
Here, the total cost of production = 6000 metric tons
So,
The central angle = (component value/6000) × 360°
The central angle for each activity will be calculated as follows:
| Items | Production | Central angle |
| Wheat | 3260 | 3260/6000 × 360° = 195.6 |
| Rice | 1840 | 1840/6000 × 360° = 110.4 |
| Tea | 900 | 900/6000 × 360° = 54 |
Now, the pie chart can be constructed by using the given data.
Steps to construct:
Step 1: Draw the circle of an appropriate radius.
Step 2: Draw a vertical radius anywhere inside the circle.
Step 3: Choose the largest central angle. Construct a sector of a central angle, whose one radius coincides with the radius drawn in step 2, and the other radius is in a clockwise direction to the vertical radius.
Step 4: Construct other sectors representing other values in a clockwise direction in descending order of magnitudes of their central angles.
Step 5: Shade the sectors so obtained by different colours and label them as shown in the below figure.
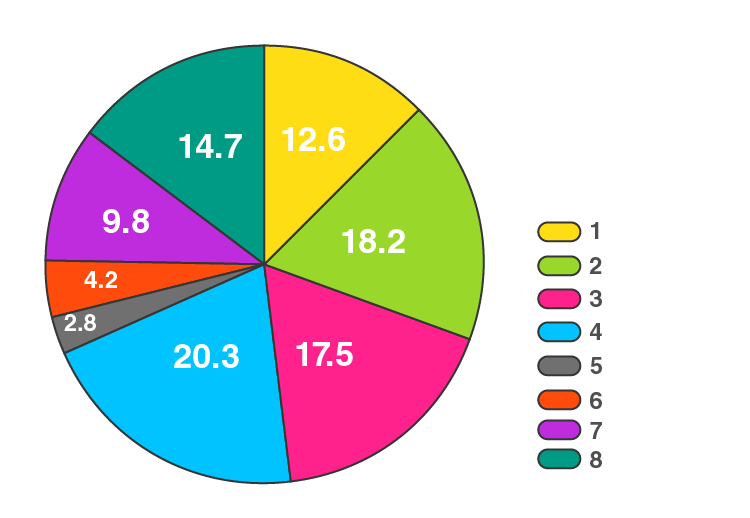
15. Draw a pie diagram representing the relative frequencies (expressed as percentages) of the eight classes as given below:
12.6, 18.2, 17.5, 20.3, 2.8, 4.2, 9.8, 14.7
Solution:
Here, total amount = 100.1%
So,
The central angle = (component value/100.1) × 360°
The central angle for each activity will be calculated as follows:
| Class | Amount (in %) | Central Angle |
| 1 | 12.6 | 12.6/100.1 × 360° = 45.3 |
| 2 | 18.2 | 18.2/100.1 × 360° = 65.5 |
| 3 | 17.5 | 17.5/100.1 × 360° = 62.9 |
| 4 | 20.3 | 20.3/100.1 × 360° = 73 |
| 5 | 2.8 | 2.8/100.1 × 360° = 10.1 |
| 6 | 4.2 | 4.2/100.1 × 360° = 15.1 |
| 7 | 9.8 | 9.8/100.1 × 360° = 35.2 |
| 8 | 14.7 | 14.7/100.1 × 360° = 52.9 |
Now, the pie chart can be constructed by using the given data.
Steps to construct:
Step 1: Draw the circle of an appropriate radius.
Step 2: Draw a vertical radius anywhere inside the circle.
Step 3: Choose the largest central angle. Construct a sector of a central angle, whose one radius coincides with the radius drawn in step 2, and the other radius is in a clockwise direction to the vertical radius.
Step 4: Construct other sectors representing other values in a clockwise direction in descending order of magnitudes of their central angles.
Step 5: Shade the sectors so obtained by different colours and label them as shown in the below figure.
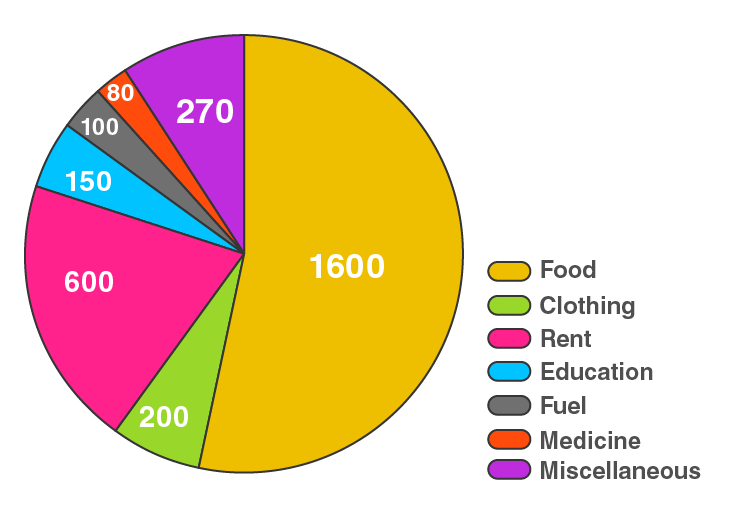
16. Following is the break up of the expenditure of a family on different items of consumption:
| Items | Food | Clothing | Rent | Education | Fuel etc. | Medicine | Miscellaneous |
| Expenditure (in Rs) | 1600 | 200 | 600 | 150 | 100 | 80 | 270 |
Draw a pie diagram to represent the above data.
Solution:
Here, total expenditure = Rs. 3000
So,
The central angle = (component value/3000) × 360°
The central angle for each activity will be calculated as follows:
| Items | Expenditure (in Rs) | Central angle |
| Food | 1600 | 1600/3000 × 360° = 192 |
| Clothing | 200 | 200/3000 × 360° = 24 |
| Rent | 600 | 600/3000 × 360° = 72 |
| Education | 150 | 150/3000 × 360° = 18 |
| Fuel | 100 | 100/3000 × 360° = 12 |
| Medicine | 80 | 80/3000 × 360° = 9.6 |
| Miscellaneous | 270 | 270/3000 × 360° = 32.4 |
Now, the pie chart can be constructed by using the given data.
Steps to construct:
Step 1: Draw the circle of an appropriate radius.
Step 2: Draw a vertical radius anywhere inside the circle.
Step 3: Choose the largest central angle. Construct a sector of a central angle, whose one radius coincides with the radius drawn in step 2, and the other radius is in a clockwise direction to the vertical radius.
Step 4: Construct other sectors representing other values in a clockwise direction in descending order of magnitudes of their central angles.
Step 5: Shade the sectors so obtained by different colours and label them as shown in the below figure.
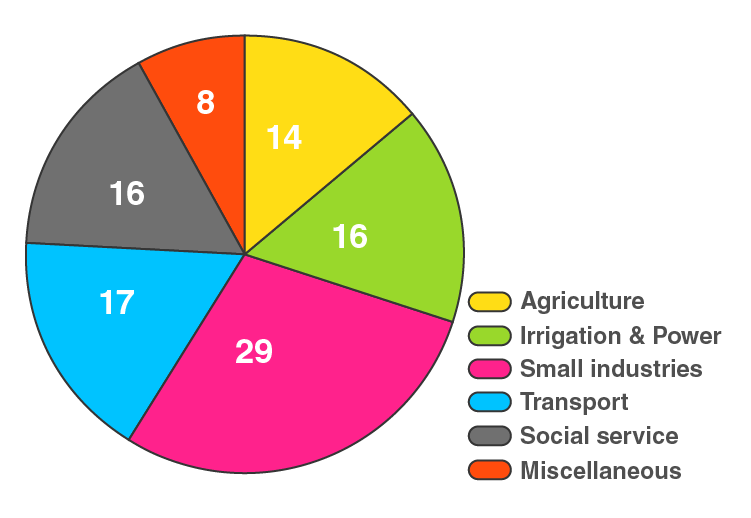
17. Draw a pie diagram for the following data of the investment pattern in a five years plan:
| Agriculture | Irrigation and Power | Small Industries | Transport | Social service | Miscellaneous |
| 14% | 16% | 29% | 17% | 16% | 8% |
Solution:
Here, total investment = 100%
So,
The central angle = (component value/100) × 360°
The central angle for each activity will be calculated as follows:
| Data | Investment | Central Angle |
| Agriculture | 14% | 14/100 × 360° = 50.4 |
| Irrigation and Power | 16% | 16/100 × 360° = 57.6 |
| Small Industries | 29% | 29/100 × 360° = 104.4 |
| Transport | 17% | 17/100 × 360° = 61.2 |
| Social service | 16% | 16/100 × 360° = 57.6 |
| Miscellaneous | 8% | 8/100 × 360° = 28.8 |
Now, the pie chart can be constructed by using the given data.
Steps to construct:
Step 1: Draw the circle of an appropriate radius.
Step 2: Draw a vertical radius anywhere inside the circle.
Step 3: Choose the largest central angle. Construct a sector of a central angle, whose one radius coincides with the radius drawn in step 2, and the other radius is in a clockwise direction to the vertical radius.
Step 4: Construct other sectors representing other values in a clockwise direction in descending order of magnitudes of their central angles.
Step 5: Shade the sectors so obtained by different colours and label them as shown in the below figure.


























Comments