NCERT Exemplar Solutions Class 10 Maths Chapter 10 – Free PDF Download
NCERT Exemplar Class 10 Maths Chapter 10 Constructions are available here in PDF, which can be downloaded easily for students. The problems and solutions are provided by our subject experts as per the latest CBSE syllabus (2023-2024) to help students prepare well for the board exam and score good marks. The solved questions in the exemplars provided here have been specifically designed to boost students’ knowledge about the topics and, at the same time, help them find the answers to all the important questions in this chapter. Students who solve Class 10 Maths Exemplars will be able to stay ahead in the class, as it is a great study tool.
These exemplars problems and solutions are designed by our expert faculty with respect to the latest CBSE syllabus, which covers the following topics of Chapter 10, Constructions:
- Dividing the line segment in a given ratio
- Construction of a similar triangle
- To construct tangents to a circle
When students go through the chapter “Constructions” in the Class 10 Maths textbook, they will basically explore new construction concepts which they should learn and master. Understanding this chapter is crucial as students will need to develop proper mathematical reasoning to discern why some constructions work and some don’t.
Download the PDF of NCERT Exemplar Solutions Class 10 Maths Chapter 10 Constructions
Access Answers to NCERT Exemplar Solutions for Class 10 Maths Chapter 10
Exercise 10.1 Page No: 114
Choose the correct answer from the given four options:
1. To divide a line segment AB in the ratio 5:7, first, a ray AX is drawn so that BAX is an acute angle, and then at equal distances, points are marked on the ray AX such that the minimum number of these points is
(A) 8 (B) 10 (C) 11 (D) 12
Solution:
(D) 12
According to the question,
A line segment AB in the ratio 5:7
So, A:B = 5:7
Now,
Draw a ray AX making an acute angle ∠BAX,
Mark A+B points at equal distance.
So, we have A=5 and B=7
Hence, minimum number of these points = A+B = 5+7 =12
2. To divide a line segment AB in the ratio 4:7, a ray AX is drawn first such that BAX is an acute angle and then points A1, A2, A3,…. are located at equal distances on the ray AX, and the point B is joined to
(A) A12 (B) A11 (C) A10 (D) A9
Solution:
(B) A11
According to the question,
A line segment AB in the ratio 4:7
So, A:B = 4:7
Now,
Draw a ray AX making an acute angle BAX
Minimum number of points located at equal distances on the ray,
AX = A+B = 4+7= 11
A1, A2, A3, ………. are located at equal distances on the ray AX.
Point B is joined to the last point is A11.
3. To divide a line segment AB in the ratio 5 : 6, draw a ray AX such that ∠BAX is an acute angle, then draw a ray BY parallel to AX and the points A1, A2, A3, … and B1, B2, B3, … are located at equal distances on ray AX and BY, respectively. Then the points joined are
(A) A5 and B6 (B) A6 and B5 (C) A4 and B5 (D) A5 and B4
Solution:
(A) A5 and B6
According to the question,
A line segment AB in the ratio 5:7
So, A:B = 5:7
Steps of construction:
1. Draw a ray AX, an acute angle BAX.
2. Draw a ray BY ||AX, angle ABY = angle BAX.
3. Now, locate the points A1,A2,A3,A4 and A5 on AX and B1,B2,B3,B4,B5 and B6
(Because A:B = 5:7)
4. Join A5B6.
A5B6 intersect AB at a point C.
AC:BC= 5:6

Exercise 10.2 Page No: 115
Write True or False and give reasons for your answer in each of the following:
1. By geometrical construction, it is possible to divide a line segment in the ratio √3:(1/√3)
Solution:
True
Justification:
According to the question,
Ratio= √3 : ( 1/√3)
On simplifying we get,
√3/ (1/√3) = (√3 x √3)/1 = 3:1
Required ratio = 3:1
Hence,
Geometrical construction is possible to divide a line segment in the ratio 3:1.
2. To construct a triangle similar to a given △ABC with its sides 7/3 of the corresponding sides of △ABC, draw a ray BX making an acute angle with BC and X lying on the opposite side of A with respect to BC. The points B1, B2, …., B7 are located at equal distances on BX, B3 is joined to C, and then a line segment B6C‘ is drawn parallel to B3C where C‘ lies on BC produced. Finally, line segment A‘C‘ is drawn parallel to AC.
Solution:
False
Justification:
Let us try to construct the figure as given in the question.
Steps of construction,
1. Draw a line segment BC.
2. With B and C as centres, draw two arcs of suitable radius intersecting each other at A.
3. Join BA and CA and we get the required triangle ∆ABC.
4. Draw a ray BX from B downwards to make an acute angle ∠CBX.
5. Now, mark seven points B1, B2, B3 …B7 on BX, such that BB1 = B1B2 = B2B3 = B3B4 = B4B5 = B5B6 = B6B7.
6. Join B3C and draw a line B7C’|| B3C from B7 such that it intersects the extended line segment BC at C’.
7. Draw C’A’ ||CA in such a way that it intersects the extended line segment BA at A’.
Then, ∆A’BC’ is the required triangle whose sides are 7/3 of the corresponding sides of
∆ABC.
According to the question,
We have,
Segment B6C’ || B3C. But it is clear in our construction that it is never possible that segment B6C’||B3C since the similar triangle A’BC’ has its sides 7/3 of the corresponding sides of triangle ABC.
So, B7C’ is parallel to B3C.
Exercise 10.3 Page No: 116
1. Draw a line segment of length 7 cm. Find a point P on it which divides it in the ratio 3:5.
Solution:

Steps of construction:
1. Draw a line segment, AB = 7 cm.
2. Draw a ray, AX, making an acute angle down ward with AB.
3. Mark the points A1, A2, A3 … A8 on AX.
4. Mark the points such that AA1 = A1A2 = A2A3 = ….., A7A8.
5. Join BA8.
6. Draw a line parallel to BA8 through the point A3, to meet AB on P.
Hence AP: PB = 3: 5
2. Draw a right triangle ABC in which BC = 12 cm, AB = 5 cm and ∠B = 90°. Construct a triangle similar to it and of scale factor 2/3. Is the new triangle also a right triangle?
Solution:

Steps of construction:
1. Draw a line segment AB = 5 cm. Construct a right angle SAB at point A.
2. Draw an arc of radius 12 cm with B as its centre to intersect SA at C.
3. Join BC to obtain ABC.
4. Draw a ray AX making an acute angle with AB, opposite to vertex C.
5. Locate 3 points, A1, A2, A3 on line segment AX such that AA1 = A1A2 = A2A3.
6. Join A3B.
7. Draw a line through A2 parallel to A3B intersecting AB at B’.
8. Through B’, draw a line parallel to BC intersecting AC at C’.
9. Triangle AB’C’ is the required triangle.
Exercise 10.4 Page No: 117
1. Two line segments AB and AC include an angle of 60° where AB = 5 cm and AC = 7 cm. Locate points P and Q on AB and AC, respectively such that AP = ¾ AB and AQ = ¼ AC. Join P and Q and measure the length PQ.
Solution:
Steps of construction:
1. Draw a line segment AB = 5 cm.

2. Draw ∠BAZ = 60°.
3. With centre A and radius 7 cm, draw an arc cutting the line AZ at C.
4. Draw a ray AX, making an acute ∠BAX.
5. Divide AX into four equal parts, namely AA1 = A1A2 = A2A3 = A3A4.
6. Join A4B.
7. Draw A3P || A4B meeting AB at P.
8. Hence, we obtain, P is the point on AB such that AP = ¾ AB.
9. Next, draw a ray AY, such that it makes an acute ∠CAY.
10. Divide AY into four parts, namely AB1 = B1B2 = B2B3 = B3B4.
11. Join B4C.
12. Draw B1Q || B4C meeting AC at Q. We get, Q is the point on AC such that AQ = ¼ AC.
13. Join PQ and measure it.
14. PQ = 3.25 cm.
2. Draw a parallelogram ABCD in which BC = 5 cm, AB = 3 cm and angle ABC = 60°, divide it into triangles BCD and ABD by the diagonal BD. Construct the triangle BD‘ C‘ similar to triangle BDC with scale factor 4/3. Draw the line segment D‘A‘ parallel to DA where A’ lies on extended side BA. Is A’BC’D’ a parallelogram?
Solution:
Steps of constructions:
1. Draw a line AB=3 cm.
2. Draw a ray BY making an acute ∠ABY=60°.
3. With centre B and radius 5 cm, draw an arc cutting the point C on BY.
4. Draw a ray AZ making an acute ∠ZAX’=60°.(BY||AZ, ∴ ∠YBX’=ZAX’=60°)
5. With centre A and radius 5 cm, draw an arc cutting the point D on AZ.
6. Join CD
7. Thus we obtain a parallelogram ABCD.
8. Join BD, the diagonal of parallelogram ABCD.
9. Draw a ray BX downwards making an acute ∠CBX.
10. Locate 4 points B1, B2, B3, B4 on BX, such that BB1=B1B2=B2B3=B3B4.
11. Join B4C and from B3C draw a line B4C’||B3C intersecting the extended line segment BC at C’.
12. Draw C’D’|| CD intersecting the extended line segment BD at D’. Then, ∆D’BC’ is the required triangle whose sides are 4/3 of the corresponding sides of ∆DBC.
13. Now draw a line segment D’A’|| DA, where A’ lies on the extended side BA.
14. Finally, we observe that A’BC’D’ is a parallelogram in which A’D’=6.5 cm A’B = 4 cm and ∠A’BD’= 60° divide it into triangles BC’D’ and A’BD’ by the diagonal BD’.

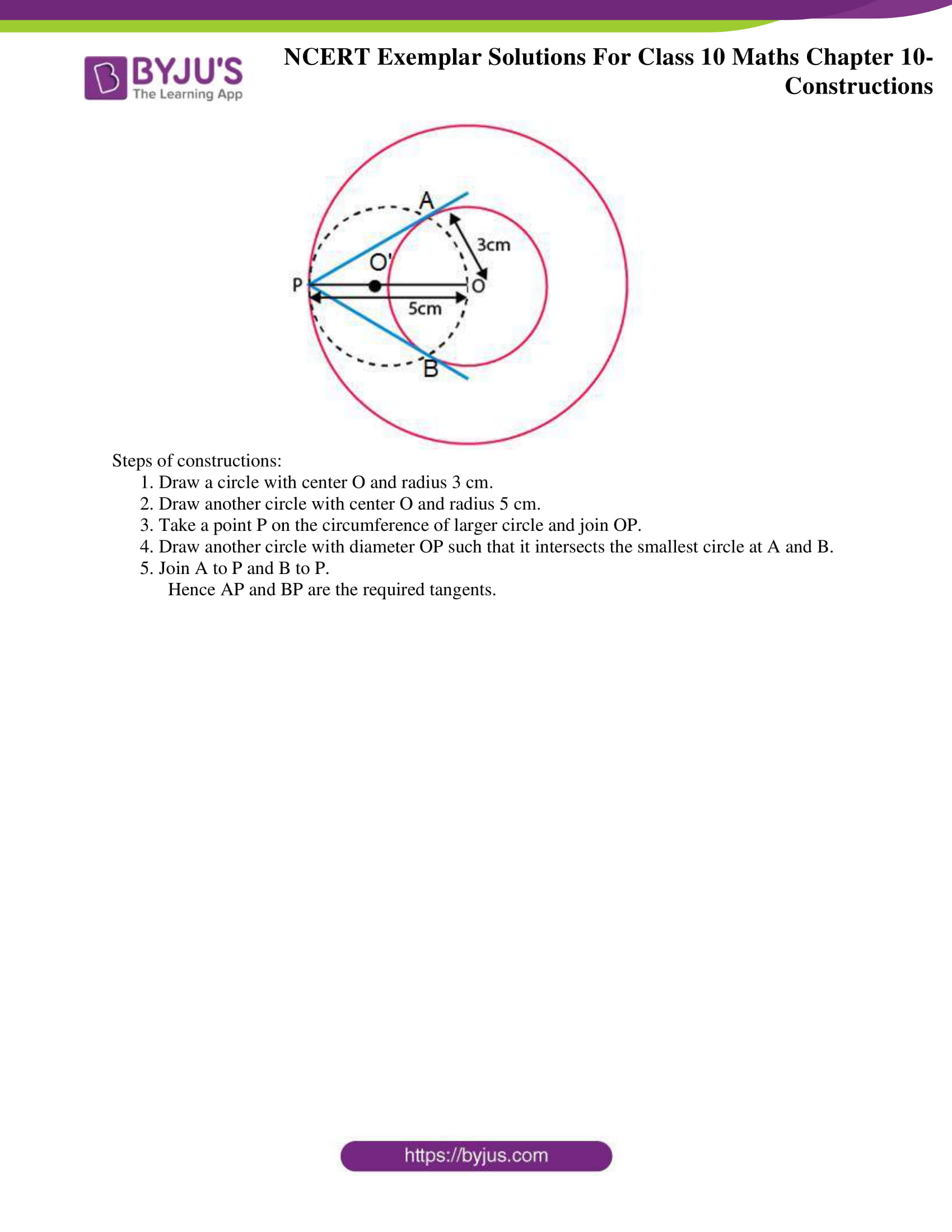
3. Draw two concentric circles of radii 3 cm and 5 cm. Taking a point on outer circle construct the pair of tangents to the other. Measure the length of a tangent and verify it by actual calculation.
Solution:

Steps of constructions:
1. Draw a circle with centre O and radius 3 cm.
2. Draw another circle with centre O and radius 5 cm.
3. Take a point P on the circumference of larger circle and join OP.
4. Draw another circle with diameter OP such that it intersects the smallest circle at A and B.
5. Join A to P and B to P.
Hence AP and BP are the required tangents.
| Also Access |
| NCERT Solutions for Class 10 Maths Chapter 10 |
| CBSE Notes for Class 10 Maths Chapter 10 |
In order to help students get a clear insight into the concepts of constructions and get familiar with some of the methods of solving problems, free NCERT Exemplar Solutions for Class 10 Maths Chapter 10 are provided here. To help students practise thoroughly for the board exam, BYJU’S also provides online learning materials such as notes, exemplar books, NCERT Maths Solutions for Class 10 and question papers, which they can make the best use of it. Students are also recommended that they solve sample papers and previous years’ question papers to get an idea of the type of questions asked from Chapter 10, Constructions.
Solved Exemplars for Class 10 are available at BYJU’S for Maths and Science subjects. Download BYJU’S – The Learning App to get personalised videos explaining different types of Maths topics such as Constructions, Circle, Triangles, etc. and experience a new approach to learning to understand the concepts in an easy way. Also, with the preparation tips and tricks available here, you can solve difficult problems quickly.
Frequently Asked Questions on NCERT Exemplar Solutions for Class 10 Maths Chapter 10
How many questions are present in each exercise of NCERT Exemplar Solutions for Class 10 Maths Chapter 10?
Exercise 10.1 – 3 Questions
Exercise 10.2 – 2 Questions
Exercise 10.3 – 2 Questions
Exercise 10.4 – 3 Questions
What are the major concepts discussed in NCERT Exemplar Solutions for Class 10 Maths Chapter 10?
1. Dividing the line segment in a given ratio
2. Construction of a similar triangle
3. To construct tangents to a circle
Where can I get exercise-wise answers to NCERT Exemplar Solutions for Class 10 Maths Chapter 10?
Also, Read








Comments