RD Sharma Solutions Class 11 Maths Chapter 14 – Download Free PDF Updated Session 2023 – 24
RD Sharma Solutions for Class 11 Maths Chapter 14 – Quadratic Equations are provided here to help students study and score good marks in the board exams. In earlier classes, students studied quadratic equations with real coefficients and real roots only. In this chapter, we shall see quadratic equations with real coefficients and complex roots. The chapter also discusses quadratic equations with complex coefficients and their solutions in the complex number system. RD Sharma Class 11 Maths Solutions PDF can be downloaded from the links provided below.
Chapter 14 – Quadratic Equations contains two exercises, and RD Sharma Solutions offers detailed solutions to the questions present in each exercise. For a better understanding of the concepts, students can solve the exercise-wise problems using the RD Sharma Solutions, which are developed by our expert faculty team at BYJU’S. Students aspiring to secure high marks in their examinations are advised to practise the solutions on a regular basis. Now, let us have a look at the concepts discussed in this chapter.
- Some useful definitions and results.
- Quadratic equations with real coefficients.
- Quadratic equations with complex coefficients.
RD Sharma Solutions for Class 11 Maths Chapter 14 – Quadratic Equations
Access answers to RD Sharma Solutions for Class 11 Maths Chapter 14 – Quadratic Equations
EXERCISE 14.1 PAGE NO: 14.5
Solve the following quadratic equations by factorisation method only:
1. x2 + 1 = 0
Solution:
Given: x2 + 1 = 0
We know, i2 = –1 ⇒ 1 = –i2
By substituting 1 = –i2 in the above equation, we get
x2 – i2 = 0
[By using the formula, a2 – b2 = (a + b) (a – b)](x + i) (x – i) = 0
x + i = 0 or x – i = 0
x = –i or x = i
∴ The roots of the given equation are i, -i
2. 9x2 + 4 = 0
Solution:
Given: 9x2 + 4 = 0
9x2 + 4 × 1 = 0
We know, i2 = –1 ⇒ 1 = –i2
By substituting 1 = –i2 in the above equation, we get
So,
9x2 + 4(–i2) = 0
9x2 – 4i2 = 0
(3x)2 – (2i)2 = 0
[By using the formula, a2 – b2 = (a + b) (a – b)](3x + 2i) (3x – 2i) = 0
3x + 2i = 0 or 3x – 2i = 0
3x = –2i or 3x = 2i
x = -2i/3 or x = 2i/3
∴ The roots of the given equation are 2i/3, -2i/3
3. x2 + 2x + 5 = 0
Solution:
Given: x2 + 2x + 5 = 0
x2 + 2x + 1 + 4 = 0
x2 + 2(x) (1) + 12 + 4 = 0
(x + 1)2 + 4 = 0 [since, (a + b)2 = a2 + 2ab + b2]
(x + 1)2 + 4 × 1 = 0
We know, i2 = –1 ⇒ 1 = –i2
By substituting 1 = –i2 in the above equation, we get
(x + 1)2 + 4(–i2) = 0
(x + 1)2 – 4i2 = 0
(x + 1)2 – (2i)2 = 0
[By using the formula, a2 – b2 = (a + b) (a – b)](x + 1 + 2i)(x + 1 – 2i) = 0
x + 1 + 2i = 0 or x + 1 – 2i = 0
x = –1 – 2i or x = –1 + 2i
∴ The roots of the given equation are -1+2i, -1-2i
4. 4x2 – 12x + 25 = 0
Solution:
Given: 4x2 – 12x + 25 = 0
4x2 – 12x + 9 + 16 = 0
(2x)2 – 2(2x)(3) + 32 + 16 = 0
(2x – 3)2 + 16 = 0 [Since, (a + b)2 = a2 + 2ab + b2]
(2x – 3)2 + 16 × 1 = 0
We know, i2 = –1 ⇒ 1 = –i2
By substituting 1 = –i2 in the above equation, we get
(2x – 3)2 + 16(–i2) = 0
(2x – 3)2 – 16i2 = 0
(2x – 3)2 – (4i)2 = 0
[By using the formula, a2 – b2 = (a + b) (a – b)](2x – 3 + 4i) (2x – 3 – 4i) = 0
2x – 3 + 4i = 0 or 2x – 3 – 4i = 0
2x = 3 – 4i or 2x = 3 + 4i
x = 3/2 – 2i or x = 3/2 + 2i
∴ The roots of the given equation are 3/2 + 2i, 3/2 – 2i
5. x2 + x + 1 = 0
Solution:
Given: x2 + x + 1 = 0
x2 + x + ¼ + ¾ = 0
x2 + 2 (x) (1/2) + (1/2)2 + ¾ = 0
(x + 1/2)2 + ¾ = 0 [Since, (a + b)2 = a2 + 2ab + b2]
(x + 1/2)2 + ¾ × 1 = 0
We know, i2 = –1 ⇒ 1 = –i2
By substituting 1 = –i2 in the above equation, we get
(x + ½)2 + ¾ (-1)2 = 0
(x + ½)2 + ¾ i2 = 0
(x + ½)2 – (√3i/2)2 = 0
[By using the formula, a2 – b2 = (a + b) (a – b)](x + ½ + √3i/2) (x + ½ – √3i/2) = 0
(x + ½ + √3i/2) = 0 or (x + ½ – √3i/2) = 0
x = -1/2 – √3i/2 or x = -1/2 + √3i/2
∴ The roots of the given equation are -1/2 + √3i/2, -1/2 – √3i/2
6. 4x2 + 1 = 0
Solution:
Given: 4x2 + 1 = 0
We know, i2 = –1 ⇒ 1 = –i2
By substituting 1 = –i2 in the above equation, we get
4x2 – i2 = 0
(2x)2 – i2 = 0
[By using the formula, a2 – b2 = (a + b) (a – b)](2x + i) (2x – i) = 0
2x + i = 0 or 2x – i = 0
2x = –i or 2x = i
x = -i/2 or x = i/2
∴ The roots of the given equation are i/2, -i/2
7. x2 – 4x + 7 = 0
Solution:
Given: x2 – 4x + 7 = 0
x2 – 4x + 4 + 3 = 0
x2 – 2(x) (2) + 22 + 3 = 0
(x – 2)2 + 3 = 0 [Since, (a – b)2 = a2 – 2ab + b2]
(x – 2)2 + 3 × 1 = 0
We know, i2 = –1 ⇒ 1 = –i2
By substituting 1 = –i2 in the above equation, we get
(x – 2)2 + 3(–i2) = 0
(x – 2)2 – 3i2 = 0
(x – 2)2 – (√3i)2 = 0
[By using the formula, a2 – b2 = (a + b) (a – b)](x – 2 + √3i) (x – 2 – √3i) = 0
(x – 2 + √3i) = 0 or (x – 2 – √3i) = 0
x = 2 – √3i or x = 2 + √3i
x = 2 ± √3i
∴ The roots of the given equation are 2 ± √3i
8. x2 + 2x + 2 = 0
Solution:
Given: x2 + 2x + 2 = 0
x2 + 2x + 1 + 1 = 0
x2 + 2(x)(1) + 12 + 1 = 0
(x + 1)2 + 1 = 0 [∵ (a + b)2 = a2 + 2ab + b2]
We know, i2 = –1 ⇒ 1 = –i2
By substituting 1 = –i2 in the above equation, we get
(x + 1)2 + (–i2) = 0
(x + 1)2 – i2 = 0
(x + 1)2 – (i)2 = 0
[By using the formula, a2 – b2 = (a + b) (a – b)](x + 1 + i) (x + 1 – i) = 0
x + 1 + i = 0 or x + 1 – i = 0
x = –1 – i or x = –1 + i
x = -1 ± i
∴ The roots of the given equation are -1 ± i
9. 5x2 – 6x + 2 = 0
Solution:
Given: 5x2 – 6x + 2 = 0
We shall apply the discriminant rule.
Where, x = (-b ±√(b2 – 4ac))/2a
Here, a = 5, b = -6, c = 2
So,
x = (-(-6) ±√(-62 – 4 (5)(2)))/ 2(5)
= (6 ± √(36-40))/10
= (6 ± √(-4))/10
= (6 ± √4(-1))/10
We have i2 = –1
By substituting –1 = i2 in the above equation, we get
x = (6 ± √4i2)/10
= (6 ± 2i)/10
= 2(3±i)/10
= (3±i)/5
x = 3/5 ± i/5
∴ The roots of the given equation are 3/5 ± i/5
10. 21x2 + 9x + 1 = 0
Solution:
Given: 21x2 + 9x + 1 = 0
We shall apply the discriminant rule.
Where, x = (-b ±√(b2 – 4ac))/2a
Here, a = 21, b = 9, c = 1
So,
x = (-9 ±√(92 – 4 (21)(1)))/ 2(21)
= (-9 ± √(81-84))/42
= (-9 ± √(-3))/42
= (-9 ± √3(-1))/42
We have i2 = –1
By substituting –1 = i2 in the above equation, we get
x = (-9 ± √3i2)/42
= (-9 ± √(√3i)2/42
= (-9 ± √3i)/42
= -9/42 ± √3i/42
= -3/14 ± √3i/42
∴ The roots of the given equation are -3/14 ± √3i/42
11. x2 – x + 1 = 0
Solution:
Given: x2 – x + 1 = 0
x2 – x + ¼ + ¾ = 0
x2 – 2 (x) (1/2) + (1/2)2 + ¾ = 0
(x – 1/2)2 + ¾ = 0 [Since, (a + b)2 = a2 + 2ab + b2]
(x – 1/2)2 + ¾ × 1 = 0
We know, i2 = –1 ⇒ 1 = –i2
By substituting 1 = –i2 in the above equation, we get
(x – ½)2 + ¾ (-1)2 = 0
(x – ½)2 + ¾ (-i)2 = 0
(x – ½)2 – (√3i/2)2 = 0
[By using the formula, a2 – b2 = (a + b) (a – b)](x – ½ + √3i/2) (x – ½ – √3i/2) = 0
(x – ½ + √3i/2) = 0 or (x – ½ – √3i/2) = 0
x = 1/2 – √3i/2 or x = 1/2 + √3i/2
∴ The roots of the given equation are 1/2 + √3i/2, 1/2 – √3i/2
12. x2 + x + 1 = 0
Solution:
Given: x2 + x + 1 = 0
x2 + x + ¼ + ¾ = 0
x2 + 2 (x) (1/2) + (1/2)2 + ¾ = 0
(x + 1/2)2 + ¾ = 0 [Since, (a + b)2 = a2 + 2ab + b2]
(x + 1/2)2 + ¾ × 1 = 0
We know, i2 = –1 ⇒ 1 = –i2
By substituting 1 = –i2 in the above equation, we get
(x + ½)2 + ¾ (-1)2 = 0
(x + ½)2 + ¾ i2 = 0
(x + ½)2 – (√3i/2)2 = 0
[By using the formula, a2 – b2 = (a + b) (a – b)](x + ½ + √3i/2) (x + ½ – √3i/2) = 0
(x + ½ + √3i/2) = 0 or (x + ½ – √3i/2) = 0
x = -1/2 – √3i/2 or x = -1/2 + √3i/2
∴ The roots of the given equation are -1/2 + √3i/2, -1/2 – √3i/2
13. 17x2 – 8x + 1 = 0
Solution:
Given: 17x2 – 8x + 1 = 0
We shall apply the discriminant rule.
Where, x = (-b ±√(b2 – 4ac))/2a
Here, a = 17, b = -8, c = 1
So,
x = (-(-8) ±√(-82 – 4 (17)(1)))/ 2(17)
= (8 ± √(64-68))/34
= (8 ± √(-4))/34
= (8 ± √4(-1))/34
We have i2 = –1
By substituting –1 = i2 in the above equation, we get
x = (8 ± √(2i)2)/34
= (8 ± 2i)/34
= 2(4±i)/34
= (4±i)/17
x = 4/17 ± i/17
∴ The roots of the given equation are 4/17 ± i/17
EXERCISE 14.2 PAGE NO: 14.13
1. Solving the following quadratic equations by factorisation method:
(i) x2 + 10ix – 21 = 0
(ii) x2 + (1 – 2i)x – 2i = 0
(iii) x2 – (2√3 + 3i) x + 6√3i = 0
(iv) 6x2 – 17ix – 12 = 0
Solution:
(i) x2 + 10ix – 21 = 0
Given: x2 + 10ix – 21 = 0
x2 + 10ix – 21 × 1 = 0
We know, i2 = –1 ⇒ 1 = –i2
By substituting 1 = –i2 in the above equation, we get
x2 + 10ix – 21(–i2) = 0
x2 + 10ix + 21i2 = 0
x2 + 3ix + 7ix + 21i2 = 0
x(x + 3i) + 7i(x + 3i) = 0
(x + 3i) (x + 7i) = 0
x + 3i = 0 or x + 7i = 0
x = –3i or –7i
∴ The roots of the given equation are –3i, –7i
(ii) x2 + (1 – 2i)x – 2i = 0
Given: x2 + (1 – 2i)x – 2i = 0
x2 + x – 2ix – 2i = 0
x(x + 1) – 2i(x + 1) = 0
(x + 1) (x – 2i) = 0
x + 1 = 0 or x – 2i = 0
x = –1 or 2i
∴ The roots of the given equation are –1, 2i
(iii) x2 – (2√3 + 3i) x + 6√3i = 0
Given: x2 – (2√3 + 3i) x + 6√3i = 0
x2 – (2√3x + 3ix) + 6√3i = 0
x2 – 2√3x – 3ix + 6√3i = 0
x(x – 2√3) – 3i(x – 2√3) = 0
(x – 2√3) (x – 3i) = 0
(x – 2√3) = 0 or (x – 3i) = 0
x = 2√3 or x = 3i
∴ The roots of the given equation are 2√3, 3i
(iv) 6x2 – 17ix – 12 = 0
Given: 6x2 – 17ix – 12 = 0
6x2 – 17ix – 12 × 1 = 0
We know, i2 = –1 ⇒ 1 = –i2
By substituting 1 = –i2 in the above equation, we get
6x2 – 17ix – 12(–i2) = 0
6x2 – 17ix + 12i2 = 0
6x2 – 9ix – 8ix + 12i2 = 0
3x(2x – 3i) – 4i(2x – 3i) = 0
(2x – 3i) (3x – 4i) = 0
2x – 3i = 0 or 3x – 4i = 0
2x = 3i or 3x = 4i
x = 3i/2 or x = 4i/3
∴ The roots of the given equation are 3i/2, 4i/3
2. Solve the following quadratic equations:
(i) x2 – (3√2 + 2i) x + 6√2i = 0
(ii) x2 – (5 – i) x + (18 + i) = 0
(iii) (2 + i)x2 – (5- i)x + 2 (1 – i) = 0
(iv) x2 – (2 + i)x – (1 – 7i) = 0
(v) ix2 – 4x – 4i = 0
(vi) x2 + 4ix – 4 = 0
(vii) 2x2 + √15ix – i = 0
(viii) x2 – x + (1 + i) = 0
(ix) ix2 – x + 12i = 0
(x) x2 – (3√2 – 2i)x – √2i = 0
(xi) x2 – (√2 + i)x + √2i = 0
(xii) 2x2 – (3 + 7i)x + (9i – 3) = 0
Solution:
(i) x2 – (3√2 + 2i) x + 6√2i = 0
Given: x2 – (3√2 + 2i) x + 6√2i = 0
x2 – (3√2x + 2ix) + 6√2i = 0
x2 – 3√2x – 2ix + 6√2i = 0
x(x – 3√2) – 2i(x – 3√2) = 0
(x – 3√2) (x – 2i) = 0
(x – 3√2) = 0 or (x – 2i) = 0
x = 3√2 or x = 2i
∴ The roots of the given equation are 3√2, 2i
(ii) x2 – (5 – i) x + (18 + i) = 0
Given: x2 – (5 – i) x + (18 + i) = 0
We shall apply the discriminant rule.
Where, x = (-b ±√(b2 – 4ac))/2a
Here, a = 1, b = -(5-i), c = (18+i)
So,
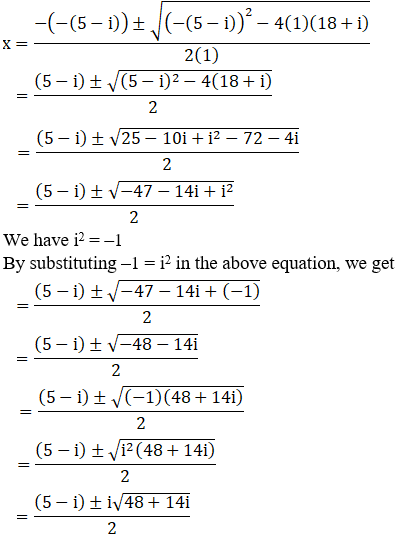
We can write 48 + 14i = 49 – 1 + 14i
So,
48 + 14i = 49 + i2 + 14i [∵ i2 = –1]
= 72 + i2 + 2(7)(i)
= (7 + i)2 [Since, (a + b)2 = a2 + b2 + 2ab]
By using the result 48 + 14i = (7 + i) 2, we get
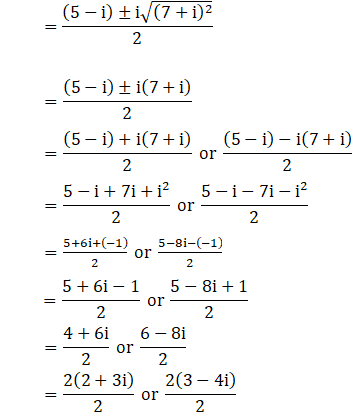
x = 2 + 3i or 3 – 4i
∴ The roots of the given equation are 3 – 4i, 2 + 3i
(iii) (2 + i)x2 – (5- i)x + 2 (1 – i) = 0
Given: (2 + i)x2 – (5- i)x + 2 (1 – i) = 0
We shall apply the discriminant rule.
Where, x = (-b ±√(b2 – 4ac))/2a
Here, a = (2+i), b = -(5-i), c = 2(1-i)
So,
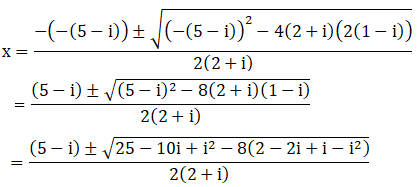
We have i2 = –1
By substituting –1 = i2 in the above equation, we get
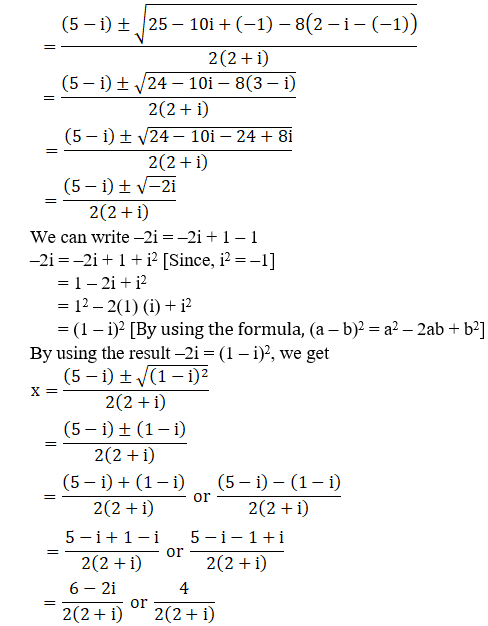
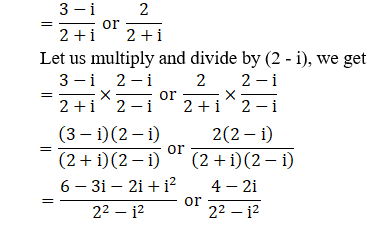
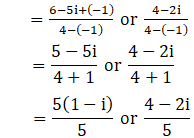
x = (1 – i) or 4/5 – 2i/5
∴ The roots of the given equation are (1 – i), 4/5 – 2i/5
(iv) x2 – (2 + i)x – (1 – 7i) = 0
Given: x2 – (2 + i)x – (1 – 7i) = 0
We shall apply the discriminant rule.
Where, x = (-b ±√(b2 – 4ac))/2a
Here, a = 1, b = -(2+i), c = -(1-7i)
So,
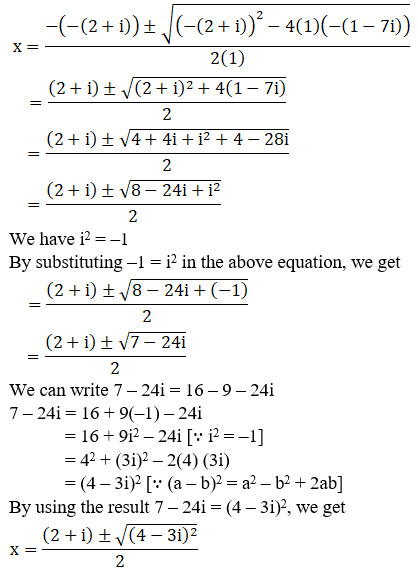
We can write 7 – 24i = 16 – 9 – 24i
7 – 24i = 16 + 9(–1) – 24i
= 16 + 9i2 – 24i [∵ i2 = –1]
= 42 + (3i)2 – 2(4) (3i)
= (4 – 3i)2 [∵ (a – b)2 = a2 – b2 + 2ab]
By using the result 7 – 24i = (4 – 3i)2, we get
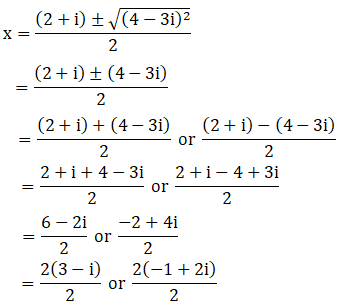
x = 3 – i or -1 + 2i
∴ The roots of the given equation are (-1 + 2i), (3 – i)
(v) ix2 – 4x – 4i = 0
Given: ix2 – 4x – 4i = 0
ix2 + 4x(–1) – 4i = 0 [We know, i2 = –1]
So by substituting –1 = i2 in the above equation, we get
ix2 + 4xi2 – 4i = 0
i(x2 + 4ix – 4) = 0
x2 + 4ix – 4 = 0
x2 + 4ix + 4(–1) = 0
x2 + 4ix + 4i2 = 0 [Since, i2 = –1]
x2 + 2ix + 2ix + 4i2 = 0
x(x + 2i) + 2i(x + 2i) = 0
(x + 2i) (x + 2i) = 0
(x + 2i)2 = 0
x + 2i = 0
x = –2i, -2i
∴ The roots of the given equation are –2i, –2i
(vi) x2 + 4ix – 4 = 0
Given: x2 + 4ix – 4 = 0
x2 + 4ix + 4(–1) = 0 [We know, i2 = –1]
So by substituting –1 = i2 in the above equation, we get
x2 + 4ix + 4i2 = 0
x2 + 2ix + 2ix + 4i2 = 0
x(x + 2i) + 2i(x + 2i) = 0
(x + 2i) (x + 2i) = 0
(x + 2i)2 = 0
x + 2i = 0
x = –2i, -2i
∴ The roots of the given equation are –2i, –2i
(vii) 2x2 + √15ix – i = 0
Given: 2x2 + √15ix – i = 0
We shall apply the discriminant rule.
Where, x = (-b ±√(b2 – 4ac))/2a
Here, a = 2, b = √15i, c = -i
So,
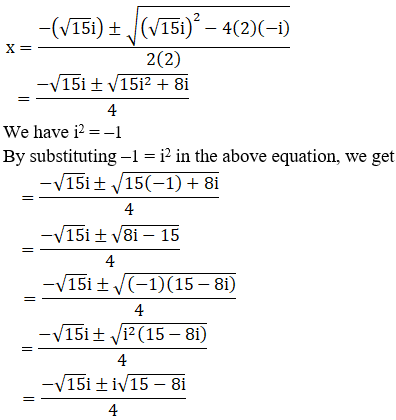
We can write 15 – 8i = 16 – 1 – 8i
15 – 8i = 16 + (–1) – 8i
= 16 + i2 – 8i [∵ i2 = –1]
= 42 + (i)2 – 2(4)(i)
= (4 – i)2 [Since, (a – b)2 = a2 – b2 + 2ab]
By using the result 15 – 8i = (4 – i)2, we get
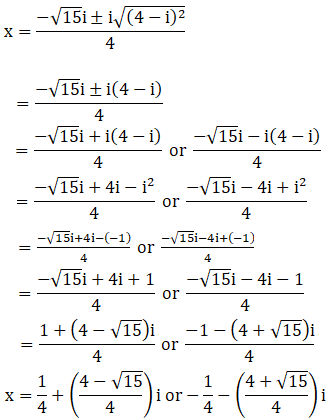
∴ The roots of the given equation are [1+ (4 – √15)i/4] , [-1 -(4 + √15)i/4]
(viii) x2 – x + (1 + i) = 0
Given: x2 – x + (1 + i) = 0
We shall apply the discriminant rule.
Where, x = (-b ±√(b2 – 4ac))/2a
Here, a = 1, b = -1, c = (1+i)
So,
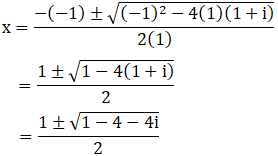
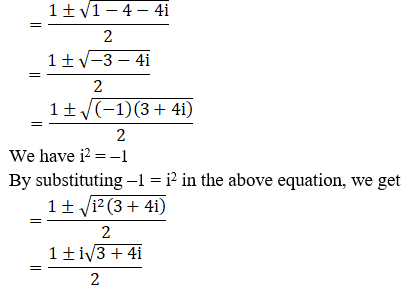
We can write 3 + 4i = 4 – 1 + 4i
3 + 4i = 4 + i2 + 4i [∵ i2 = –1]
= 22 + i2 + 2(2) (i)
= (2 + i)2 [Since, (a + b)2 = a2 + b2 + 2ab]
By using the result 3 + 4i = (2 + i)2, we get
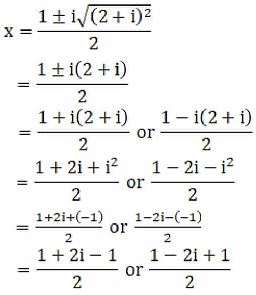
x = 2i/2 or (2 – 2i)/2
x = i or 2(1-i)/2
x = i or (1 – i)
∴ The roots of the given equation are (1-i), i
(ix) ix2 – x + 12i = 0
Given: ix2 – x + 12i = 0
ix2 + x(–1) + 12i = 0 [We know, i2 = –1]
So by substituting –1 = i2 in the above equation, we get
ix2 + xi2 + 12i = 0
i(x2 + ix + 12) = 0
x2 + ix + 12 = 0
x2 + ix – 12(–1) = 0
x2 + ix – 12i2 = 0 [Since, i2 = –1]
x2 – 3ix + 4ix – 12i2 = 0
x(x – 3i) + 4i(x – 3i) = 0
(x – 3i) (x + 4i) = 0
x – 3i = 0 or x + 4i = 0
x = 3i or –4i
∴ The roots of the given equation are -4i, 3i
(x) x2 – (3√2 – 2i)x – √2i = 0
Given: x2 – (3√2 – 2i)x – √2i = 0
We shall apply the discriminant rule.
Where, x = (-b ±√(b2 – 4ac))/2a
Here, a = 1, b = -(3√2 – 2i), c = –√2i
So,
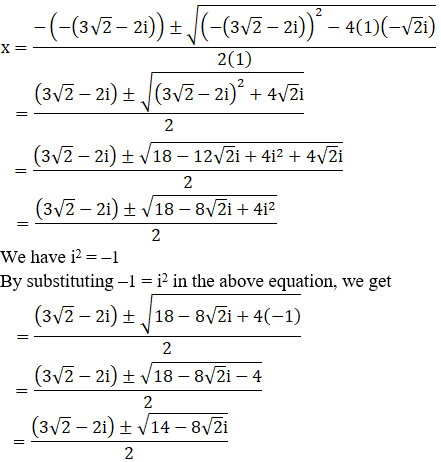

(xi) x2 – (√2 + i)x + √2i = 0
Given: x2 – (√2 + i)x + √2i = 0
x2 – (√2x + ix) + √2i = 0
x2 – √2x – ix + √2i = 0
x(x – √2) – i(x – √2) = 0
(x – √2) (x – i) = 0
(x – √2) = 0 or (x – i) = 0
x = √2 or x = i
∴ The roots of the given equation are i, √2
(xii) 2x2 – (3 + 7i)x + (9i – 3) = 0
Given: 2x2 – (3 + 7i)x + (9i – 3) = 0
We shall apply the discriminant rule.
Where, x = (-b ±√(b2 – 4ac))/2a
Here, a = 2, b = -(3 + 7i), c = (9i – 3)
So,
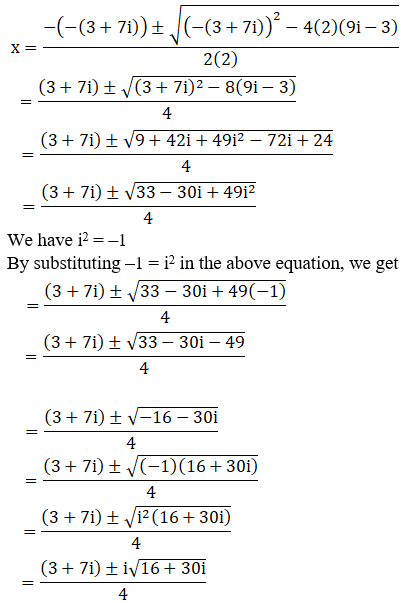
We can write 16 + 30i = 25 – 9 + 30i
16 + 30i = 25 + 9(–1) + 30i
= 25 + 9i2 + 30i [∵ i2 = –1]
= 52 + (3i)2 + 2(5)(3i)
= (5 + 3i)2 [∵ (a + b)2 = a2 + b2 + 2ab]
By using the result 16 + 30i = (5 + 3i)2, we get
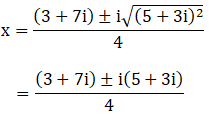
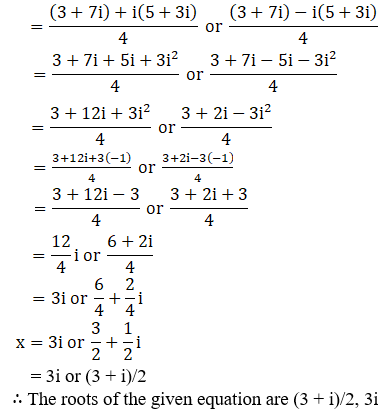
Also, access exercises of RD Sharma Solutions for Class 11 Maths Chapter 14 – Quadratic Equations
Frequently Asked Questions on RD Sharma Solutions for Class 11 Maths Chapter 14
What are the ways to learn the topics from RD Sharma Solutions for Class 11 Maths Chapter 14 quickly?
How should I prepare for the final exam using the RD Sharma Solutions for Class 11 Maths Chapter 14?
Can RD Sharma Solutions for Class 11 Maths Chapter 14 really help students with their board exam preparations?
Are RD Sharma Solutions for Class 11 Maths Chapter 14 helpful in effective exam preparation?
RD Sharma Solutions for Class 11 Maths Chapter 14 provide answers for each question of the textbook in simple language to help students score high marks in exams. The detailed answers designed by expert faculty provide various methods of solving complex problems in an efficient manner. Practising these solutions on a daily basis help students to analyse their areas of weakness and work on them for a better score.
Where can I access accurate answers of RD Sharma Solutions for Class 11 Maths Chapter 14?
Students can access accurate answers of RD Sharma Solutions for Class 11 Maths Chapter 14 at BYJU’S website. RD Sharma Solutions, prepared by BYJU’S experts, are the best study materials that provide students with numerous practice questions to answer. The solutions are designed with utmost care to help students grasp the concepts more effectively and score good marks in exams.




















Comments