Exercise 14.2 of Chapter 14 discusses problems based on quadratic equations with complex coefficients. Our team of expert faculty has prepared the solutions to help students in their exam preparation to obtain good marks in Maths. If you wish to secure an excellent score, then solving RD Sharma Class 11 Solutions is an utmost necessity. Practising the textbook questions will help you in analysing your level of preparation and build a strong command over the subject. Students can easily download the PDF from the links given below.
RD Sharma Solutions for Class 11 Maths Exercise 14.2 Chapter 14 – Quadratic Equations
Also, access another exercise of RD Sharma Solutions for Class 11 Maths Chapter 14 – Quadratic Equations
Access answers to RD Sharma Solutions for Class 11 Maths Exercise 14.2 Chapter 14 – Quadratic Equations
1. Solving the following quadratic equations by factorisation method:
(i) x2 + 10ix – 21 = 0
(ii) x2 + (1 – 2i)x – 2i = 0
(iii) x2 – (2√3 + 3i) x + 6√3i = 0
(iv) 6x2 – 17ix – 12 = 0
Solution:
(i) x2 + 10ix – 21 = 0
Given: x2 + 10ix – 21 = 0
x2 + 10ix – 21 × 1 = 0
We know, i2 = –1 ⇒ 1 = –i2
By substituting 1 = –i2 in the above equation, we get
x2 + 10ix – 21(–i2) = 0
x2 + 10ix + 21i2 = 0
x2 + 3ix + 7ix + 21i2 = 0
x(x + 3i) + 7i(x + 3i) = 0
(x + 3i) (x + 7i) = 0
x + 3i = 0 or x + 7i = 0
x = –3i or –7i
∴ The roots of the given equation are –3i, –7i
(ii) x2 + (1 – 2i)x – 2i = 0
Given: x2 + (1 – 2i)x – 2i = 0
x2 + x – 2ix – 2i = 0
x(x + 1) – 2i(x + 1) = 0
(x + 1) (x – 2i) = 0
x + 1 = 0 or x – 2i = 0
x = –1 or 2i
∴ The roots of the given equation are –1, 2i
(iii) x2 – (2√3 + 3i) x + 6√3i = 0
Given: x2 – (2√3 + 3i) x + 6√3i = 0
x2 – (2√3x + 3ix) + 6√3i = 0
x2 – 2√3x – 3ix + 6√3i = 0
x(x – 2√3) – 3i(x – 2√3) = 0
(x – 2√3) (x – 3i) = 0
(x – 2√3) = 0 or (x – 3i) = 0
x = 2√3 or x = 3i
∴ The roots of the given equation are 2√3, 3i
(iv) 6x2 – 17ix – 12 = 0
Given: 6x2 – 17ix – 12 = 0
6x2 – 17ix – 12 × 1 = 0
We know, i2 = –1 ⇒ 1 = –i2
By substituting 1 = –i2 in the above equation, we get
6x2 – 17ix – 12(–i2) = 0
6x2 – 17ix + 12i2 = 0
6x2 – 9ix – 8ix + 12i2 = 0
3x(2x – 3i) – 4i(2x – 3i) = 0
(2x – 3i) (3x – 4i) = 0
2x – 3i = 0 or 3x – 4i = 0
2x = 3i or 3x = 4i
x = 3i/2 or x = 4i/3
∴ The roots of the given equation are 3i/2, 4i/3
2. Solve the following quadratic equations:
(i) x2 – (3√2 + 2i) x + 6√2i = 0
(ii) x2 – (5 – i) x + (18 + i) = 0
(iii) (2 + i)x2 – (5- i)x + 2 (1 – i) = 0
(iv) x2 – (2 + i)x – (1 – 7i) = 0
(v) ix2 – 4x – 4i = 0
(vi) x2 + 4ix – 4 = 0
(vii) 2x2 + √15ix – i = 0
(viii) x2 – x + (1 + i) = 0
(ix) ix2 – x + 12i = 0
(x) x2 – (3√2 – 2i)x – √2i = 0
(xi) x2 – (√2 + i)x + √2i = 0
(xii) 2x2 – (3 + 7i)x + (9i – 3) = 0
Solution:
(i) x2 – (3√2 + 2i) x + 6√2i = 0
Given: x2 – (3√2 + 2i) x + 6√2i = 0
x2 – (3√2x + 2ix) + 6√2i = 0
x2 – 3√2x – 2ix + 6√2i = 0
x(x – 3√2) – 2i(x – 3√2) = 0
(x – 3√2) (x – 2i) = 0
(x – 3√2) = 0 or (x – 2i) = 0
x = 3√2 or x = 2i
∴ The roots of the given equation are 3√2, 2i
(ii) x2 – (5 – i) x + (18 + i) = 0
Given: x2 – (5 – i) x + (18 + i) = 0
We shall apply the discriminant rule,
Where, x = (-b ±√(b2 – 4ac))/2a
Here, a = 1, b = -(5-i), c = (18+i)
So,
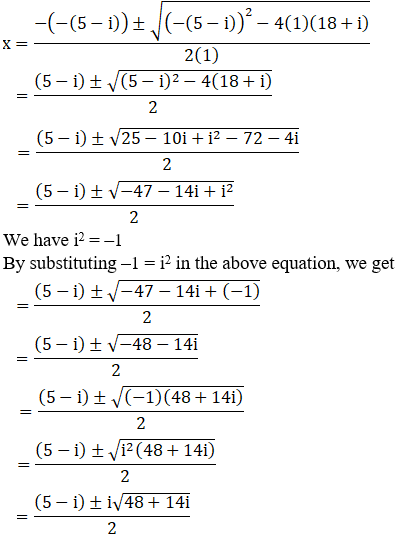
We can write 48 + 14i = 49 – 1 + 14i
So,
48 + 14i = 49 + i2 + 14i [∵ i2 = –1]
= 72 + i2 + 2(7)(i)
= (7 + i)2 [Since, (a + b)2 = a2 + b2 + 2ab]
By using the result 48 + 14i = (7 + i) 2, we get
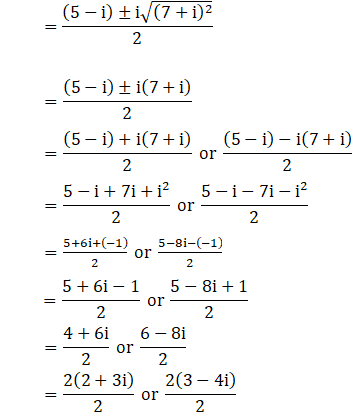
x = 2 + 3i or 3 – 4i
∴ The roots of the given equation are 3 – 4i, 2 + 3i
(iii) (2 + i)x2 – (5- i)x + 2 (1 – i) = 0
Given: (2 + i)x2 – (5- i)x + 2 (1 – i) = 0
We shall apply the discriminant rule,
Where, x = (-b ±√(b2 – 4ac))/2a
Here, a = (2+i), b = -(5-i), c = 2(1-i)
So,
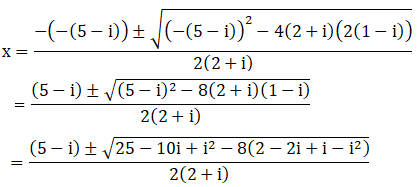
We have i2 = –1
By substituting –1 = i2 in the above equation, we get
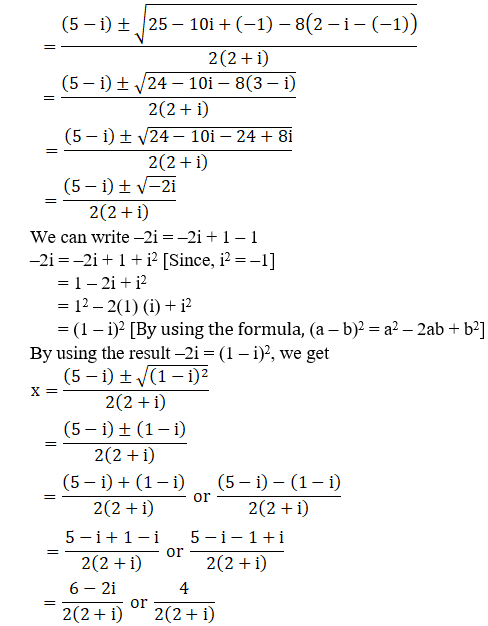
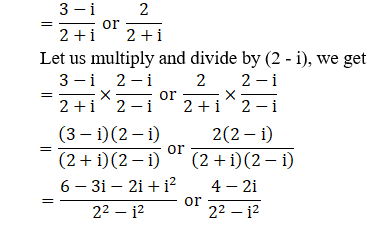
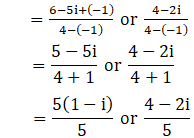
x = (1 – i) or 4/5 – 2i/5
∴ The roots of the given equation are (1 – i), 4/5 – 2i/5
(iv) x2 – (2 + i)x – (1 – 7i) = 0
Given: x2 – (2 + i)x – (1 – 7i) = 0
We shall apply the discriminant rule,
Where, x = (-b ±√(b2 – 4ac))/2a
Here, a = 1, b = -(2+i), c = -(1-7i)
So,
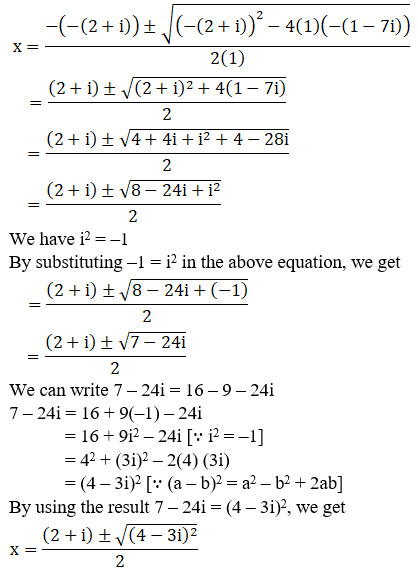
We can write 7 – 24i = 16 – 9 – 24i
7 – 24i = 16 + 9(–1) – 24i
= 16 + 9i2 – 24i [∵ i2 = –1]
= 42 + (3i)2 – 2(4) (3i)
= (4 – 3i)2 [∵ (a – b)2 = a2 – b2 + 2ab]
By using the result 7 – 24i = (4 – 3i)2, we get
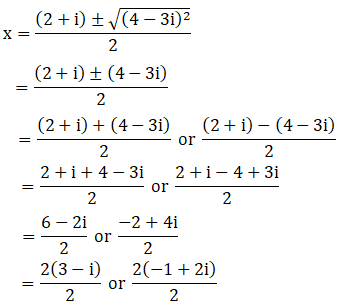
x = 3 – i or -1 + 2i
∴ The roots of the given equation are (-1 + 2i), (3 – i)
(v) ix2 – 4x – 4i = 0
Given: ix2 – 4x – 4i = 0
ix2 + 4x(–1) – 4i = 0 [We know, i2 = –1]
So by substituting –1 = i2 in the above equation, we get
ix2 + 4xi2 – 4i = 0
i(x2 + 4ix – 4) = 0
x2 + 4ix – 4 = 0
x2 + 4ix + 4(–1) = 0
x2 + 4ix + 4i2 = 0 [Since, i2 = –1]
x2 + 2ix + 2ix + 4i2 = 0
x(x + 2i) + 2i(x + 2i) = 0
(x + 2i) (x + 2i) = 0
(x + 2i)2 = 0
x + 2i = 0
x = –2i, -2i
∴ The roots of the given equation are –2i, –2i
(vi) x2 + 4ix – 4 = 0
Given: x2 + 4ix – 4 = 0
x2 + 4ix + 4(–1) = 0 [We know, i2 = –1]
So by substituting –1 = i2 in the above equation, we get
x2 + 4ix + 4i2 = 0
x2 + 2ix + 2ix + 4i2 = 0
x(x + 2i) + 2i(x + 2i) = 0
(x + 2i) (x + 2i) = 0
(x + 2i)2 = 0
x + 2i = 0
x = –2i, -2i
∴ The roots of the given equation are –2i, –2i
(vii) 2x2 + √15ix – i = 0
Given: 2x2 + √15ix – i = 0
We shall apply the discriminant rule,
Where, x = (-b ±√(b2 – 4ac))/2a
Here, a = 2, b = √15i, c = -i
So,
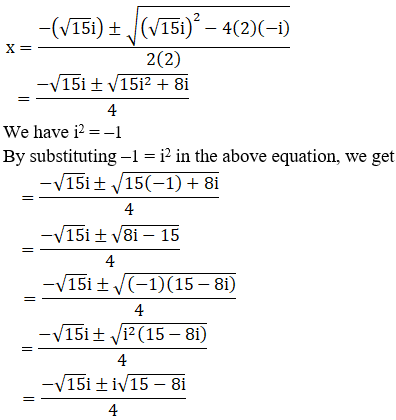
We can write 15 – 8i = 16 – 1 – 8i
15 – 8i = 16 + (–1) – 8i
= 16 + i2 – 8i [∵ i2 = –1]
= 42 + (i)2 – 2(4)(i)
= (4 – i)2 [Since, (a – b)2 = a2 – b2 + 2ab]
By using the result 15 – 8i = (4 – i)2, we get
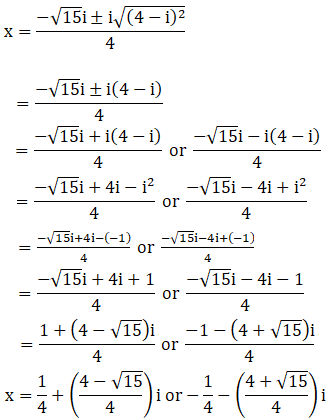
∴ The roots of the given equation are [1+ (4 – √15)i/4] , [-1 -(4 + √15)i/4]
(viii) x2 – x + (1 + i) = 0
Given: x2 – x + (1 + i) = 0
We shall apply the discriminant rule,
Where, x = (-b ±√(b2 – 4ac))/2a
Here, a = 1, b = -1, c = (1+i)
So,
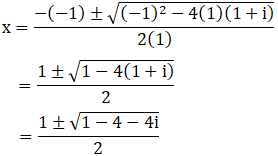
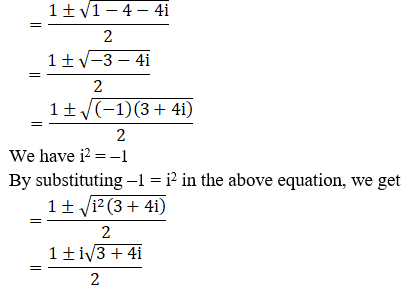
We can write 3 + 4i = 4 – 1 + 4i
3 + 4i = 4 + i2 + 4i [∵ i2 = –1]
= 22 + i2 + 2(2) (i)
= (2 + i)2 [Since, (a + b)2 = a2 + b2 + 2ab]
By using the result 3 + 4i = (2 + i)2, we get
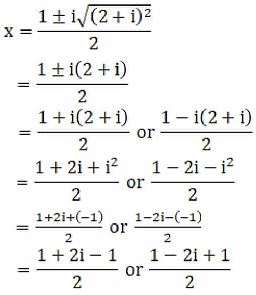
x = 2i/2 or (2 – 2i)/2
x = i or 2(1-i)/2
x = i or (1 – i)
∴ The roots of the given equation are (1-i), i
(ix) ix2 – x + 12i = 0
Given: ix2 – x + 12i = 0
ix2 + x(–1) + 12i = 0 [We know, i2 = –1]
so by substituting –1 = i2 in the above equation, we get
ix2 + xi2 + 12i = 0
i(x2 + ix + 12) = 0
x2 + ix + 12 = 0
x2 + ix – 12(–1) = 0
x2 + ix – 12i2 = 0 [Since, i2 = –1]
x2 – 3ix + 4ix – 12i2 = 0
x(x – 3i) + 4i(x – 3i) = 0
(x – 3i) (x + 4i) = 0
x – 3i = 0 or x + 4i = 0
x = 3i or –4i
∴ The roots of the given equation are -4i, 3i
(x) x2 – (3√2 – 2i)x – √2i = 0
Given: x2 – (3√2 – 2i)x – √2i = 0
We shall apply the discriminant rule,
Where, x = (-b ±√(b2 – 4ac))/2a
Here, a = 1, b = -(3√2 – 2i), c = –√2i
So,
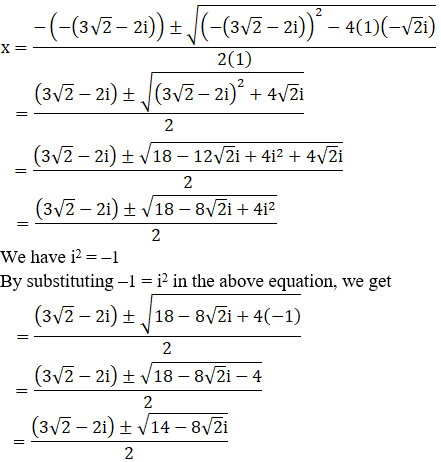

(xi) x2 – (√2 + i)x + √2i = 0
Given: x2 – (√2 + i)x + √2i = 0
x2 – (√2x + ix) + √2i = 0
x2 – √2x – ix + √2i = 0
x(x – √2) – i(x – √2) = 0
(x – √2) (x – i) = 0
(x – √2) = 0 or (x – i) = 0
x = √2 or x = i
∴ The roots of the given equation are i, √2
(xii) 2x2 – (3 + 7i)x + (9i – 3) = 0
Given: 2x2 – (3 + 7i)x + (9i – 3) = 0
We shall apply the discriminant rule,
Where, x = (-b ±√(b2 – 4ac))/2a
Here, a = 2, b = -(3 + 7i), c = (9i – 3)
So,
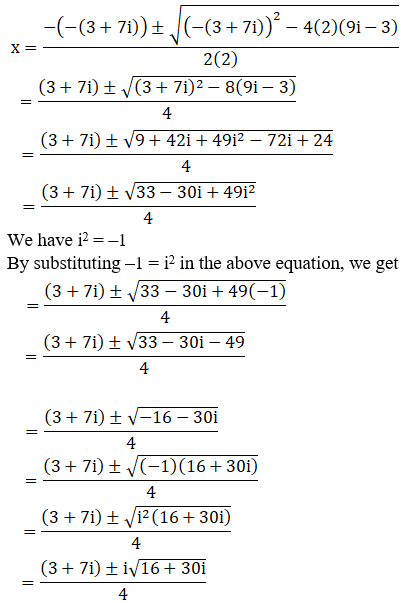
We can write 16 + 30i = 25 – 9 + 30i
16 + 30i = 25 + 9(–1) + 30i
= 25 + 9i2 + 30i [∵ i2 = –1]
= 52 + (3i)2 + 2(5)(3i)
= (5 + 3i)2 [∵ (a + b)2 = a2 + b2 + 2ab]
By using the result 16 + 30i = (5 + 3i)2, we get
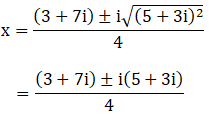
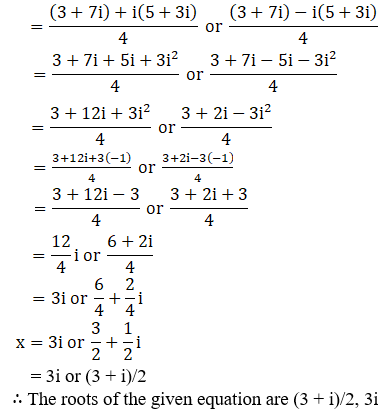














Comments