Exercise 6.2 of Chapter 6 discusses problems based on the graph of a cosine function. The exercise problems are solved by our experienced faculty, having in-depth knowledge of these concepts. In addition, the solutions are designed as per the weightage allotted in the board exam. While solving problems, students can use the solutions PDF for quick reference and guidance, which helps in scoring good marks in their exams. RD Sharma Class 11 Solutions are available in PDF format, which can be downloaded easily from the links given below.
RD Sharma Solutions for Class 11 Maths Exercise 6.2 Chapter 6 – Graphs of Trigonometric Functions
Also, access other exercises of RD Sharma Solutions for Class 11 Maths Chapter 6 – Graphs of Trigonometric Functions
Access answers to RD Sharma Solutions for Class 11 Maths Exercise 6.2 Chapter 6 – Graphs of Trigonometric Functions
1. Sketch the graphs of the following trigonometric functions:
(i) f (x) = cos (x – π/4)
(ii) g (x) = cos (x + π/4)
(iii) h (x) = cos2 2x
(iv) ϕ (x) = 2 cos (x – π/6)
(v) ψ (x) = cos (3x)
(vi) u (x) = cos2 x/2
(vii) f (x) = cos πx
(viii) g (x) = cos 2π x
Solution:
(i) f (x) = cos (x – π/4)
We know that g (x) = cos x is a periodic function with period 2π.
So, f (x) = cos (x – π/4) is a periodic function with period π. So, we will draw the graph of f (x) = cos (x – π/4) in the interval [0, π]. The values of f (x) = cos (x – π/4) at various points in [0, π] are listed in the following table:
| x | 0 (A) | π/4 (B) | π/2 (C) | 3π/4 (D) | π (E) | 5π/4 (F) | 3π/2 (G) | 7π/4 (H) |
| f (x) = cos (x – π/4) | 1/√2 = 0.7 | 1 | 1/√2 = 0.7 | 0 | -1/√2 = -0.7 | -1 | -1/√2 = -0.7 | 0 |
The required curve is:

(ii) g (x) = cos (x + π/4)
We know that f (x) = cos x is a periodic function with period 2π.
So, g (x) = cos (x + π/4) is a periodic function with period π. So, we will draw the graph of g (x) = cos (x + π/4) in the interval [0, π]. The values of g (x) = cos (x + π/4) at various points in [0, π] are listed in the following table:
| x | 0 (A) | π/4 (B) | π/2 (C) | 3π/4 (D) | π (E) | 5π/4 (F) | 3π/2 (G) | 7π/4 (H) |
| g (x) = cos (x + π/4) | 1/√2 = 0.7 | 0 | -1/√2 = -0.7 | -1 | -1/√2 = -0.7 | 0 | 1/√2 = 0.7 | 1 |
The required curve is:

(iii) h (x) = cos2 2x
We know that f (x) = cos x is a periodic function with period 2π.
So, h (x) = cos2 2x is a periodic function with period π. So, we will draw the graph of h (x) = cos2 2x in the interval [0, π]. The values of h (x) = cos2 2x at various points in [0, π] are listed in the following table:
| x | 0 (A) | π/4 (B) | π/2 (C) | 3π/4 (D) | π (E) | 5π/4 (F) | 3π/2 (G) |
| h (x) = cos2 2x | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
The required curve is:

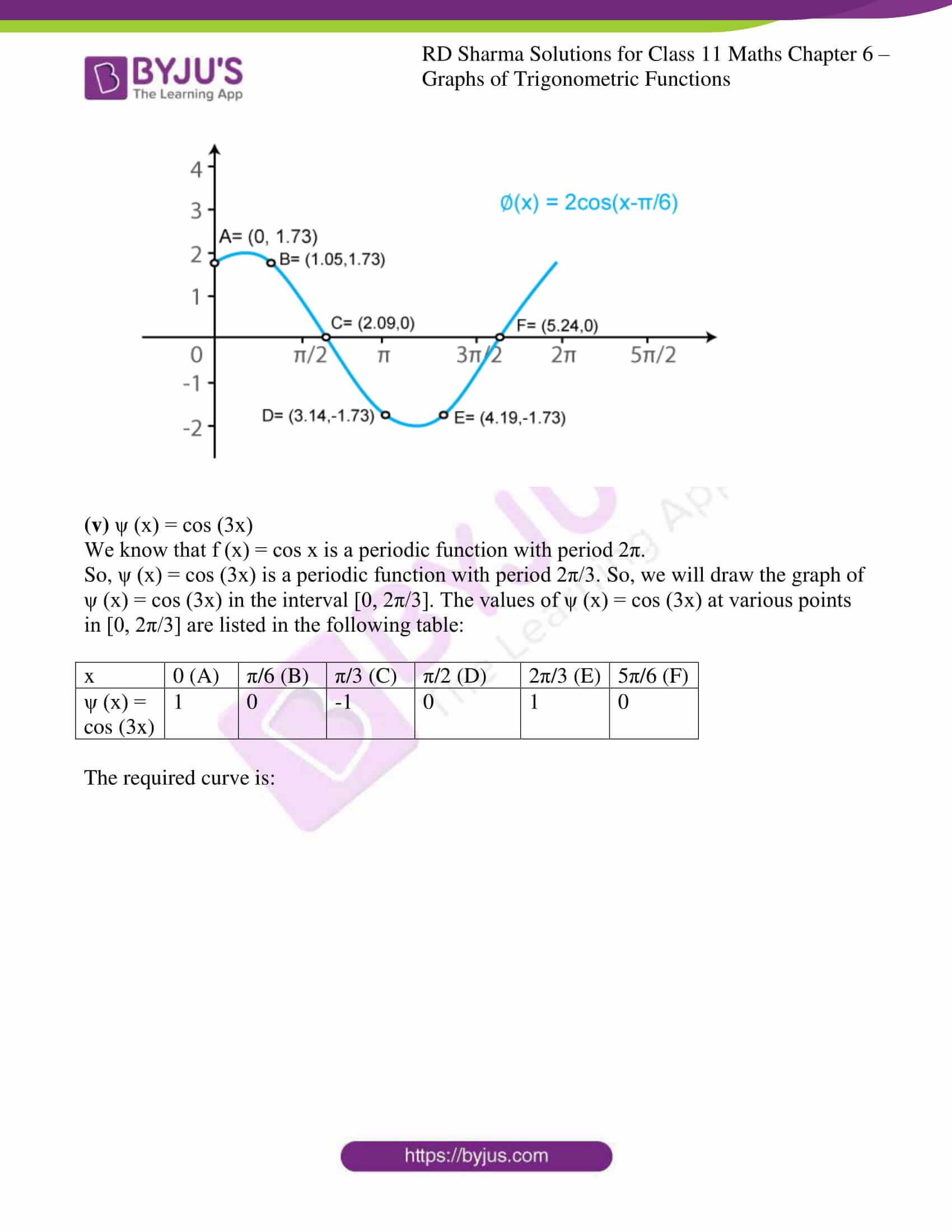
(iv) ϕ (x) = 2 cos (x – π/6)
We know that f (x) = cos x is a periodic function with period 2π.
So, ϕ (x) = 2cos (x – π/6) is a periodic function with period π. So, we will draw the graph of ϕ (x) = 2cos (x – π/6) in the interval [0, π]. The values of ϕ (x) = 2cos (x – π/6) at various points in [0, π] are listed in the following table:
| x | 0 (A) | π/3 (B) | 2π/3 (C) | π (D) | 4π/3 (E) | 5π/3 (F) |
| ϕ (x) = 2 cos (x – π/6) | √3 = 1.73 | √3 = 1.73 | 0 | -√3 = -1.73 | -√3 = -1.73 | 0 |
The required curve is:

(v) ψ (x) = cos (3x)
We know that f (x) = cos x is a periodic function with period 2π.
So, ψ (x) = cos (3x) is a periodic function with period 2π/3. So, we will draw the graph of ψ (x) = cos (3x) in the interval [0, 2π/3]. The values of ψ (x) = cos (3x) at various points in [0, 2π/3] are listed in the following table:
| x | 0 (A) | π/6 (B) | π/3 (C) | π/2 (D) | 2π/3 (E) | 5π/6 (F) |
| ψ (x) = cos (3x) | 1 | 0 | -1 | 0 | 1 | 0 |
The required curve is:

(vi) u (x) = cos2 x/2
We know that f (x) = cos x is a periodic function with period 2π.
So, u (x) = cos2 (x/2) is a periodic function with period π. So, we will draw the graph of u (x) = cos2 (x/2) in the interval [0, π]. The values of u (x) = cos2 (x/2) at various points in [0, π] are listed in the following table:
| x | 0 (A) | π (B) | 2π (C) | 3π (D) |
| u (x) = cos2 x/2 | 1 | 0 | 1 | 0 |
The required curve is:

(vii) f (x) = cos πx
We know that g (x) = cos x is a periodic function with period 2π.
So, f (x) = cos (πx) is a periodic function with period 2. So, we will draw the graph of f (x) = cos (πx) in the interval [0, 2]. The values of f (x) = cos (πx) at various points in [0, 2] are listed in the following table:
| x | 0 (A) | 1/2 (B) | 1 (C) | 3/2 (D) | 2 (E) | 5/2 (F) |
| f (x) = cos πx | 1 | 0 | -1 | 0 | 1 | 0 |
The required curve is:

(viii) g (x) = cos 2π x
We know that f (x) = cos x is a periodic function with period 2π.
So, g (x) = cos (2πx) is a periodic function with period 1. So, we will draw the graph of g (x) = cos (2πx) in the interval [0, 1]. The values of g (x) = cos (2πx) at various points in [0, 1] are listed in the following table:
| x | 0 (A) | 1/4 (B) | 1/2 (C) | 3/4 (D) | 1 (E) | 5/4 (F) | 3/2 (G) | 7/4 (H) | 2 |
| g (x) = cos 2π x | 1 | 0 | -1 | 0 | 1 | 0 | -1 | 0 | 1 |
The required curve is:

2. Sketch the graphs of the following curves on the same scale and the same axes:
(i) y = cos x and y = cos (x – π/4)
(ii) y = cos 2x and y = cos (x – π/4)
(iii) y = cos x and y = cos x/2
(iv) y = cos2 x and y = cos x
Solution:
(i) y = cos x and y = cos (x – π/4)
We know that the functions y = cos x and y = cos (x – π/4) are periodic functions with periods π and π.
The values of these functions are tabulated below:
| x | 0 | π/4 | π/2 | 3π/4 | π | 5π/4 | 3π/2 | 7π/4 |
| y = cos x | 1 | 1/√2 = 0.7 | 0 | -1/√2 = -0.7 | -1 | -1/√2 = -0.7 | 0 | 1 |
| y = cos (x – π/4) | 1/√2 = 0.7 | 1 | 1/√2 = 0.7 | 0 | -1/√2 = -0.7 | -1 | -1/√2 = -0.7 | 0 |
The required curve is:

(ii) y = cos 2x and y = cos 2(x – π/4)
We know that the functions y = cos 2x and y = cos 2(x – π/4) are periodic functions with periods π and π.
The values of these functions are tabulated below:
| x | 0 | π/4 | π/2 | 3π/4 | π | 5π/4 | 3π/2 | 7π/4 |
| y = cos x | 1 | 0 | -1 | 0 | 1 | 0 | -1 | 0 |
| y = cos 2 (x – π/4) | 0 | 1 | 0 | -1 | 0 | 1 | 0 | -1 |
The required curve is:

(iii) y = cos x and y = cos x/2
We know that the functions y = cos x and y = cos (x/2) are periodic functions with periods π and π.
The values of these functions are tabulated below:
| x | 0 | π/2 | π | 3π/2 | 2π |
| y = cos x | 1 | 0 | -1 | 0 | 1 |
| y = cos x/2 | 1 | 1/√2 = 0.7 | 0 | -1/√2 = -0.7 | -1 |
The required curve is:

(iv) y = cos2 x and y = cos x
We know that the functions y = cos2 x and y = cos x are periodic functions with period 2π.
The values of these functions are tabulated below:
| x | 0 | π/2 | π | 3π/2 | 2π |
| y = cos2 x | 1 | 0 | 1 | 0 | 1 |
| y = cos x | 1 | 0 | -1 | 0 | 1 |
The required curve is:










Comments