RD Sharma Solutions Class 6 Chapter 17 Exercise 17.4
Exercise 17.4
1. The total number of lines of symmetry of a scalene triangle is
Soln: (d) none of these
This is because the line of symmetry of a scalene triangle is 0.
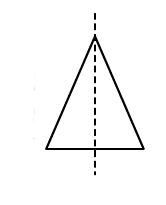
2. The total number of lines of symmetry of an isosceles triangle is
Soln: (a) 1
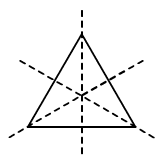
3. An equilateral triangle is symmetrical about each of its
Soln: (d) all the above
In equilateral triangle altitudes, angle bisectors and medians are all the same.
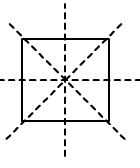
4. The total number of lines of symmetry of a square is
Soln: (d) 4
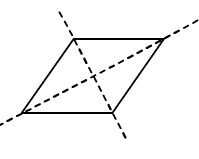
5. A rhombus is symmetrical about
Soln: (a) Each of its diagonals
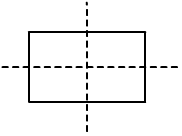
6. The number of lines of symmetry of a rectangle is
Soln: (b) 2
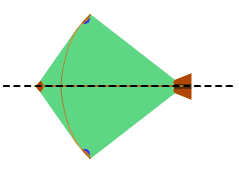
7. The number of lines of symmetry of a kite is
Soln: (b) 1
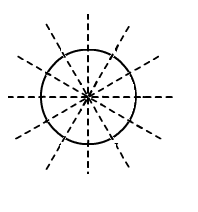
8. The number of lines of symmetry of a circle is
Soln: (d) Unlimited
A circle has an infinite number of symmetry all along the diameters. It has an infinite number of diameters
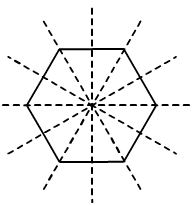
9. The number of lines of symmetry of a regular hexagon is
Soln: (c) 6
10. The number of lines of symmetry of an n – sided regular polygon is
Soln: (a) n
The number of lines of symmetry of a regular polygon is equal to the sides of the polygon. If it has ‘n’ number of sides, then there are ‘n’ lines of symmetry
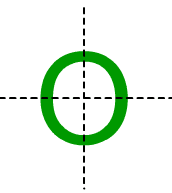
11. The number of lines of symmetry of the letter O of the English alphabet is
Soln: (c) 2
12. The number of lines of symmetry of the letter Z of the English alphabet is
Soln: (a) 0
Z has no line of symmetry
Comments