The first thing which comes to our mind when we think about plane figures is boundaries and their regions. In this chapter, we learn about the concept of area and perimeter of plane figures. These two concepts are of great importance in our daily lives as they help to determine measurements.
The problems in this chapter are based on shapes like closed and open curves, rectangle, square, equilateral triangle, etc. These concepts are explained in simple language based on the understanding capacity of students to make it easy for them during exam preparation. RD Sharma Solutions for Class 6 Chapter 20 Mensuration PDF is provided here.
RD Sharma Solutions for Class 6 Maths Chapter 20: Mensuration
Access answers to Maths RD Sharma Solutions for Class 6 Chapter 20: Mensuration
Exercise 20.1 page: 20.5
1. Which of the following are closed curves? Which of them are simple?
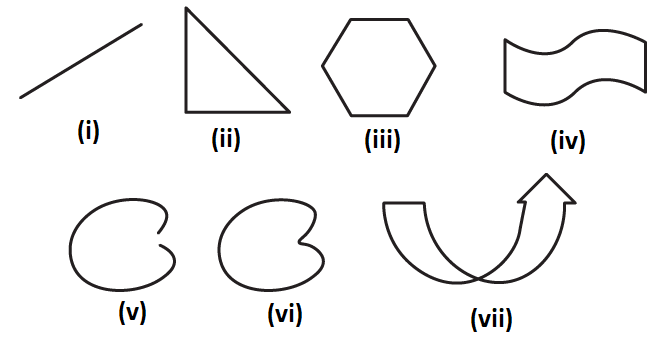
Solution:
The figures (ii), (iii), (iv), (vi) and (vii) are closed curves and the figures (ii), (iii), (iv) and (vi) are simple closed curves.
2. Define perimeter of a closed figure.
Solution:
The length of the boundary of a closed figure is known as its perimeter.
3. Find the perimeter of each of the following shapes:
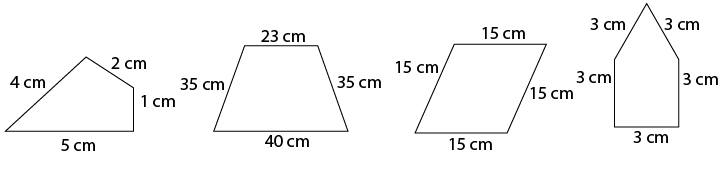
Solution:
We know that perimeter is the sum of lengths of all the sides of a closed figure.
(i) Perimeter of the given figure = 4 + 2 + 1 + 5 = 12 cm
(ii) Perimeter of the given figure = 23 + 35 + 40 + 35 = 133 cm
(iii) Perimeter of the given figure = 15 + 15 + 15 + 15 = 60 cm
(iv) Perimeter of the given figure = 3 + 3 + 3 + 3 + 3 = 15 cm
Exercise 20.2 page: 20.10
1. Find the perimeters of the rectangles whose lengths and breadths are given below:
(i) 7 cm, 5 cm
(ii) 5 cm, 4 cm
(iii) 7.5 cm, 4.5 cm
Solution:
(i) We know that the perimeter of a rectangle = 2 (L + B)
It is given that L = 7 cm and B = 5 cm
So the perimeter of a rectangle = 2 (7 + 5) = 2 × 12 = 24 cm
(ii) We know that the perimeter of a rectangle = 2 (L + B)
It is given that L = 5 cm and B = 4 cm
So the perimeter of a rectangle = 2 (5 + 4) = 2 × 9 = 18 cm
(iii) We know that the perimeter of a rectangle = 2 (L + B)
It is given that L = 7.5 cm and B = 4.5 cm
So the perimeter of a rectangle = 2 (7.5 + 4.5) = 2 × 12 = 24 cm
2. Find the perimeters of the squares whose sides are given below:
(i) 10 cm
(ii) 5 m
(iii) 115.5 cm
Solution:
(i) We know that the perimeter of a square = 4 × Length of one side
It is given that L = 10 cm
So the perimeter of a square = 4 × 10 = 40 cm
(ii) We know that the perimeter of a square = 4 × Length of one side
It is given that L = 5 m
So the perimeter of a square = 4 × 5 = 20 m
(iii) We know that the perimeter of a square = 4 × Length of one side
It is given that L = 115.5 cm
So the perimeter of a square = 4 × 115.5 = 462 cm
3. Find the side of the square whose perimeter is:
(i) 16 m
(ii) 40 cm
(iii) 22 cm
Solution:
(i) We know that side of a square = perimeter/ 4
It is given that perimeter = 16 m
So the side of the square = 16/4 = 4 m
(ii) We know that side of a square = perimeter/ 4
It is given that perimeter = 40 cm
So the side of the square = 40/4 = 10 cm
(iii) We know that side of a square = perimeter/ 4
It is given that perimeter = 22 cm
So the side of the square = 22/4 = 5.5 cm
4. Find the breadth of the rectangle whose perimeter is 360 cm and whose length is
(i) 116 cm
(ii) 140 cm
(iii) 102 cm
Solution:
We know that the perimeter of a rectangle = 2 (L + B)
So the breadth of the rectangle = perimeter/2 – length
(i) It is given that perimeter = 360 cm and length = 116 cm
So the breadth of the rectangle = 360/2 – 116 = 180 – 116 = 64 cm
(ii) It is given that perimeter = 360 cm and length = 140 cm
So the breadth of the rectangle = 360/2 – 140 = 180 – 140 = 40 cm
(iii) It is given that perimeter = 360 cm and length = 102 cm
So the breadth of the rectangle = 360/2 – 102 = 180 – 102 = 78 cm
5. A rectangular piece of lawn is 55 m wide and 98 m long. Find the length of the fence around it.
Solution:
The dimensions of lawn are
Breadth = 55 m
Length = 98 m
We know that
Perimeter of lawn = 2 (L + B)
By substituting the values
Perimeter of lawn = 2 (98 +55)
So we get
Perimeter of lawn = 2 × 153 = 306 m
Hence, the length of the fence around the lawn is 306 m.
6. The side of a square field is 65 m. What is the length of the fence required all around it?
Solution:
It is given that
Side of a square field = 65 m
So the perimeter of square field = 4 × side of the square
By substituting the values
Perimeter of square field = 4 × 65 = 260 m
Hence, the length of the fence required all around the square field is 260 m.
7. Two sides of a triangle are 15 cm and 20 cm. The perimeter of the triangle is 50 cm. What is the third side?
Solution:
It is given that
First side of triangle = 15 cm
Second side of triangle = 20 cm
In order to find the length of third side
We know that perimeter of a triangle is the sum of all three sides of a triangle
So the length of third side = perimeter of triangle – sum of length of other two sides
By substituting the values
Length of third side = 50 – (15 + 20) = 15 cm.
Hence, the length of third side is 15 cm.
8. A wire of length 20 m is to be folded in the form of a rectangle. How many rectangles can be formed by folding the wire if the sides are positive integers in metres?
Solution:
Given:
Length of wire 20 m is folded in the form of rectangle
So the perimeter = 20 m
It can be written as
2 (L + B) = 20 m
On further calculation
L + B = 10 m
If the sides are positive integers in metres the possible dimensions are (1m, 9m), (2m, 8m), (3m, 7m), (4m, 6m) and (5m, 5m)
Hence, five rectangles can be formed using the given wire.
9. A square piece of land has each side equal to 100 m. If 3 layers of metal wire has to be used to fence it, what is the length of the wire needed?
Solution:
It is given that
Each side of a square field = 100 m
We can find the wire required to fence the square field by determining the perimeter = 4 × each side of a square field
By substituting the values
Perimeter of the square field = 4 × 100 = 400 m
So the length of wire which is required to fence three layers is = 3 × 400 = 1200 m
Hence, the length of wire needed to fence 3 layers is 1200 m.
10. Shikha runs around a square of side 75 m. Priya runs around a rectangle with length 60 m and breadth 45 m. Who covers the smaller distance?
Solution:
It is given that
Shikha runs around a square of side = 75 m
So the perimeter = 4 × 75 = 300 m
Priya runs around a rectangle having
Length = 60 m
Breadth = 45 m
So the distance covered can be found from the perimeter = 2 (L + B)
By substituting the values
Perimeter = 2 (60 + 45) = 2 × 105 = 210 m
Hence, Priya covers the smaller distance of 210 m.
11. The dimensions of a photographs are 30 cm × 20 cm. What length of wooden frame is needed to frame the picture?
Solution:
It is given that
Dimensions of a photographs = 30 cm × 20 cm
So the required length of the wooden frame can be determined from the perimeter of the photograph = 2 (L + B)
By substituting the values = 2 (30 + 20) = 2 × 50 = 100 cm
Hence, the length of the wooden frame required to frame the picture is 100 cm.
12. The length of a rectangular field is 100 m. If the perimeter is 300 m, what is its breadth?
Solution:
The dimensions of rectangular field are
Length = 100 m
Perimeter = 300 m
We know that perimeter = 2 (L + B)
It can be written as
Breadth = perimeter/2 – length
By substituting the values
Breadth = (300-200)/2 = 100/2 = 50 m
Hence, the breadth of the rectangular field is 50 m.
13. To fix fence wires in a garden, 70 m long and 50 m wide, Arvind bought metal pipes for posts. He fixed a post every 5 metres apart. Each post was 2 m long. What is the total length of the pipes he bought for the posts?
Solution:
The dimensions of garden are
Length = 70 m
Breadth = 50 m
So the perimeter = 2 (L + B)
By substituting the values
Perimeter = 2 (70 + 50) = 2 × 120 = 240 m
Given:
Arvind fixes a post every 5 metres apart
No. of posts required = 240/5 = 48
The length of each post = 2 m
So the total length of the pipe required = 48 × 2 = 96 m
Hence, the total length of the pipes he bought for the posts is 96 m.
14. Find the cost of fencing a rectangular park of length 175 m and breadth 125 m at the rate of Rs 12 per meter.
Solution:
The dimensions of the rectangular park are
Length = 175 m
Breadth = 125 m
So the perimeter = 2 (L + B)
By substituting the values
Perimeter = 2 (175 + 125) = 2 × 300 = 600 m
It is given that the cost of fencing = Rs 12 per meter
So the total cost of fencing = 12 × 600 = Rs 7200
Hence, the cost of fencing a rectangular park is Rs 7200.
15. The perimeter of a regular pentagon is 100 cm. How long is each side?
Solution:
We know that a regular pentagon is a closed polygon having 5 sides of same length.
It is given that
Perimeter of a regular pentagon = 100 cm
It can be written as
Perimeter = 5 × side of the regular pentagon
So we get
Side of the regular pentagon = Perimeter/5
By substituting the values
Side of the regular pentagon = 100/5 = 20 cm
Hence, the side of the regular pentagon measures 20 cm.
16. Find the perimeter of a regular hexagon with each side measuring 8 m.
Solution:
We know that a regular hexagon is a closed polygon which has six sides of same length.
It is given that
Side of the regular hexagon = 8 m
So we get
Perimeter = 6 × side of the regular hexagon
By substituting the values
Perimeter = 6 × 8 = 48 m
Hence, the perimeter of a regular hexagon is 48 m.
17. A rectangular piece of land measure 0.7 km by 0.5 km. Each side is to be fenced with four rows of wires. What length of the wire is needed?
Solution:
It is given that
Measure of rectangular piece of land = 0.7 km × 0.5 km
We know that
Perimeter = 2 (L + B)
By substituting the values
Perimeter = 2 (0.7 + 0.5) = 2 × 1.2 = 2.4 km
The above obtained perimeter = one row of wire needed to fence the rectangular piece of land
So the length of wire needed to fence the land with 4 rows of wire = 4 × 2.4 = 9.6 km
Hence, the length of wire needed is 9.6 km.
18. Avneet buys 9 square paving slabs, each with a side of ½ m. He lays them in the form of a square.
(i) What is the perimeter of his arrangement?
(ii) Shari does not like his arrangement. She gets him to lay them out like a cross. What is the perimeter of her arrangement?
(iii) Which has greater perimeter?
(iv) Avneet wonders, if there is a way of getting an even greater perimeter. Can you find a way of doing this? (The paving slabs must meet along complete edges they cannot be broken)

Solution:
(i) It is given that length of each side of the slab = ½ m
One side of the square is formed by three slabs in a square arrangement
Length of side = 3 × ½ = 3/2 m
So the perimeter of the square arrangement = 4 × 3/2 = 6 m
(ii) From the figure, cross arrangement has 8 sides which form periphery of the arrangement and measure 1 m each.
It also has 4 sides which measure ½ m each
Perimeter of the cross arrangement = 1 + ½ + 1 + 1 + ½ + 1 + 1 + ½ + 1 + 1 + ½ + 1 = 8 + 2 = 10 m

(iii) We know that
Perimeter of cross arrangement = 10 m
Perimeter of square arrangement = 6 m
Hence, the perimeter of cross arrangement is greater than the perimeter of square arrangement.
(iv) No, Avneet cannot arrange the slabs having perimeter more than 10 m.
Exercise 20.3 page: 20.14
1. The following figures are drawn on a squared paper. Count the number of squares enclosed by each figure and find its area, taking the area of each square as 1 cm2. (Fig. 20.25).

Solution:
(i) The given shape has 16 complete squares.
It is given that area of one square = 1 cm2
So the area of the given shape = 16 × 1 = 16 cm2
(ii) The given shape has 36 complete squares.
It is given that area of one square = 1 cm2
So the area of the given shape = 36 × 1 = 36 cm2
(iii) The given shape has 15 complete and 6 half squares.
It is given that area of one square = 1 cm2
So the area of the given shape = 15 + 6 × 12 = 18 cm2
(iv) The given shape has 20 complete and 8 half squares.
It is given that area of one square = 1 cm2
So the area of the given shape = 20 + 8 × 12 = 24 cm2
(v) The given shape has 13 complete, 8 more than half and 7 less than half squares.
It is given that area of one square = 1 cm2
So the area of the given shape = 13 + 8 × 1 = 21 cm2
(vi) The given shape has 8 complete, 6 more than half and 4 less than half squares.
It is given that area of one square = 1 cm2
So the area of the given shape = 8 + 6 × 1 = 14 cm2
2. On a squared paper, draw (i) a rectangle, (ii) a triangle (iii) any irregular closed figure. Find the approximate area of each by counting the number of squares complete, more than half and exactly half.
Solution:
(i) A rectangle
The given shape has 18 complete squares
Assume that area of one square = 1 cm2
So the area of the rectangle = 18 × 1 = 18 cm2

(ii) A triangle
The given shape has 4 complete, 6 more than half and 6 less than half squares.
Assume that area of one square = 1 cm2
So the area of the square = 4 + 6 × 1 = 10 cm2

(iii) Any irregular figure
The given shape has 10 complete, 1 exactly half, 7 more than half and 6 less than half squares.
Assume that area of one square = 1 cm2
So the area of the shape = 10 + 1 × 12 + 7 × 1 = 17.5 cm2

3. Draw any circle on the graph paper. Count the squares and use them to estimate the area of the circular region.
Solution:

The given circles has 21 complete, 15 more than half and 8 less than half squares.
Assume that area of one square = 1 cm2
By neglecting less than half squares, we get
Area of the circle = 21 + 15 = 36 cm2
4. Use tracing paper and centimetre graph paper to compare the areas of the following pairs of figures:

Solution:

With the help of tracing paper trace both the figures on a graph
Figure (i) has 4 complete, 9 more than half and 9 less than half squares.
Assume that area of one square = 1 cm2
By neglecting less than half squares, we get
Area of the shape = 4 + 9 = 13 cm2
Figure (ii) has 8 complete, 11 more than half and 10 less than half squares.
Assume that area of one square = 1 cm2
By neglecting less than half squares, we get
Area of the shape = 8 + 11 = 19 cm2
By comparing the areas of both the shapes, we know that the figure (ii) has area greater than that of figure (i).
Exercise 20.4 page: 20.21
1. Find the area of a rectangle, whose
(i) Length = 6 cm, breadth = 3 cm
(ii) Length = 8 cm, breadth = 3 cm
(iii) Length = 4.5 cm, breadth = 2 cm.
Solution:
(i) We know that area of a rectangle = L × B
It is given that Length = 6 cm, breadth = 3 cm
By substituting the values
Area of a rectangle = 6 × 3 = 18 cm2
(ii) We know that area of a rectangle = L × B
It is given that Length = 8 cm, breadth = 3 cm
By substituting the values
Area of a rectangle = 8 × 3 = 24 cm2
(iii) We know that area of a rectangle = L × B
It is given that Length = 4.5 cm, breadth = 2 cm
By substituting the values
Area of a rectangle = 4.5 × 2 = 9 cm2
2. Find the area of a square whose side is:
(i) 5 cm
(ii) 4.1 cm
(iii) 5.5 cm
(iv) 2.6 cm
Solution:
(i) We know that area of a square = side × side
It is given that side of a square = 5 cm
So the area of the square = 5 × 5 = 25 cm2
(ii) We know that area of a square = side × side
It is given that side of a square = 4.1 cm
So the area of the square = 4.1 × 4.1 = 16.81 cm2
(iii) We know that area of a square = side × side
It is given that side of a square = 5.5 cm
So the area of the square = 5.5 × 5.5 = 30.25 cm2
(iv) We know that area of a square = side × side
It is given that side of a square = 2.6 cm
So the area of the square = 2.6 × 2.6 = 6.76 cm2
3. The area of a rectangle is 49 cm2 and its breadth is 2.8 cm. Find the length of the rectangle.
Solution:
It is given that area of a rectangle = 49 cm2
Breadth of a rectangle = 2.8 cm
We know that
Area of a rectangle = L × B
It can be written as
L = Area/B = 49/2.8 = 17.5 cm
Hence, the length of the rectangle is 17.5 cm.
4. The side of a square is 70 cm. Find its area and perimeter.
Solution:
It is given that side of a square = 70 cm
We know that area of a square = side × side
By substituting the values
Area of a square = 70 × 70 = 4900 cm2
We know that perimeter of a square = 4 × side
By substituting the values
Perimeter of a square = 4 × 70 = 280 cm
Hence, the area of square is 4900 cm2 and the perimeter of square is 280 cm.
5. The area of a rectangle is 225 cm2 and its one side is 25 cm, find its other side.
Solution:
It is given that
Area of a rectangle = 225 cm2
Length of one side = 25 cm
We know that area of a rectangle = Product of length of two sides
So the other side = area/side
By substituting the values
Other side = 225/25 = 9 cm
Hence, the other side of the rectangle is 9 cm.
6. What will happen to the area of rectangle if its
(i) Length and breadth are trebled
(ii) Length is doubled and breadth is same
(iii) Length is doubled and breadth is halved.
Solution:
(i) Length and breadth are trebled
Consider l as the initial length and b as the initial breadth
So the original area = l × b
If the length and breadth are trebled it becomes three times more than the original value
New length = 3l
New breadth = 3b
New area of the rectangle = 3l × 3b = 9lb
Hence, the area of the rectangle becomes 9 times more than its original area.
(ii) Length is doubled and breadth is same
Consider l as the initial length and b as the initial breadth
So the original area = l × b
If the length is doubled and breadth is same we get
New length = 2l
New breadth = b
New area of the rectangle = 2l × b = 2lb
Hence, the area of the rectangle becomes 2 times more than the original area.
(iii) Length is doubled and breadth is halved
Consider l as the initial length and b as the initial breadth
So the original area = l × b
If the length is doubled and breadth is halved we get
New length = 2l
New breadth = b/2
New area of the rectangle = 2l × b/2 = lb
Hence, the area of the rectangle does not change.
7. What will happen to the area of a square if its side is:
(i) Tripled
(ii) Increased by half of it.
Solution:
(i) Tripled
Consider s as the original side of the square
We know that original area = s × s = s2
If the side of the square is tripled we get
New side = 3s
So the new area of the square = 3s × 3s = 9s2
Hence, the area becomes 9 times more than that of the original area.
(ii) Increased by half of it
Consider s as the original side of the square
We know that original area = s × s = s2
If the side of the square is increased by half of it we get
New side = s + s/2 = 3s/2
So the new area of the square = 3s/2 × 3s/2 = 9s2/4
Hence, the area becomes 9/4 times more than that of the original area.
8. Find the perimeter of a rectangle whose area is 500 cm2 and breadth is 20 cm.
Solution:
It is given that
Area of the rectangle = 500 cm2
Breadth of the rectangle = 20 cm
We know that area = L × B
It can be written as
L = Area/B
By substituting the values
L = 500/20 = 25 cm
We know that perimeter = 2 (L + B)
By substituting the values
Perimeter = 2 (25 + 20) = 2 × 45 = 90 cm
Hence, the perimeter of the rectangle is 90 cm.
9. A rectangle has the area equal to that of a square of side 80 cm. If the breadth of the rectangle is 20 cm, find its length.
Solution:
It is given that
Side of a square = 80 cm
So the area of the square = side × side
By substituting the values
Area of square = 80 × 80 = 6400 cm2
We know that area of rectangle = area of square = 6400 cm2
Breadth = 20 cm
Area of rectangle = L × B
It can be written as
L = Area/B = 6400/20 = 320 cm
Hence, the length of the rectangle is 320 cm.
10. Area of a rectangle of breadth 17 cm is 340 cm2. Find the perimeter of the rectangle.
Solution:
The dimensions of rectangle are
Breadth = 17 cm
Area = 340 cm2
We know that
Area of rectangle = L × B
It can be written as
L = Area/B = 340/17 = 20 cm
So the perimeter = 2 (L + B)
By substituting the values
Perimeter = 2 (20 + 17) = 2 × 37 = 74 cm
Hence, the perimeter of the rectangle is 74 cm.
11. A marble tile measures 15 cm × 20 cm. How many tiles will be required to cover a wall of size 4 m × 6 m?
Solution:
Measure of marble tile = 15 cm × 20 cm
Size of wall = 4 m × 6 m = 400 cm × 600 cm
So we get area of tile = 15 cm × 20 cm = 300 cm2
Area of wall = 400 cm × 600 cm = 240000 cm2
No. of tiles required to cover the wall = Area of wall/ Area of one tile
Substituting the values
No. of tiles required to cover the wall = 240000/300 = 800 tiles
Hence, 800 tiles are required to cover a wall of size 4 m × 6 m.
12. A marble tile measures 10 cm × 12 cm. How many tiles will be required to cover a wall of size 3 m × 4 m? Also, find the total cost of the tiles at the rate of Rs 2 per tile.
Solution:
Measure of marble tile = 10 cm × 12 cm
Size of the wall = 3 m × 4 m = 300 cm × 400 cm
So the area of marble tile = 10 cm × 12 cm = 120 cm2
Area of wall = 300 cm × 400 cm = 120000 cm2
No. of tiles required to cover the wall = Area of wall/ Area of one tile
Substituting the values
No. of tiles required to cover the wall = 120000/120 = 1000 tiles
It is given that
Cost of one tile = Rs 2
So the cost of 1000 tiles = 1000 × 2 = Rs 2000
Hence, 1000 number of tiles are required to cover the wall and the cost is Rs 2000.
13. One side of a square plot is 250 m, find the cost of levelling it at the rate of Rs 2 per square metre.
Solution:
It is given that
Side of one tile of a square plot = 250 m
So the area = side × side = 250 × 250 = 62500 m2
Cost of levelling = Rs 2 per square meter
So the cost of levelling 62500 m2 = 62500 × 2 = Rs 125000
Hence, the cost of levelling is Rs 125000.
14. The following figures have been split into rectangles. Find their areas. (The measures are given in centimetres)

Solution:
(i) The given figure has two rectangles II and IV and two squares I and III.
So the area of square I = side × side = 3 × 3 = 9 cm2
The same way area of rectangle II = L × B = 2 × 1 = 2 cm2
Area of square III = side × side = 3 × 3 = 9 cm2
Similarly area of rectangle IV = L × B = 2 × 4 = 8 cm2
So the total area of the figure = Area of square I + Area of rectangle II + Area of square III + Area of rectangle IV
By substituting the values
Total area of the figure = 9 + 2 + 9 + 8 = 28 cm2

(ii) The given figure has three rectangles I, II and III.
So the area of rectangle I = L × B = 3 × 1 = 3 cm2
Area of rectangle II = L × B = 3 × 1 = 3 cm2
Area of rectangle III = L × B = 3 × 1 = 3 cm2
So the total area of the figure = Area of rectangle I + Area of rectangle II + Area of rectangle III
By substituting the values
Total area of the figure = 3 + 3 + 3 = 9 cm2

15. Split the following shapes into rectangles and find the area of each. (The measures are given in centimetres)

Solution:
(i) The given figure has two rectangles I and II.
So the area of rectangle I = L × B = 10 × 2 = 20 cm2
In the same way area of rectangle II = L × B = 10 × 3/2 = 15 cm2
So the total area of the figure = Area of rectangle I + Area of rectangle II
By substituting the values
Total area of the figure = 20 + 15 = 35 cm2

(ii) The given figure has two squares I and III and one rectangle II.
So the area of square I = Area of square III = side × side = 7 × 7 = 49 cm2
The area of rectangle II = 21 × 7 = 147 cm2
So the total area of the figure = Area of square I + Area of rectangle II + Area of square III
By substituting the values
Total area of the figure = 49 + 49 + 147 = 245 cm2

(iii) The given figure has two rectangles I and II.
So the area of rectangle I = L × B = 5 × 1 = 5 cm2
The same way, area of rectangle II = L × B = 4 × 1 = 4 cm2
So the total area of the figure = Area of rectangle I + Area of rectangle II
By substituting the values
Total area of the figure = 5 + 4 = 9 cm2

16. How many tiles with dimensions 5 cm and 12 cm will be needed to fit a region whose length and breadth are respectively:
(i) 100 cm and 144 cm
(ii) 70 cm and 36 cm
Solution:
(i) Tile dimensions = 5 cm × 12 cm
Region dimensions = 100 cm × 144 cm
So the area of tile = 5 cm × 12 cm = 60 cm2
Similarly area of region = 100 cm × 144 cm = 14400 cm2
No. of tiles which is required to cover the region = Area of region/ Area of one tile
By substituting the values
No. of tiles which is required to cover the region = 14400/60 = 240 tiles
(ii) Tile dimensions = 5 cm × 12 cm
Region dimensions = 70 cm × 36 cm
So the area of tile = 5 cm × 12 cm = 60 cm2
Similarly area of region = 70 cm × 36 cm = 2520 cm2
No. of tiles which is required to cover the region = Area of region/ Area of one tile
By substituting the values
No. of tiles which is required to cover the region = 2520/60 = 42 tiles
Objective Type Questions page: 20.23
Mark the correct alternative in each of the following:
1. The sides of a rectangle are in the ratio 5: 4. If its perimeter is 72 cm, then its length is
(a) 40 cm
(b) 20 cm
(c) 30 cm
(d) 60 cm
Solution:
The option (b) is the correct answer.
Consider the sides of the rectangle as 5x and 4x.
We know that, perimeter of rectangle = 2 (Length + Breadth)
By substituting the values
72 = 2 (5x + 4x)
On further calculation
72 = 2 × 9x
So we get
72 = 18x
By division
x = 72/18 = 4
Hence, the length of the rectangle = 5x = 5 × 4 = 20 cm
2. The cost of fencing a rectangular field 34 m long and 18 m wide at Rs 2.25 per meter is
(a) Rs 243
(b) Rs 234
(c) Rs 240
(d) Rs 334
Solution:
The option (b) is the correct answer.
We must find the perimeter of the rectangle for fencing the field.
The dimensions of the rectangle are
Length = 34m
Breadth = 18m
We know that Perimeter = 2 (Length + Breadth)
By substituting the values
Perimeter of the rectangle = 2 (34 + 18) = 2 × 52 = 104 m
So the cost of fencing the field at the rate of Rs. 2.25 per meter = 104 × 2.25 = Rs. 234
3. If the cost of fencing a rectangular field at Rs. 7.50 per meter is Rs. 600, and the length of the field is 24 m, then the breadth of the field is
(a) 8 m
(b) 18 m
(c) 24 m
(d) 16 m
Solution:
The option (d) is the correct answer.
It is given that cost of fencing the rectangular field = Rs. 600
So the rate of fencing the field = Rs. 7.50 per m
We know that perimeter of the field = Cost of fencing/Rate of fencing
By substituting the values
Perimeter of the field = 600/7.50 = 80 m
Length of the field = 24 m
So we get breadth of the field = Perimeter/2- Length = 80/2- 24 = 16 m
4. The cost of putting a fence around a square field at Rs 2.50 per meter is Rs 200. The length of each side of the field is
(a) 80 m
(b) 40 m
(c) 20 m
(d) None of these
Solution:
The option (c) is the correct answer.
It is given that cost of fencing the square field = Rs. 200
So the rate of fencing the field = Rs. 2.50
We know that, perimeter of the square field = Cost of fencing/Rate of fencing
By substituting the values
Perimeter of the square field = 200/2.50 = 80 m
Perimeter of square = 4 × Side of the square
It can be written as
Side of the square = Perimeter/4 = 80/4 = 20 m
5. The length of a rectangle is three times of its width. If the length of the diagonal is 8√10 m, then the perimeter of the rectangle is
(a) 15√10 m
(b) 16√10 m
(c) 24√10 m
(d) 64 m
Solution:
The option (d) is the correct answer.
Consider ABCD as a rectangle.
Assume that the width of the rectangle BC = x m
We know that the length is three times width of the rectangle.
So, length of the rectangle AB = 3x m

AC is the diagonal of rectangle
Consider ABC as a right angled triangle.
AC2 = AB2 + BC2
By substituting the values
640 = 9x2 + x2
We get
640 = 10x2
On further calculation
x2 = 640/10 = 64
x = √64 = 8 m
So the breadth of the rectangle x = 8 m
Length of the rectangle 3x = 3 × 8 = 24 m
Perimeter = 2 (Length + Breadth)
By substituting the values
Perimeter = 2 (24 + 8) = 2 × 32 = 64 m
6. If a diagonal of a rectangle is thrice its smaller side, then its length and breadth are in the ratio
(a) 3: 1
(b) √3: 1
(c) √2 : 1
(d) 2√2: 1
Solution:
The option (d) is the correct answer.
Assume that the length of the smaller side of the rectangle BC = x
Length of the larger side AB = y
It is given that the length of the diagonal is three times that of the smaller side.

Diagonal of the rectangle 3x = AC
By using Pythagoras theorem
(AC) 2 = (AB) 2 + (BC) 2
By substituting the values
(3x) 2 = (x) 2 + (y) 2
On further calculation
9x2 = x2 + y2
We get
8x2 = y2
By taking square roots of both sides,
2√2 x = y
Hence, the ratio of the larger side to the smaller side is 2√2: 1.
7. The ratio of the areas of two squares, one having its diagonal double than the other, is
(a) 1: 2
(b) 2: 3
(c) 3: 1
(d) 4: 1
Solution:
The option (d) is the correct answer.
Consider ABCD and PQRS as the two squares. We know that, the diagonal of square PQRS is twice the diagonal of square ABCD.

PR = 2 AC
Area of the square = Diagonal2/2
Area of PQRS = PR2/2
In the same way, area of ABCD = AC2/2
From the question, we know that:
If AC = x units, we get PR = 2x units
Area of PQRS/Area of ABCD = (PR2×2)/ (2×AC2)
By substituting the value
Area of PQRS/Area of ABCD = [(2x) 2×2]/ [2×x2] = 4/1
Hence, the ratio of the areas of squares PQRS and ABCD is 4: 1.
8. If the ratio of areas of two squares is 225 : 256, then the ratio of their perimeters is
(a) 225 : 256
(b) 256 : 225
(c) 15 : 16
(d) 16 : 15
Solution:
The option (c) is the correct answer.
Consider ABCD and PQRS as the two squares.
Let the lengths of each side of ABCD and PQRS be x and y.
We know that
Area of sq. ABCD/Area of sq. PQRS = x2/y2
So we get x2/y2= 225/256
By taking square roots on both sides,
x/y = 15/16
By taking the ratio of their perimeters, we get
Perimeter of sq. ABCD/Primeter of sq. PQRS = (4 × side of sq. ABCD)/ (4 × side of sq. PQRS) = 4x/4y
By removing common terms in numerator and denominator
Perimeter of sq. ABCD/Perimeter of sq. PQRS = x/ y
So perimeter of sq. ABCD/Perimeter of sq. PQRS = 15/16
Hence, the ratio of their perimeters = 15: 16
9. If the sides of a square are halved, then its area
(a) remains same
(b) becomes half
(c) becomes one fourth
(d) becomes double
Solution:
The option (c) is the correct answer.
Consider x as the side of the square.
We know that area of a square = Side × Side = x × x = x2
If the sides are halved, we get new side = x/2
So the new area = (x/2)2= x2/4
From this we know that the area has become one fourth of its previous value.
10. A rectangular carpet has area 120 m2 and perimeter 46 meters. The length of its diagonal is
(a) 15 m
(b) 16 m
(c) 17 m
(d) 20 m
Solution:
The option (c) is the correct answer.
It is given that area of the rectangle = 120 m2
Perimeter of the rectangle = 46 m
Consider l and b as the length and breadth.
Area of the rectangle = l × b = 120 m2
Perimeter of the rectangle = 2 (l + b) = 46
So we get
(l + b) = 46/2 = 23 m
Length of the diagonal of the rectangle = l2 + b2
It can be written as
(l2 + b2) = (l + b) 2 – 2 (l × b)
By substituting the values
(l2 + b2) = (23)2 – 2 (120) = 529 – 240 = 289
By adding square roots on both sides
Length of the diagonal of the rectangle = √l2 + b2 = √289 = 17 m
Hence, the length of the diagonal of the rectangle is 17m.
11. If the ratio between the length and the perimeter of a rectangular plot is 1: 3, then the ratio between the length and breadth of the plot is
(a) 1: 2
(b) 2: 1
(c) 3: 2
(d) 2: 3
Solution:
The option (b) is the correct answer.
Given that Length of rectangle/Perimeter of rectangle = 1/3
So we get
l/ (2l + 2b) = 1/3
By cross multiplication, we get:
3l = 2l + 2b
On further calculation
l = 2b
We get
l/ b= 2/1
Hence, the ratio of the length and the breadth is 2: 1.
12. If the length of the diagonal of a square is 20 cm, then its perimeter is
(a) 10√2cm
(b) 40 cm
(c) 40√2cm
(d) 200 cm
Solution:
The option (c) is the correct answer.
It is given that length of the diagonal = 20 cm
So the length of the side of a square = Length of Diagonal/√2 = 20/√2 = (2 × 10)/√2
We get
Length of the side of a square = (√2 × √2 × 10)/√2 = 10√2 cm
Hence, perimeter of the square = 4 × Side = 4 ×10√2 = 40√2 cm


























Comments