We see many structures, objects and figures, etc., which are evenly balanced and in pleasing proportions. Just by looking at them we get to know that they are symmetrical. Some live examples are Taj Mahal and India Gate, etc. These structures are beautiful because of their symmetry.
An object or a structure, when cutting into two halves, giving the same structure of equal length, is called symmetry. The line which passes through them is the line of symmetry. Students can download RD Sharma Solutions for Class 6 Chapter 17 Symmetry PDF from the links provided here.
RD Sharma Solutions for Class 6 Maths Chapter 17: Symmetry
Access answers to Maths RD Sharma Solutions for Class 6 Chapter 17: Symmetry
Exercise 17.1 page: 17.4
1. List any four symmetrical objects from your phone or school. Also, mention the line of symmetry.
Solution:
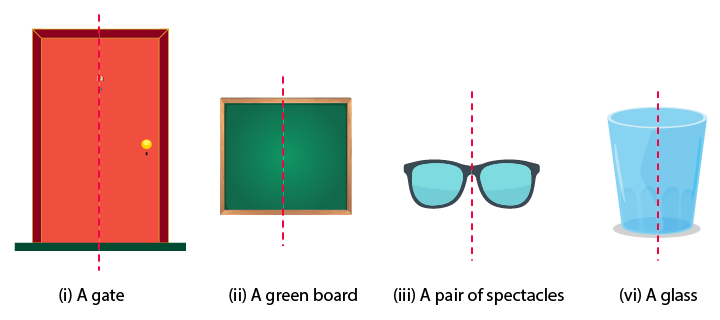
2. Identify the symmetrical instruments from your mathematical instrument box.
Solution:
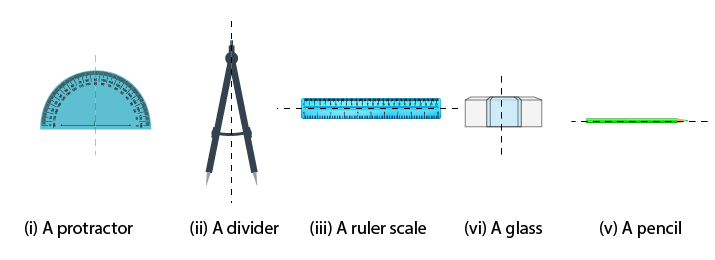
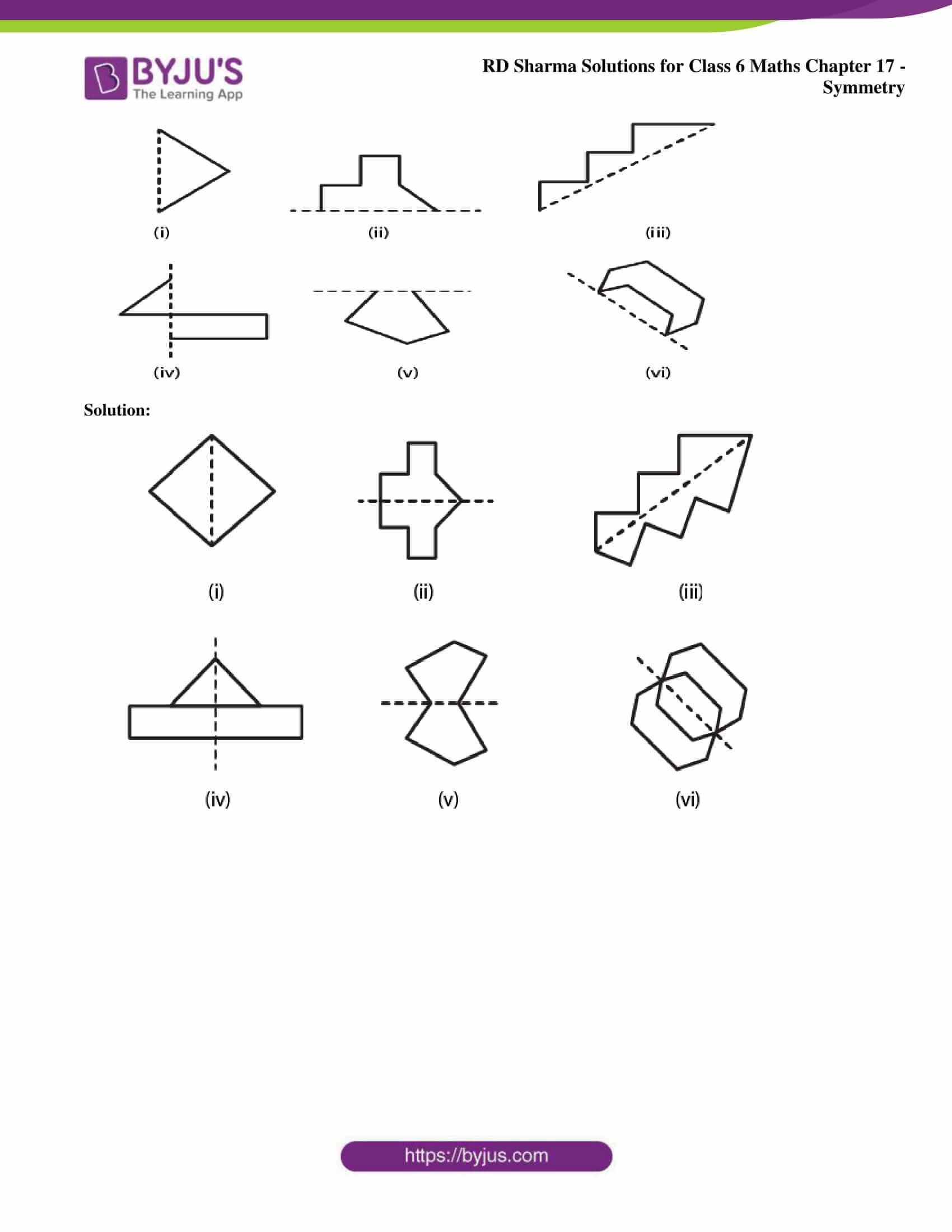
3. Copy each of the following on a squared paper and compute them in such a way that the dotted line is the line of symmetry.
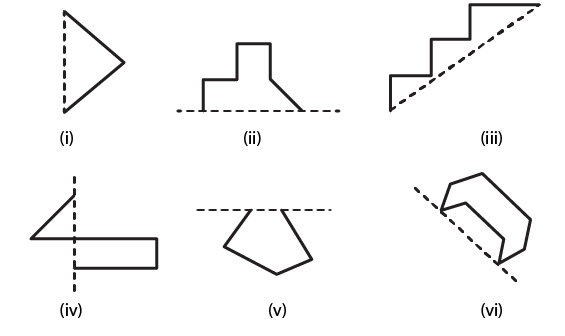
Solution:
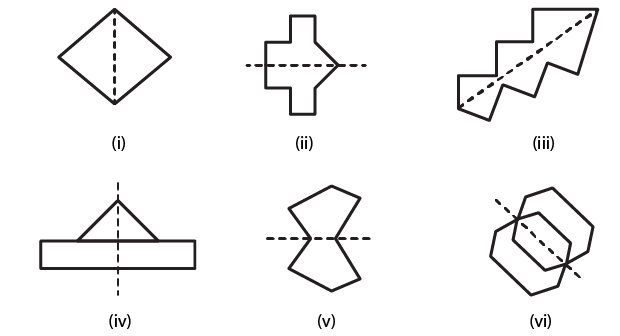
Exercise 17.2 page: 17.5
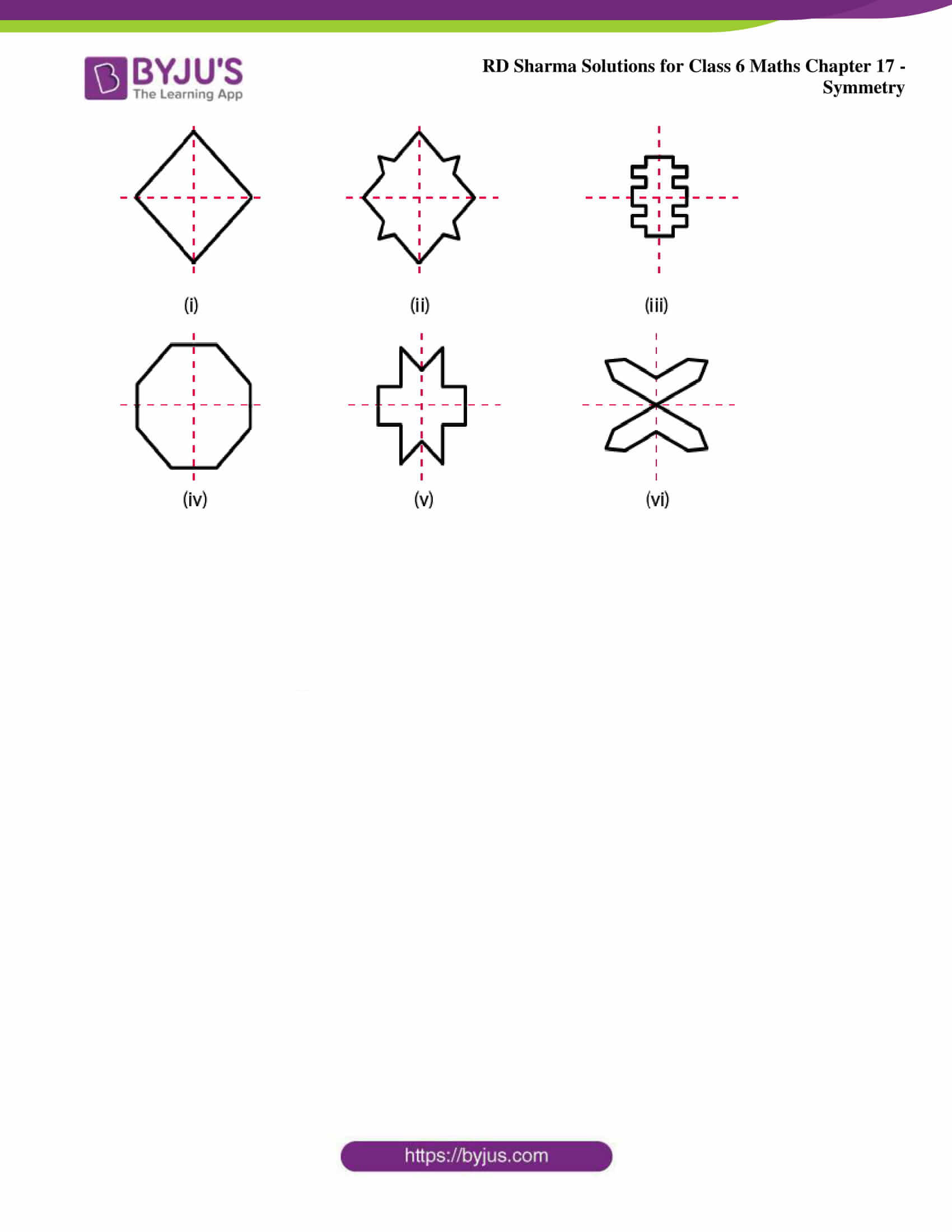
1. Find the number of lines of symmetry in each of the following shapes.
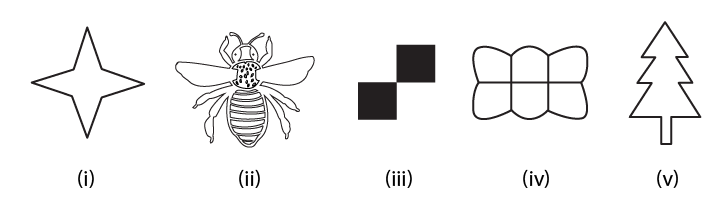
Solution:
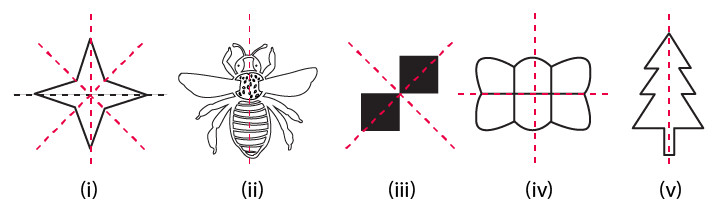
2. Copy the following drawings on squared paper and complete each one of them in such a way that resulting figure has two dotted lines as two lines of symmetry:
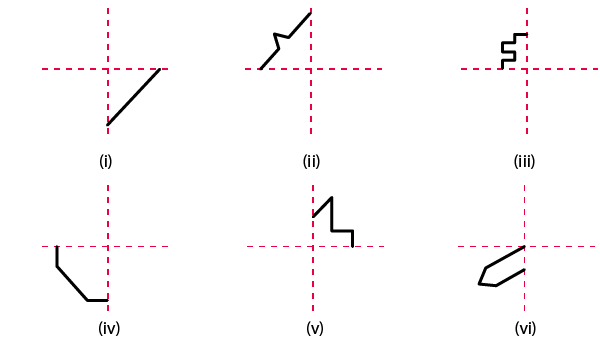
Solution:
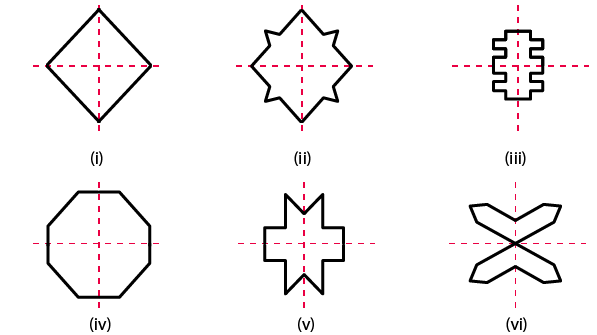
Exercise 17.3 page: 17.11
1. Complete the following table:

Solution:
| Shape | Rough Figure | Number of lines of symmetry |
| (i) Scalene triangle |  |
0 |
| (ii) Isosceles triangle |  |
1 |
| (iii) Equilateral triangle |  |
3 |
| (iv) Rectangle |  |
2 |
| (v) Square |  |
4 |
| (vi) Parallelogram |  |
0 |
| (vii) Rhombus |  |
2 |
| (viii) Line |  |
Infinitely many |
| (ix) Line Segment |  |
1 |
| (x) Angle |  |
1 |
| (xi) Isosceles trapezium |  |
1 |
| (xii) Kite |  |
1 |
| (xiii) Arrow-head |  |
1 |
| (xiv) Semi-circle |  |
1 |
| (xv) Circle |  |
Infinitely many |
| (xvi) Regular pentagon |  |
5 |
| (xvii) Regular hexagon |  |
6 |
2. Consider the English alphabets A to Z. List among them the letters which have
(i) vertical line of symmetry. (like A)
(ii) horizontal lines of symmetry. (like B)
(iii) vertical and horizontal lines of symmetry. (like I)
(iv) no line of symmetry. (like Q)
Solution:
(i) Vertical line of symmetry. (like A)

(ii) Horizontal lines of symmetry. (like B)

(iii) Vertical and horizontal lines of symmetry. (like I)

(iv) No line of symmetry. (like Q)

3. Can you draw a triangle having:
(i) exactly one line of symmetry
(ii) exactly two lines of symmetry.
(iii) three lines of symmetry.
(iv) no line of symmetry.
Solution:
(i) Exactly one line of symmetry.
Yes, an isosceles triangle.

(ii) Exactly two lines of symmetry.
No.
(iii) Three lines of symmetry.
Yes, an equilateral triangle.

(iv) No line of symmetry.
Yes, a scalene triangle.

4. On a squared paper, sketch the following:
(i) A triangle with a horizontal line of symmetry but no vertical line of symmetry.
(ii) A quadrilateral with both horizontal and vertical lines of symmetry.
(iii) A quadrilateral with a horizontal line of symmetry but no vertical line of symmetry.
(iv) A hexagon with exactly two lines of symmetry.
(v) A hexagon with six lines of symmetry.
Solution:

5. Draw neat diagrams solving the line (or lines) of symmetry and give the specific name to the quadrilateral having:
(i) only one line of symmetry. How many such quadrilaterals are there?
(ii) its diagonals as the only lines of symmetry.
(iii) two lines of symmetry other than diagonals.
(iv) more than two lines of symmetry.
Solution:
(i) Only one line of symmetry.

(ii) Diagonals as the only lines of symmetry.

(iii) Two lines of symmetry other than diagonals.

(iv) More than two lines of symmetry.

6. Write the specific names of all the three quadrilaterals which have only one line of symmetry.
Solution:

7. Trace each of the following figures and draw the lines of symmetry, if any:

Solution:

8. On squared paper copy the triangle in each of the following figures. In each case draw the line(s) of symmetry if any and identify the type of the triangle.

Solution:

(i) It is an isosceles triangle having only one line of symmetry.
(ii) It is an equilateral triangle having three lines of symmetry.
(iii) It is a right angled triangle having no line of symmetry.
(iv) It is an isosceles triangle having one line of symmetry.
9. Find the lines of symmetry for each of the following shapes:

Solution:

10. State whether the following statements are true or false:
(i) A right-angled triangle can have at most one line of symmetry.
(ii) An isosceles triangle with more than one line of symmetry must be an equilateral triangle.
(iii) A pentagon with one line of symmetry can be drawn.
(iv) A pentagon with more than one line of symmetry must be regular.
(v) A hexagon with line of symmetry can be drawn.
(vi) A hexagon with more than two lines of symmetry must be regular.
Solution:
(i) True

(ii) True

(iii) True

(iv) True

(v) True

(vi) True

Objective Type Questions page: 17.14
Mark the correct alternative in each of the following:
1. The total number of lines of symmetry of a scalene triangle is
(a) 1
(b) 2
(c) 3
(d) None of these
Solution:
The option (d) is the correct answer.
The total number of lines of symmetry of a scalene triangle is 0.
2. The total number of lines of symmetry of an isosceles triangle is
(a) 1
(b) 2
(c) 3
(d) None of these
Solution:
The option (a) is the correct answer.
The total number of lines of symmetry of an isosceles triangle is 1.

3. An equilateral triangle is symmetrical about each of its
(a) altitudes
(b) medians
(c) angle bisectors
(d) all the above
Solution:
The option (d) is the correct answer.
An equilateral triangle is symmetrical about each of its altitudes, angle bisectors and medians.

4. The total number of lines of symmetry of a square is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
The option (d) is the correct answer.
The total number of lines of symmetry of a square is 4.

5. A rhombus is symmetrical about
(a) each of its diagonals
(b) the line joining the mid-points of its opposite sides
(c) perpendicular bisectors of each of its sides
(d) none of these
Solution:
The option (a) is the correct answer.
A rhombus is symmetrical about each of its diagonals.

6. The number of lines of symmetry of a rectangle is
(a) 0
(b) 2
(c) 4
(d) 1
Solution:
The option (b) is the correct answer.
The number of lines of symmetry of a rectangle is 2.

7. The number of lines of symmetry of a kite is
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
The option (b) is the correct answer.
The number of lines of symmetry of a kite is 1.

8. The number of lines of symmetry of a circle is
(a) 0
(b) 1
(c) 4
(d) unlimited
Solution:
The option (d) is the correct answer.
The number of lines of symmetry of a circle is unlimited.

9. The number of lines of symmetry of a regular hexagon is
(a) 1
(b) 3
(c) 6
(d) 8
Solution:
The option (c) is the correct answer.
The number of lines of symmetry of a regular hexagon is 6.

10. The number of lines of symmetry of an n-sided regular polygon is
(a) n
(b) 2n
(c) n/2
(d) none of these
Solution:
The option (a) is the correct answer.
The number of lines of symmetry of an n-sided regular polygon is n.
11. The number of lines of symmetry of the letter O of the English alphabet is
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
The option (c) is the correct answer.
The number of lines of symmetry of the letter O of the English alphabet is 2.
12. The number of lines of symmetry of the letter Z of the English alphabet is
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
The option (a) is the correct answer.
The number of lines of symmetry of the letter Z of the English alphabet is 0.





















Comments