RD Sharma Solutions Class 6 Chapter 20 Exercise 20.5
Exercise 20.5
Mark the correct alternative in each of the following:
1. The sides of a rectangle are in the ratio 5 : 4. If its perimeter is 72 cm, then its length is
(a) 40 cm (b) 20 cm (c) 30 cm (d) 60 cm
Answer: (b) 20 cm
Explanation:
Let the sides of the rectangle be 5x and 4x. (Since, they are in the ratio 5 : 4)
Now, perimeter of rectangle = 2 (Length + Breadth)
72 = 2 (5x + 4x)
72 = 2 × 9x
72 = 18x
x = 4
Thus, the length of the rectangle = 5x = 5 × 4 = 20 cm
2. The cost of fencing a rectangular field 34 m long and 18 m wide at 2.25 per metre is
(a) Rs 243 (b) Rs 234 (c) Rs 240 (d) Rs 334
Answer: (b) Rs. 234
Explanation:
To fence the rectangular field, we need to find the perimeter of the rectangle.
Length of the rectangle = 34 m
Breadth of the rectangle = 18 m
Perimeter of the rectangle = 2 (Length + Breadth) = 2 (34 + 18) m = 2 × 52 m = 104 m
Cost of fencing the field at the rate of Rs. 2.25 per meter = Rs. 104 × 2.25 = Rs. 234
3. If the cost of fencing a rectangular field at Rs. 7.50 per metre is Rs. 600, and the length of the field is 24 m, then the breadth of the field is
(a) 8 m (b) 18 m (c) 24 m (d) 16 m
Answer: (d) 16 m
Explanation:
Cost of fencing the rectangular field = Rs. 600
Rate of fencing the field = Rs. 7.50 per m
Therefore, perimeter of the field = Cost of fencing / Rate of fencing = 600 / 7.50 = 80 m
Now, length of the field = 24 m
Therefore, breadth of the field = Perimeter / 2 – Length = 80 / 2- 24 = 16 m
4. The cost of putting a fence around a square field at 2.50 per metre is 200. The length of each side of the field is
(a) 80 m (b) 40 m (c) 20 m (d) None of these
Answer: (c) 20 m
Explanation:
Cost of fencing the square field = Rs. 200
Rate of fencing the field = Rs. 2.50
Now, perimeter of the square field = Cost of fencing / Rate of fencing = 200 / 2.50 = 80 m
Perimeter of square = 4 x Side of the square
Therefore, side of the square = Perimeter / 4 = 80 / 4 = 20 m
5. The length of a rectangle is three times of its width. If the length of the diagonal! is
(a)
Answer: (d) 64 m
Explanation:
Let us consider a rectangle ABCD.
Also, let us assume that the width of the rectangle, i.e., BC be x m.
It is given that the length is three times width of the rectangle.
Therefore, length of the rectangle, i.e., AB = 3x m
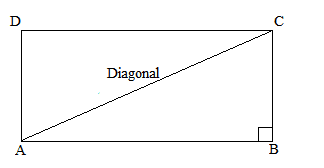
Now, AC is the diagonal of rectangle.
In right angled triangle ABC.
AC2 = AB2 + BC2
640 = 9x2 + x2
640 = 10x2
x2 = 640 / 10 = 64
x = 64 = 8 m
Thus, breadth of the rectangle = x = 8 m
Similarly, length of the rectangle = 3x = 3 x 8 = 24 m
Perimeter of the rectangle = 2 (Length + Breadth)
= 2 (24 + 8)
= 2 x 32 = 64 m
6. If a diagonal of a rectangle is thrice its smaller side, then its length and breadth are in the ratio
(a) 3 : 1 (b)
Answer: (d) 22 : 1
Explanation:
Let us assume that the length of the smaller side of the rectangle, i.e., BC be x and length of the larger side , i.e., AB be y.
It is given that the length of the diagonal is three times that of the smaller side.
Therefore, diagonal = 3x = AC
Now, applying Pythagoras theorem, we get:
(Diagonal)2 = (Smaller side)2 + (Larger side)2
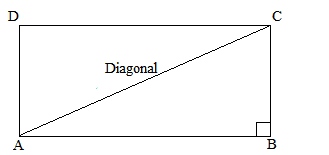
(AC)2 = (AB)2 + (BC)2
(3x)2 = (x)2 + (y)2
9x2 = x2 + y2
8x2 = y2
Now, taking square roots of both sides, we get:
22 x = y
or, y / x = 22 / 1
Thus, the ratio of the larger side to the smaller side = 22 : 1
7. The ratio of the areas of two squares, one having its diagonal double than the other, is
(a) 1 : 2 (b) 2:3 (c) 3 : 1 (d) 4 : 1
Answer: (d) 4 : 1
Explanation:
Let the two squares be ABCD and PQRS. Further, the diagonal of square PQRS is twice the diagonal of square ABCD

PR = 2 AC
Now, area of the square =
Area of PQRS =
Similarly, area of ABCD =
According to the question:
If AC = x units, then, PR = 2x units
Therefore, Area of PQRS / Area of ABCD =
Thus, the ratio of the areas of squares PQRS and ABCD = 4 : 1
8. If the ratio of areas of two squares is 225 : 256, then the ratio of their perimeters is
(a) 225 : 256 (b) 256 : 225 (c) 15:16 (d) 16 : 15
Answer: (c) 15 : 16
Explanation:
Let the two squares be ABCD and PQRS.
Further, let the lengths of each side of ABCD and PQRS be x and y, respectively.
Therefore Area of sq. ABCD / Area of sq. PQRS = x2 / y2
=> x2 / y2= 225 / 256
Taking square roots on both sides, we get:
x / y = 15 / 16
Now, the ratio of their perimeters:
Perimeter of sq. ABCD / Perimeter of sq. PQRS
= 4 × side of sq. ABCD / 4 × Side of sq. PQRS = 4x / 4y
Perimeter of sq. ABCD / Perimeter of sq. PQRS = x y
Perimeter of sq. ABCD / Perimeter of sq. PQRS = 15 / 16
Thus, the ratio of their perimeters = 15 : 16
9. If the sides of a square are halved, then its area
(a) remains same (b) becomes half (c) becomes one fourth
(d) becomes double
Answer: (c) becomes one fourth
Explanation:
Let the side of the square be x.
Then, area = (Side x Side) = (x × x) = x2
If the sides are halved, new side = x / 2
Now, new area =
=
It is clearly visible that the area has become one-fourth of its previous value.
10. A rectangular carpet has area 120 m2 and perimeter 46 metres. The length of its diagonal is
(a) 15 m (b) 16 m (c) 17 m (d) 20 m
Answer: (c) 17 m
Explanation:
Area of the rectangle = 120 m2
Perimeter = 46 m
Let the sides of the rectangle be l and b.
Therefore
Area = lb = 120 m2 …(1)
Perimeter = 2 (l + b) = 46
Or, (l + b) = 46 / 2 =23 m …(2)
Now, length of the diagonal of the rectangle = l2 + b2
So, we first find the value of (l2 + b2)
Using identity:
(l2 + b2) = (l + b)2 – 2 (lb) [From (1) and (2)]
Therefore
(l2 + b2) = (23)2 – 2 (120)
= 529 – 240 = 289
Thus, length of the diagonal of the rectangle = l2 + b2 = 289 = 17 m
11. If the ratio between the length and the perimeter of a rectangular plot is 1 : 3, then the ratio between the length and breadth of the plot is
(a) 1 : 2 (b) 2 : 1 (c) 3 : 2 (d) 2 : 3
Answer: (b) 2 : 1
Explanation:
It is given that Length of rectangle / Perimeter of rectangle = 1 / 3
=> l / (2l + 2b) = 1 / 3
After cross multiplying, we get:
3l = 2l + 2b
=> l = 2b
=> l / b= 2 / 1
Thus, the ratio of the length and the breadth is 2 : 1.
12. If the length of the diagonal of a square is 20 cm, then its perimeter is
(a)
Answer: (c)
Explanation:
Length of diagonal = 20 cm
Length of side of a square =
=
=
Therefore, perimeter of the square is 4 × Side = 4 ×
=
Comments