NCERT Solutions for Class 8 Maths Chapter 14, Exercise 14.3 is prepared according to the latest and updated syllabus pattern. These NCERT Solutions for Class 8 crafted by subject experts help students to follow a well-structured pattern of learning and score more. The best scores can be achieved in Maths subject by practising the textbook problems on a daily basis. The NCERT class 8 exercise solutions act as a great resource for practice and effective preparation for exams. Download now and start practising.

NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Exercise 14.3

Download PDF

carouselExampleControls112

Previous





Next

Access Other Exercise Solutions of Class 8 Maths Chapter 14 Factorisation

Exercise 14.1 Solutions: 3 Questions (Short answer type)
Exercise 14.2 Solutions: 5 Questions (Short answer type)
Exercise 14.4 Solutions: 21 Questions (Short answer type)

Access Answers to NCERT Class 8 Maths Chapter 14 Factorisation Exercise 14.3 Page number 227

1. Carry out the following divisions.

(i) 28x⁴ ÷ 56x

(ii) –36y³ ÷ 9y²

(iii) 66pq²r³ ÷ 11qr²

(iv) 34x³y³z³ ÷ 51xy²z³

(v) 12a⁸b⁸ ÷ (– 6a⁶b⁴)

Solution:

(i)28x⁴ = 2×2×7×x×x×x×x

56x = 2×2×2×7×x

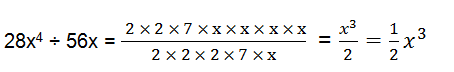
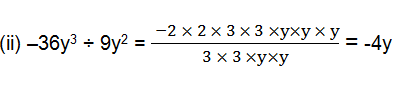
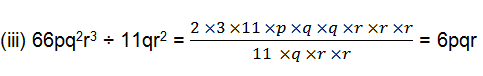
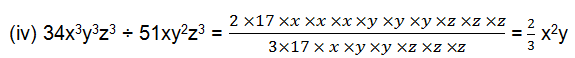
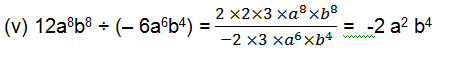
2. Divide the given polynomial by the given monomial.

(i)(5x²–6x) ÷ 3x

(ii)(3y⁸–4y⁶+5y⁴) ÷ y⁴

(iii) 8(x³y²z²+x²y³z²+x²y²z³)÷ 4x² y² z²

(iv)(x³+2x²+3x) ÷2x

(v) (p³q⁶–p⁶q³) ÷ p³q³

Solution:

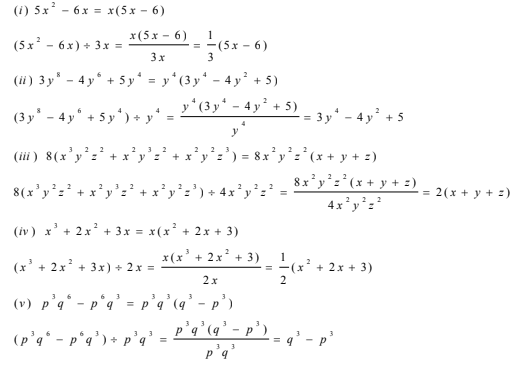
3. Work out the following divisions.

(i) (10x–25) ÷ 5

(ii) (10x–25) ÷ (2x–5)

(iii) 10y(6y+21) ÷ 5(2y+7)

(iv) 9x²y²(3z–24) ÷ 27xy(z–8)

(v) 96abc(3a–12)(5b–30) ÷ 144(a–4)(b–6)

Solution:

(i) (10x–25) ÷ 5 = 5(2x-5)/5 = 2x-5

(ii) (10x–25) ÷ (2x–5) = 5(2x-5)/( 2x-5) = 5

(iii) 10y(6y+21) ÷ 5(2y+7) = 10y×3(2y+7)/5(2y+7) = 6y

(iv) 9x²y²(3z–24) ÷ 27xy(z–8) = 9x²y²×3(z-8)/27xy(z-8) = xy

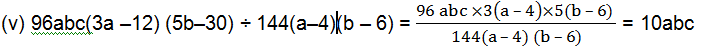
4. Divide as directed.

(i) 5(2x+1)(3x+5)÷ (2x+1)

(ii) 26xy(x+5)(y–4)÷13x(y–4)

(iii) 52pqr(p+q)(q+r)(r+p) ÷ 104pq(q+r)(r+p)

(iv) 20(y+4) (y²+5y+3) ÷ 5(y+4)

(v) x(x+1) (x+2)(x+3) ÷ x(x+1)

Solution:

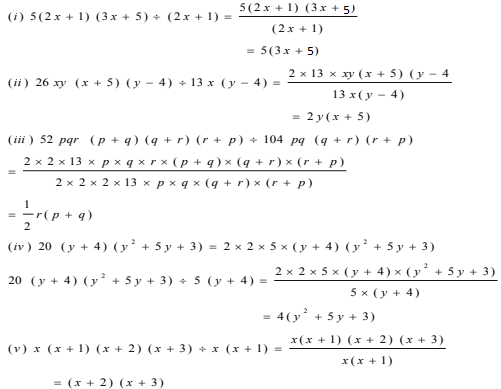
5. Factorise the expressions and divide them as directed.

(i) (y²+7y+10)÷(y+5)

(ii) (m²–14m–32)÷(m+2)

(iii) (5p²–25p+20)÷(p–1)

(iv) 4yz(z²+6z–16)÷2y(z+8)

(v) 5pq(p²–q²)÷2p(p+q)

(vi) 12xy(9x²–16y²)÷4xy(3x+4y)

(vii) 39y³(50y²–98) ÷ 26y²(5y+7)

Solution:

(i) (y²+7y+10)÷(y+5)

First, solve for equation (y²+7y+10)

(y²+7y+10) = y²+2y+5y+10 = y(y+2)+5(y+2) = (y+2)(y+5)

Now, (y²+7y+10)÷(y+5) = (y+2)(y+5)/(y+5) = y+2

(ii) (m²–14m–32)÷ (m+2)

Solving for m²–14m–32, we have

m²–14m–32 = m²+2m-16m–32 = m(m+2)–16(m+2) = (m–16)(m+2)

Now, (m²–14m–32)÷(m+2) = (m–16)(m+2)/(m+2) = m-16

(iii) (5p²–25p+20)÷(p–1)

Step 1: Take 5 common from the equation, 5p²–25p+20, we get

5p²–25p+20 = 5(p²–5p+4)

Step 2: Factorize p²–5p+4

p²–5p+4 = p²–p-4p+4 = (p–1)(p–4)

Step 3: Solve the original equation

(5p²–25p+20)÷(p–1) = 5(p–1)(p–4)/(p-1) = 5(p–4)

(iv) 4yz(z² + 6z–16)÷ 2y(z+8)

Factorize z²+6z–16,

z²+6z–16 = z²-2z+8z–16 = (z–2)(z+8)

Now, 4yz(z²+6z–16) ÷ 2y(z+8) = 4yz(z–2)(z+8)/2y(z+8) = 2z(z-2)

(v) 5pq(p²–q²) ÷ 2p(p+q)

p²–q² can be written as (p–q)(p+q) using identity.

5pq(p²–q²) ÷ 2p(p+q) = 5pq(p–q)(p+q)/2p(p+q) = 5q(p-q)/2

(vi) 12xy(9x²–16y²) ÷ 4xy(3x+4y)

Factorize 9x²–16y² , we have

9x²–16y² = (3x)²–(4y)² = (3x+4y)(3x-4y) using identity: p²–q² = (p–q)(p+q)

Now, 12xy(9x²–16y²) ÷ 4xy(3x+4y) = 12xy(3x+4y)(3x-4y) /4xy(3x+4y) = 3(3x-4y)

(vii) 39y³(50y²–98) ÷ 26y²(5y+7)
st solve for 50y²–98, we have

50y²–98 = 2(25y²–49) = 2((5y)²–7²) = 2(5y–7)(5y+7)

Now, 39y³(50y²–98) ÷ 26y²(5y+7) =

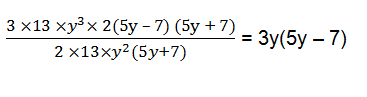
CBSE Class 8 Maths Chapter 14 Factorisation Exercise 14.3, is based on the topic of the division of algebraic expressions and subtopics like division of a monomial by another monomial, division of a polynomial by a monomial and division of algebraic expressions continued (Polynomial ÷ Polynomial). At the end of this section, students will get handy with the division of one algebraic expression by another and be able to solve such problems without any help.

Also, explore – 

NCERT Solutions for Class 8 Maths

NCERT Solutions for Class 8