RD Sharma Solutions for Class 9 Maths Chapter 4 – Free PDF Download
RD Sharma Solutions for Class 9 Maths Chapter 4 – Algebraic Identities are the most popular study materials among students. The answers to all the textbook questions are curated by subject experts at BYJU’S in a comprehensive manner. To enhance conceptual knowledge, students can follow these solutions designed by the experts in simple language. The algebraic equations, which are true for all values of variables in them, are called algebraic identities. RD Sharma Class 9 Solutions are helpful in obtaining an idea of important questions that might be asked in the final exam. Thorough practice of these solutions boosts time management and logical thinking abilities among students.
Students who aim to secure good marks in their final examinations can refer to RD Sharma Solutions. These solutions are formulated by the team of subject experts at BYJU’S to help students understand the covered concepts easily. Students who face difficulty in solving exercise-wise problems in the RD Sharma textbook can access solutions in a PDF format, both online and offline modes.
RD Sharma Solutions for Class 9 Maths Chapter 4 Algebraic Identities
Access Answers to Maths RD Sharma Solutions for Class 9 Chapter 4 Algebraic Identities
Exercise 4.1 Page No: 4.6
Question 1: Evaluate each of the following using identities:
(i) (2x – 1/x)2
(ii) (2x + y) (2x – y)
(iii) (a2b – b2a)2
(iv) (a – 0.1) (a + 0.1)
(v) (1.5.x2 – 0.3y2) (1.5x2 + 0.3y2)
Solution:
(i) (2x – 1/x)2
[Use identity: (a – b)2 = a2 + b2 – 2ab ]
(2x – 1/x)2 = (2x)2 + (1/x)2 – 2 (2x)(1/x)
= 4x2 + 1/x2 – 4
(ii) (2x + y) (2x – y)
[Use identity: (a – b)(a + b) = a2 – b2 ]
(2x + y) (2x – y) = (2x )2 – (y)2
= 4x2 – y2
(iii) (a2b – b2a)2
[Use identity: (a – b)2 = a2 + b2 – 2ab ]
(a2b – b2a)2 = (a2b) 2 + (b2a)2 – 2 (a2b)( b2a)
= a4b 2 + b4a2 – 2 a3b3
(iv) (a – 0.1) (a + 0.1)
[Use identity: (a – b)(a + b) = a2 – b2 ]
(a – 0.1) (a + 0.1) = (a)2 – (0.1)2
= (a)2 – 0.01
(v) (1.5 x2 – 0.3y2) (1.5 x2 + 0.3y2)
[Use identity: (a – b)(a + b) = a2 – b2 ]
(1.5 x2 – 0.3y2) (1.5x2 + 0.3y2) = (1.5 x2 ) 2 – (0.3y2)2
= 2.25 x4 – 0.09y4
Question 2: Evaluate each of the following using identities:
(i) (399)2
(ii) (0.98)2
(iii) 991 x 1009
(iv) 117 x 83
Solution:
(i)

(ii)

(iii)

(iv)

Question 3: Simplify each of the following:
(i) 175 x 175 +2 x 175 x 25 + 25 x 25
(ii) 322 x 322 – 2 x 322 x 22 + 22 x 22
(iii) 0.76 x 0.76 + 2 x 0.76 x 0.24 + 0.24 x 0.24
(iv)

Solution:
(i) 175 x 175 +2 x 175 x 25 + 25 x 25 = (175)2 + 2 (175) (25) + (25)2
= (175 + 25)2
[Because a2+ b2+2ab = (a+b)2 ]
= (200)2
= 40000
So, 175 x 175 +2 x 175 x 25 + 25 x 25 = 40000.
(ii) 322 x 322 – 2 x 322 x 22 + 22 x 22
= (322)2 – 2 x 322 x 22 + (22)2
= (322 – 22)2
[Because a2+ b2-2ab = (a-b)2]
= (300)2
= 90000
So, 322 x 322 – 2 x 322 x 22 + 22 x 22= 90000.
(iii) 0.76 x 0.76 + 2 x 0.76 x 0.24 + 0.24 x 0.24
= (0.76) 2 + 2 x 0.76 x 0.24 + (0.24) 2
= (0.76+0.24) 2
[ Because a2+ b2+2ab = (a+b)2]
= (1.00)2
= 1
So, 0.76 x 0.76 + 2 x 0.76 x 0.24 + 0.24 x 0.24 = 1.
(iv)

Question 4: If x + 1/x = 11, find the value of x2 +1/x2.
Solution:

Question 5: If x – 1/x = -1, find the value of x2 +1/x2.
Solution:
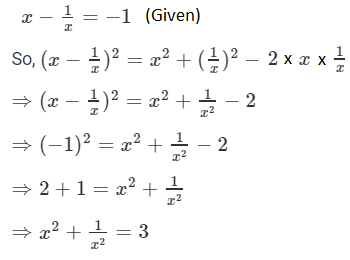
Exercise 4.2 Page No: 4.11
Question 1: Write the following in the expanded form:
(i) (a + 2b + c)2
(ii) (2a − 3b − c)2
(iii) (−3x+y+z)2
(iv) (m+2n−5p)2
(v) (2+x−2y)2
(vi) (a2 +b2 +c2) 2
(vii) (ab+bc+ca) 2
(viii) (x/y+y/z+z/x)2
(ix) (a/bc + b/ac + c/ab) 2
(x) (x+2y+4z) 2
(xi) (2x−y+z) 2
(xii) (−2x+3y+2z) 2
Solution:
Using identities:
(x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2xz
(i) (a + 2b + c)2
= a2 + (2b) 2 + c2 + 2a(2b) + 2ac + 2(2b)c
= a2 + 4b2 + c2 + 4ab + 2ac + 4bc
(ii) (2a − 3b − c)2
= [(2a) + (−3b) + (−c)]2
= (2a) 2 + (−3b) 2 + (−c) 2 + 2(2a)(−3b) + 2(−3b)(−c) + 2(2a)(−c)
= 4a2 + 9b2 + c2 − 12ab + 6bc − 4ca
(iii) (−3x+y+z)2
= [(−3x) 2 + y2 + z2 + 2(−3x)y + 2yz + 2(−3x)z
= 9x2 + y2 + z2 − 6xy + 2yz − 6xz
(iv) (m+2n−5p)2
= m2 + (2n) 2 + (−5p) 2 + 2m × 2n + (2×2n×−5p) + 2m × −5p
= m2 + 4n2 + 25p2 + 4mn − 20np − 10pm
(v) (2+x−2y)2
= 22 + x2 + (−2y) 2 + 2(2)(x) + 2(x)(−2y) + 2(2)(−2y)
= 4 + x2 + 4y2 + 4 x − 4xy − 8y
(vi) (a2 +b2 +c2) 2
= (a2) 2 + (b2) 2 + (c2 ) 2 + 2a2 b2 + 2b2c2 + 2a2c2
= a4 + b4 + c4 + 2a2 b2 + 2b2 c2 + 2c2 a2
(vii) (ab+bc+ca) 2
= (ab)2 + (bc) 2 + (ca) 2 + 2(ab)(bc) + 2(bc)(ca) + 2(ab)(ca)
= a2 b2 + b2c2 + c2 a2 + 2(ac)b2 + 2(ab)(c) 2 + 2(bc)(a) 2
(viii) (x/y+y/z+z/x)2

(ix) (a/bc + b/ac + c/ab) 2

(x) (x+2y+4z) 2
= x2 + (2y) 2 + (4z) 2 + (2x)(2y) + 2(2y)(4z) + 2x(4z)
= x2 + 4y2 + 16z2 + 4xy + 16yz + 8xz
(xi) (2x−y+z) 2
= (2x) 2 + (−y) 2 + (z) 2 + 2(2x)(−y) + 2(−y)(z) + 2(2x)(z)
= 4x2 + y2 + z2 − 4xy−2yz+4xz
(xii) (−2x+3y+2z) 2
= (−2x) 2 + (3y) 2 + ( 2z) 2 + 2(−2x)(3y)+2(3y)(2z)+2(−2x)(2z)
= 4x2 + 9y2 + 4z2 −12xy+12yz−8xz
Question 2: Simplify
(i) (a + b + c)2 + (a − b + c) 2
(ii) (a + b + c)2 − (a − b + c) 2
(iii) (a + b + c)2 + (a – b + c) 2 + (a + b − c) 2
(iv) (2x + p − c)2 − (2x − p + c) 2
(v) (x2 + y2 − z2) 2 − (x2 − y2 + z2) 2
Solution:
(i) (a + b + c)2 + (a − b + c) 2
= (a2 + b2 + c2 + 2ab+2bc+2ca) + (a2 + (−b) 2 + c2 −2ab−2bc+2ca)
= 2a2 + 2 b2 + 2c2 + 4ca
(ii) (a + b + c)2 − (a − b + c) 2
= (a2 + b2 + c2 + 2ab+2bc+2ca) − (a2 + (−b) 2 + c2 −2ab−2bc+2ca)
= a2 + b2 + c2 + 2ab + 2bc + 2ca − a2 − b2 − c2 + 2ab + 2bc − 2ca
= 4ab + 4bc
(iii) (a + b + c)2 + (a – b + c) 2 + (a + b − c) 2
= a2 + b2 + c2 + 2ab + 2bc + 2ca + (a2 + b2 + (c) 2 − 2ab − 2cb + 2ca) + (a2 + b2 + c2 + 2ab − 2bc – 2ca)
= 3 a2 + 3b2 + 3c2 + 2ab − 2bc + 2ca
(iv) (2x + p − c)2 − (2x − p + c) 2
= [4x2 + p2 + c2 + 4xp − 2pc − 4xc] − [4x2 + p2 + c2 − 4xp− 2pc + 4xc]
= 4x2 + p2 + c2 + 4xp − 2pc − 4cx − 4x2 − p2 − c2 + 4xp + 2pc− 4cx
= 8xp − 8xc
= 8(xp − xc)
(v) (x2 + y2 − z2) 2 − (x2 − y2 + z2) 2
= (x2 + y2 + (−z) 2) 2 − (x2 − y2 + z2) 2
= [x4 + y4 + z4 + 2x2y2 – 2y2z 2 – 2x2z2 − [x4 + y4 + z4 − 2x2y2 − 2y2z2 + 2x2z2]
= 4x2y2 – 4z2x2
Question 3: If a + b + c = 0 and a2 + b2 + c2 = 16, find the value of ab + bc + ca.
Solution:
a + b + c = 0 and a2 + b2 + c2 = 16 (given)
Choose a + b + c = 0
Squaring both sides,
(a + b + c)2 = 0
a2 + b2 + c2 + 2(ab + bc + ca) = 0
16 + 2(ab + bc + c) = 0
2(ab + bc + ca) = -16
ab + bc + ca = -16/2 = -8
or ab + bc + ca = -8
Exercise 4.3 Page No: 4.19
Question 1: Find the cube of each of the following binomial expressions:
(i) (1/x + y/3)
(ii) (3/x – 2/x2)
(iii) (2x + 3/x)
(iv) (4 – 1/3x)
Solution:
[Using identities: (a + b)3 = a3 + b3 + 3ab(a + b) and (a – b)3 = a3 – b3 – 3ab(a – b) ]
(i)

(ii)

(iii)

(iv)

Question 2: Simplify each of the following:
(i) (x + 3)3 + (x – 3) 3
(ii) (x/2 + y/3) 3 – (x/2 – y/3) 3
(iii) (x + 2/x) 3 + (x – 2/x) 3
(iv) (2x – 5y) 3 – (2x + 5y) 3
Solution:
[Using identities:a3 + b3 = (a + b)(a2 + b2 – ab)
a3 – b3 = (a – b)(a2 + b2 + ab)
(a + b)(a-b) = a2 – b2
(a + b)2 = a2 + b2 + 2ab and
(a – b)2 = a2 + b2 – 2ab]
(i) (x + 3)3 + (x – 3) 3
Here a = (x + 3), b = (x – 3)

(ii) (x/2 + y/3) 3 – (x/2 – y/3) 3
Here a = (x/2 + y/3) and b = (x/2 – y/3)

(iii) (x + 2/x) 3 + (x – 2/x) 3
Here a = (x + 2/x) and b = (x – 2/x)

(iv) (2x – 5y) 3 – (2x + 5y) 3
Here a = (2x – 5y) and b = 2x + 5y

Question 3: If a + b = 10 and ab = 21, find the value of a3 + b3.
Solution:
a + b = 10, ab = 21 (given)
Choose a + b = 10
Cubing both sides,
(a + b)3 = (10)3
a3 + b3 + 3ab(a + b) = 1000
a3 + b3 + 3 x 21 x 10 = 1000 (using given values)
a3 + b3 + 630 = 1000
a3 + b3 = 1000 – 630 = 370
or a3 + b3 = 370
Question 4: If a – b = 4 and ab = 21, find the value of a3 – b3.
Solution:
a – b = 4, ab= 21 (given)
Choose a – b = 4
Cubing both sides,
(a – b)3 = (4)3
a3 – b3 – 3ab (a – b) = 64
a3 – b3 – 3 × 21 x 4 = 64 (using given values)
a3 – b3 – 252 = 64
a3 – b3 = 64 + 252
= 316
Or a3 – b3 = 316
Question 5: If x + 1/x = 5, find the value of x3 + 1/x3 .
Solution:
Given: x + 1/x = 5
Apply Cube on x + 1/x

Question 6: If x – 1/x = 7, find the value of x3 – 1/x3 .
Solution:
Given: x – 1/x = 7
Apply Cube on x – 1/x

Question 7: If x – 1/x = 5, find the value of x3 – 1/x3 .
Solution:
Given: x – 1/x = 5
Apply Cube on x – 1/x
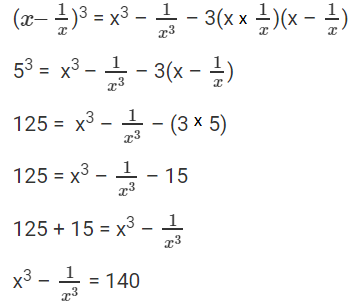
Question 8: If (x2 + 1/x2) = 51, find the value of x3 – 1/x3.
Solution:
We know that: (x – y)2 = x2 + y2 – 2xy
Replace y with 1/x, we get
(x – 1/x)2 = x2 + 1/x2 – 2
Since (x2 + 1/x2) = 51 (given)
(x – 1/x)2 = 51 – 2 = 49
or (x – 1/x) = ±7
Now, Find x3 – 1/x3
We know that, x3 – y3 = (x – y)(x2 + y2 + xy)
Replace y with 1/x, we get
x3 – 1/x3 = (x – 1/x)(x2 + 1/x2 + 1)
Use (x – 1/x) = 7 and (x2 + 1/x2) = 51
x3 – 1/x3 = 7 x 52 = 364
x3 – 1/x3 = 364
Question 9: If (x2 + 1/x2) = 98, find the value of x3 + 1/x3.
Solution:
We know that: (x + y)2 = x2 + y2 + 2xy
Replace y with 1/x, we get
(x + 1/x)2 = x2 + 1/x2 + 2
Since (x2 + 1/x2) = 98 (given)
(x + 1/x)2 = 98 + 2 = 100
or (x + 1/x) = ±10
Now, Find x3 + 1/x3
We know that, x3 + y3 = (x + y)(x2 + y2 – xy)
Replace y with 1/x, we get
x3 + 1/x3 = (x + 1/x)(x2 + 1/x2 – 1)
Use (x + 1/x) = 10 and (x2 + 1/x2) = 98
x3 + 1/x3 = 10 x 97 = 970
x3 + 1/x3 = 970
Question 10: If 2x + 3y = 13 and xy = 6, find the value of 8x3 + 27y3.
Solution:
Given: 2x + 3y = 13, xy = 6
Cubing 2x + 3y = 13 both sides, we get
(2x + 3y)3 = (13)3
(2x)3 + (3y) 3 + 3( 2x )(3y) (2x + 3y) = 2197
8x3 + 27y3 + 18xy(2x + 3y) = 2197
8x3 + 27y3 + 18 x 6 x 13 = 2197
8x3 + 27y3 + 1404 = 2197
8x3 + 27y3 = 2197 – 1404 = 793
8x3 + 27y3 = 793
Question 11: If 3x – 2y= 11 and xy = 12, find the value of 27x3 – 8y3.
Solution:
Given: 3x – 2y = 11 and xy = 12
Cubing 3x – 2y = 11 both sides, we get
(3x – 2y)3 = (11)3
(3x)3 – (2y)3 – 3 ( 3x)( 2y) (3x – 2y) =1331
27x3 – 8y3 – 18xy(3x -2y) =1331
27x3 – 8y3 – 18 x 12 x 11 = 1331
27x3 – 8y3 – 2376 = 1331
27x3 – 8y3 = 1331 + 2376 = 3707
27x3 – 8y3 = 3707
Exercise 4.4 Page No: 4.23
Question 1: Find the following products:
(i) (3x + 2y)(9x2 – 6xy + 4y2)
(ii) (4x – 5y)(16x2 + 20xy + 25y2)
(iii) (7p4 + q)(49p8 – 7p4q + q2)
(iv) (x/2 + 2y)(x2/4 – xy + 4y2)
(v) (3/x – 5/y)(9/x2 + 25/y2 + 15/xy)
(vi) (3 + 5/x)(9 – 15/x + 25/x2)
(vii) (2/x + 3x)(4/x2 + 9x2 – 6)
(viii) (3/x – 2x2)(9/x2 + 4x4 – 6x)
(ix) (1 – x)(1 + x + x2)
(x) (1 + x)(1 – x + x2)
(xi) (x2 – 1)(x4 + x2 +1)
(xii) (x3 + 1)(x6 – x3 + 1)
Solution:
(i) (3x + 2y)(9x2 – 6xy + 4y2)
= (3x + 2y)[(3x)2 – (3x)(2y) + (2y)2)]
We know, a3 + b3 = (a + b)(a2 + b2 – ab)
= (3x)3 + (2y) 3
= 27x3 + 8y3
(ii) (4x – 5y)(16x2 + 20xy + 25y2)
= (4x – 5y)[(4x)2 + (4x)(5y) + (5y)2)]
We know, a3 – b3 = (a – b)(a2 + b2 + ab)
= (4x)3 – (5y) 3
= 64x3 – 125y3
(iii) (7p4 + q)(49p8 – 7p4q + q2)
= (7p4 + q)[(7p4)2 – (7p4)(q) + (q)2)]
We know, a3 + b3 = (a + b)(a2 + b2 – ab)
= (7p4)3 + (q) 3
= 343 p12 + q3
(iv) (x/2 + 2y)(x2/4 – xy + 4y2)
We know, a3 – b3 = (a – b)(a2 + b2 + ab)
(x/2 + 2y)(x2/4 – xy + 4y2)

(v) (3/x – 5/y)(9/x2 + 25/y2 + 15/xy)

[Using a3 – b3 = (a – b)(a2 + b2 + ab) ]
(vi) (3 + 5/x)(9 – 15/x + 25/x2)

[Using: a3 + b3 = (a + b)(a2 + b2 – ab)]
(vii) (2/x + 3x)(4/x2 + 9x2 – 6)

[Using: a3 + b3 = (a + b)(a2 + b2 – ab)]
(viii) (3/x – 2x2)(9/x2 + 4x4 – 6x)

[Using : a3 – b3 = (a – b)(a2 + b2 + ab)]
(ix) (1 – x)(1 + x + x2)
And we know, a3 – b3 = (a – b)(a2 + b2 + ab)
(1 – x)(1 + x + x2) can be written as
(1 – x)[(12 + (1)(x)+ x2)]
= (1)3 – (x)3
= 1 – x3
(x) (1 + x)(1 – x + x2)
And we know, a3 + b3 = (a + b)(a2 + b2 – ab)]
(1 + x)(1 – x + x2) can be written as,
(1 + x)[(12 – (1)(x) + x2)]
= (1)3 + (x) 3
= 1 + x3
(xi) (x2 – 1)(x4 + x2 +1) can be written as,
(x2 – 1)[(x2)2 – 12 + (x2)(1)]
= (x2)3 – 13
= x6 – 1
[using a3 – b3 = (a – b)(a2 + b2 + ab) ]
(xii) (x3 + 1)(x6 – x3 + 1) can be written as,
(x3 + 1)[(x3)2 – (x3)(1) + 12]
= (x3) 3 + 13
= x9 + 1
[using a3 + b3 = (a + b)(a2 + b2 – ab) ]
Question 2: If x = 3 and y = -1, find the values of each of the following using in identity:
(i) (9y2 – 4x2)(81y4 + 36x2y2 + 16x4)
(ii) (3/x – x/3)(x2 /9 + 9/x2 + 1)
(iii) (x/7 + y/3)(x2/49 + y2/9 – xy/21)
(iv) (x/4 – y/3)(x2/16 + xy/12 + y2/9)
(v) (5/x + 5x)(25/x2 – 25 + 25x2)
Solution:
(i) (9y2 – 4x2)(81y4 + 36x2y2 + 16x4)
= (9y2 – 4x2) [(9y2 ) 2 + 9y2 x 4x2 + (4x2) 2 ]
= (9y2 ) 3 – (4x2)3
= 729 y6 – 64 x6
Put x = 3 and y = -1
= 729 – 46656
= – 45927
(ii) Put x = 3 and y = -1
(3/x – x/3)(x2 /9 + 9/x2 + 1)

(iii) Put x = 3 and y = -1
(x/7 + y/3)(x2/49 + y2/9 – xy/21)

(iv) Put x = 3 and y = -1
(x/4 – y/3)(x2/16 + xy/12 + y2/9)

(v) Put x = 3 and y = -1
(5/x + 5x)(25/x2 – 25 + 25x2)
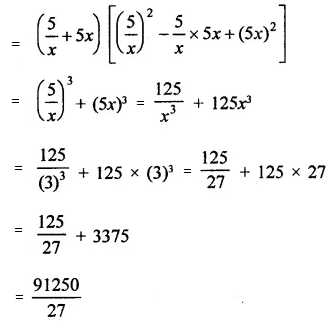
Question 3: If a + b = 10 and ab = 16, find the value of a2 – ab + b2 and a2 + ab + b2.
Solution:
a + b = 10, ab = 16
Squaring, a + b = 10, both sides
(a + b)2 = (10)2
a2 + b2 + 2ab = 100
a2 + b2 + 2 x 16 = 100
a2 + b2 + 32 = 100
a2 + b2 = 100 – 32 = 68
a2 + b2 = 68
Again, a2 – ab + b2 = a2 + b2 – ab = 68 – 16 = 52 and
a2 + ab + b2 = a2 + b2 + ab = 68 + 16 = 84
Question 4: If a + b = 8 and ab = 6, find the value of a3 + b3.
Solution:
a + b = 8, ab = 6
Cubing, a + b = 8, both sides, we get
(a + b)3 = (8)3
a3 + b3 + 3ab(a + b) = 512
a3 + b3 + 3 x 6 x 8 = 512
a3 + b3 + 144 = 512
a3 + b3 = 512 – 144 = 368
a3 + b3 = 368
Exercise 4.5 Page No: 4.28
Question 1: Find the following products:
(i) (3x + 2y + 2z) (9x2 + 4y2 + 4z2 – 6xy – 4yz – 6zx)
(ii) (4x – 3y + 2z) (16x2 + 9y2 + 4z2 + 12xy + 6yz – 8zx)
(iii) (2a – 3b – 2c) (4a2 + 9b2 + 4c2 + 6ab – 6bc + 4ca)
(iv) (3x -4y + 5z) (9x2 + 16y2 + 25z2 + 12xy- 15zx + 20yz)
Solution:
(i) (3x + 2y + 2z) (9x2 + 4y2 + 4z2 – 6xy – 4yz – 6zx)
= (3x + 2y + 2z) [(3x)2 + (2y) 2 + (2z) 2 – 3x x 2y – 2y x 2z – 2z x 3x]
= (3x)3 + (2y)3 + (2z)3 – 3 x 3x x 2y x 2z
= 27x3 + 8y3 + 8Z3 – 36xyz
(ii) (4x – 3y + 2z) (16x2 + 9y2 + 4z2 + 12xy + 6yz – 8zx)
= (4x -3y + 2z) [(4x)2 + (-3y) 2 + (2z) 2 – 4x x (-3y) – (-3y) x (2z) – (2z x 4x)]
= (4x) 3 + (-3y) 3 + (2z) 3 – 3 x 4x x (-3y) x (2z)
= 64x3 – 27y3 + 8z3 + 72xyz
(iii) (2a -3b- 2c) (4a2 + 9b2 + 4c2 + 6ab – 6bc + 4ca)
= (2a -3b- 2c) [(2a) 2 + (-3b) 2 + (-2c) 2 – 2a x (-3b) – (-3b) x (-2c) – (-2c) x 2a]
= (2a)3 + (-3b) 3 + (-2c) 3 -3x 2a x (-3 b) (-2c)
= 8a3 – 21b3 – 8c3 – 36abc
(iv) (3x – 4y + 5z) (9x2 + 16y2 + 25z2 + 12xy – 15zx + 20yz)
= [3x + (-4y) + 5z] [(3x) 2 + (-4y) 2 + (5z) 2 – 3x x (-4y) -(-4y) (5z) – 5z x 3x]
= (3x) 3 + (-4y) 3 + (5z) 3 – 3 x 3x x (-4y) (5z)
= 27x3 – 64y3 + 125z3 + 180xyz
Question 2: If x + y + z = 8 and xy + yz+ zx = 20, find the value of x3 + y3 + z3 – 3xyz.
Solution:
We know, x3 + y3 + z3 – 3xyz = (x + y + z) (x2 + y2 + z2 – xy – yz – zx)
Squaring, x + y + z = 8 both sides, we get
(x + y + z)2 = (8) 2
x2 + y2 + z2 + 2(xy + yz + zx) = 64
x2 + y2 + z2 + 2 x 20 = 64
x2 + y2 + z2 + 40 = 64
x2 + y2 + z2 = 24
Now,
x3 + y3 + z3 – 3xyz = (x + y + z) [x2 + y2 + z2 – (xy + yz + zx)]
= 8(24 – 20)
= 8 x 4
= 32
⇒ x3 + y3 + z3 – 3xyz = 32
Question 3: If a +b + c = 9 and ab + bc + ca = 26, find the value of a3 + b3 + c3 – 3abc.
Solution:
a + b + c = 9, ab + bc + ca = 26
Squaring, a + b + c = 9 both sides, we get
(a + b + c)2 = (9)2
a2 + b2 + c2 + 2 (ab + bc + ca) = 81
a2 + b2 + c2 + 2 x 26 = 81
a2 + b2 + c2 + 52 = 81
a2 + b2 + c2 = 29
Now, a3 + b3 + c3 – 3abc = (a + b + c) [(a2 + b2 + c2 – (ab + bc + ca)]
= 9[29 – 26]
= 9 x 3
= 27
⇒ a3 + b3 + c3 – 3abc = 27
Exercise VSAQs Page No: 4.28
Question 1: If x + 1/x = 3, then find the value of x2 + 1/x2.
Solution:
x + 1/x = 3
Squaring both sides, we have
(x + 1/x)2 = 32
x2 + 1/x2 + 2 = 9
x2 + 1/x2 = 9 – 2 = 7
Question 2: If x + 1/x = 3, then find the value of x^6 + 1/x^6.
Solution:
x + 1/x = 3
Squaring both sides, we have
(x + 1/x)2 = 32
x2 + 1/x2 + 2 = 9
x2 + 1/x2 = 9 – 2 = 7
x2 + 1/x2 = 7 …(1)
Cubing equation (1) both sides,

Question 3: If a + b = 7 and ab = 12, find the value of a2 + b2.
Solution:
a + b = 7, ab = 12
Squaring, a + b = 7, both sides,
(a + b) 2 = (7) 2
a2 + b2 + 2ab = 49
a2 + b2 + 2 x 12 = 49
a2 + b2 + 24 = 49
a2 + b2 = 25
Question 4: If a – b = 5 and ab = 12, find the value of a2 + b2.
Solution:
a – b = 5, ab = 12
Squaring, a – b = 5, both sides,
(a – b)2 = (5)2
a2 + b2 – 2ab = 25
a2 + b2 – 2 x 12 = 25
a2 + b2 – 24 = 25
a2 + b2 = 49
RD Sharma Solutions for Class 9 Maths Chapter 4 Algebraic Identities
In the 4th Chapter of Class 9 RD Sharma Solutions, students will study important identities, as listed below.
- Algebraic identities introduction
- Identity for the square of a trinomial
- Sum and difference of cubes identity
These books are widely used by students to score high in the final exam. For RD Sharma Class 9 Maths Solutions, students can visit BYJU’S website and access step-by-step answers to all the questions provided in the RD Sharma textbook.
Frequently Asked Questions on RD Sharma Solutions for Class 9 Maths Chapter 4
Write the key benefits of RD Sharma Solutions for Class 9 Maths Chapter 4.
1. The solutions provided in RD Sharma Solutions for Class 9 Maths Chapter 4 are offered in a step-by-step approach for a better understanding of concepts.
2. They also provide explanatory diagrams and tables for effective learning and conceptual clarity, which are crucial for the final exam.
3. These solutions help students to build a good knowledge of basics as well as advanced mathematical concepts.
4. Besides, they help students to understand the concepts in an effective manner.




























Comments