RD Sharma Solutions Class 9 Maths Chapter 4 Algebraic Identities Exercise 4.3

RD Sharma Solutions for Class 9 Maths Chapter 4 Exercise 4.3 are available here. This exercise is about the identity for the cube of a binomial. In this exercise, we shall extend the identity for the square of a binomial to the cube of a binomial. To score excellent marks in the examination, students are advised to solve all the questions listed in the RD Sharma Class 9. Students can download the Class 9 Maths Chapter 4 PDF from the below link.

RD Sharma Solutions for Class 9 Maths Chapter 4 Algebraic Identities Exercise 4.3

Download PDF

carouselExampleControls112

Previous Next

Access Answers to Maths RD Sharma Solutions for Class 9 Chapter 4 Algebraic Identities Exercise 4.3 Page Number 4.19

Exercise 4.3 Page No: 4.19

Question 1: Find the cube of each of the following binomial expressions:

(i) (1/x + y/3)

(ii) (3/x – 2/x²)

(iii) (2x + 3/x)

(iv) (4 – 1/3x)

Solution:

(i)

(ii)

(iii)

(iv)

Question 2: Simplify each of the following:

(i) (x + 3)³ + (x – 3) ³

(ii) (x/2 + y/3) ³ – (x/2 – y/3) ³

(iii) (x + 2/x) ³ + (x – 2/x) ³

(iv) (2x – 5y) ³ – (2x + 5y) ³

Solution:

a³ + b³ = (a + b)(a² + b² – ab)

a³ – b³ = (a – b)(a² + b² + ab)

(a + b)(a-b) = a² – b²

(a + b)² = a² + b² + 2ab and

(a – b)² = a² + b² – 2ab]

(i) (x + 3)³ + (x – 3) ³

Here a = (x + 3), b = (x – 3)

(ii) (x/2 + y/3) ³ – (x/2 – y/3) ³

Here a = (x/2 + y/3) and b = (x/2 – y/3)

(iii) (x + 2/x) ³ + (x – 2/x) ³

Here a = (x + 2/x) and b = (x – 2/x)

(iv) (2x – 5y) ³ – (2x + 5y) ³

Here a = (2x – 5y) and b = 2x + 5y

Question 3: If a + b = 10 and ab = 21, find the value of a³ + b³.

Solution:

a + b = 10, ab = 21 (given)

Choose a + b = 10

Cubing both sides,

(a + b)³ = (10)³

a³ + b³ + 3ab(a + b) = 1000

a³ + b³ + 3 x 21 x 10 = 1000 (using given values)

a³ + b³ + 630 = 1000

a³ + b³ = 1000 – 630 = 370

or a³ + b³ = 370

Question 4: If a – b = 4 and ab = 21, find the value of a³ – b³.

Solution:

a – b = 4, ab= 21 (given)

Choose a – b = 4

Cubing both sides,

(a – b)³ = (4)³

a³ – b³ – 3ab (a – b) = 64

a³ – b³ – 3 × 21 x 4 = 64 (using given values)

a³ – b³ – 252 = 64

a³ – b³ = 64 + 252

= 316

Or a³ – b³ = 316

Question 5: If x + 1/x = 5, find the value of x³ + 1/x³ .

Solution:

Given: x + 1/x = 5

Apply Cube on x + 1/x

Question 6: If x – 1/x = 7, find the value of x³ – 1/x³ .

Solution:

Given: x – 1/x = 7

Apply Cube on x – 1/x

Question 7: If x – 1/x = 5, find the value of x³ – 1/x³ .

Solution:

Given: x – 1/x = 5

Apply Cube on x – 1/x

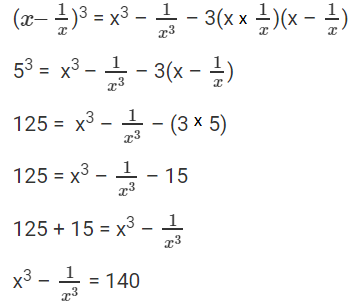
Question 8: If (x² + 1/x²) = 51, find the value of x³ – 1/x³.

Solution:

We know that: (x – y)² = x² + y² – 2xy

Replace y with 1/x, we get

(x – 1/x)² = x² + 1/x² – 2

Since (x² + 1/x²) = 51 (given)

(x – 1/x)² = 51 – 2 = 49

or (x – 1/x) = ±7

Now, Find x³ – 1/x³

We know that, x³ – y³ = (x – y)(x² + y² + xy)

Replace y with 1/x, we get

x³ – 1/x³ = (x – 1/x)(x² + 1/x² + 1)

Use (x – 1/x) = 7 and (x² + 1/x²) = 51

x³ – 1/x³ = 7 x 52 = 364

x³ – 1/x³ = 364

Question 9: If (x² + 1/x²) = 98, find the value of x³ + 1/x³.

Solution:

We know that: (x + y)² = x² + y² + 2xy

Replace y with 1/x, we get

(x + 1/x)² = x² + 1/x² + 2

Since (x² + 1/x²) = 98 (given)

(x + 1/x)² = 98 + 2 = 100

or (x + 1/x) = ±10

Now, Find x³ + 1/x³

We know that, x³ + y³ = (x + y)(x² + y² – xy)

Replace y with 1/x, we get

x³ + 1/x³ = (x + 1/x)(x² + 1/x² – 1)

Use (x + 1/x) = 10 and (x² + 1/x²) = 98

x³ + 1/x³ = 10 x 97 = 970

x³ + 1/x³ = 970

Question 10: If 2x + 3y = 13 and xy = 6, find the value of 8x³ + 27y³.

Solution:

Given: 2x + 3y = 13, xy = 6

Cubing 2x + 3y = 13 both sides, we get

(2x + 3y)³ = (13)³

(2x)³ + (3y) ³ + 3( 2x )(3y) (2x + 3y) = 2197

8x³ + 27y³ + 18xy(2x + 3y) = 2197

8x³ + 27y³ + 18 x 6 x 13 = 2197

8x³ + 27y³ + 1404 = 2197

8x³ + 27y³ = 2197 – 1404 = 793

8x³ + 27y³ = 793

Question 11: If 3x – 2y= 11 and xy = 12, find the value of 27x³ – 8y³.

Solution:

Given: 3x – 2y = 11 and xy = 12

Cubing 3x – 2y = 11 both sides, we get

(3x – 2y)³ = (11)³

(3x)³ – (2y)³ – 3 ( 3x)( 2y) (3x – 2y) =1331

27x³ – 8y³ – 18xy(3x -2y) =1331

27x³ – 8y³ – 18 x 12 x 11 = 1331

27x³ – 8y³ – 2376 = 1331

27x³ – 8y³ = 1331 + 2376 = 3707

27x³ – 8y³ = 3707

RD Sharma Solutions for Class 9 Maths Chapter 4 Algebraic Identities Exercise 4.3

RD Sharma Solutions for Class 9 Maths Chapter 4 Algebraic Identities Exercise 4.3 are based on the identity for the cube of a binomial.

Important properties:

• (a+b)³ = a³ + b³ + 3ab(a+b)
• (a – b)³ = a³ – b³ – 3ab(a – b)