NCERT Exemplar Solutions Class 11 Chemistry Chapter 6 – Free PDF Download
NCERT Exemplar Solutions for Class 11 Chemistry Chapter 6 Chemical Thermodynamics are important for the students who are preparing for the CBSE Class 11 examination and entrance exams like NEET, JEE and AIEEE. This page has answers to questions provided in the NCERT Exemplar book, along with extra questions prepared by subject experts at BYJU’S. NCERT Exemplar Class 11 Chapter 6 PDF has a variety of questions like MCQs, fill in the blanks, match the following, numerical problems, important derivations, HOTS, worksheets, and exercises which will assist you in understanding the topic from the perspective of examinations. Students can easily download these study materials and use them to learn the answers and get familiar with the type of questions that could be asked in the annual exam.
Thermodynamics is an important topic not just in Physics but also in Chemistry. It is also crucial for students to understand this topic clearly and develop a strong base, as it will be an integral part of their degree courses in future. Having said that, in NCERT Exemplar Class 11 Chemistry Chapter 6, students will learn the topic in the textbook, and they have to study a lot of concepts related to Thermodynamics. They will be learning about the interchange between heat and work, laws of thermodynamics, calorimetry, reaction enthalpy, etc. Thus, to help students quickly review and remember the essential concepts in Thermodynamics, NCERT Exemplar for Class 11 Chemistry Chapter 6 – Thermodynamics PDF is provided below.
Download the PDF of NCERT Exemplar Solutions for Class 11 Chemistry Chapter 6
Access Answers to NCERT Exemplar Solutions for Class 11 Chemistry Chapter 6
I. Multiple-choice Questions (Type-I)
1. Thermodynamics is not concerned about______.
(i) energy changes involved in a chemical reaction.
(ii) the extent to which a chemical reaction proceeds.
(iii) the rate at which a reaction proceeds.
(iv) the feasibility of a chemical reaction.
Solution:
Option (iii) is the answer.
2. Which of the following statements is correct?
(i) The presence of reacting species in a covered beaker is an example of
an open system.
(ii) There is an exchange of energy as well as a matter between the system
and the surroundings in a closed system.
(iii) The presence of reactants in a closed vessel made up of copper is an
example of a closed system.
(iv) The presence of reactants in a thermos flask or any other closed insulated
vessel is an example of a closed system.
Solution:
Option (iii) is the answer.
3. The state of a gas can be described by quoting the relationship between___.
(i) pressure, volume, temperature
(ii) temperature, amount, pressure
(iii) the amount, volume, temperature
(iv) pressure, volume, temperature, amount
Solution:
Option (iv) is the answer.
4. The volume of gas is reduced to half from its original volume. The specific
heat will be ______.
(i) reduce to half
(ii) be doubled
(iii) remain constant
(iv) increase four times
Solution:
Option (iii) is the answer.
5. During complete combustion of one mole of butane, 2658 kJ of heat is released.
The thermochemical reaction for above change is
(i) 2C4H10(g) + 13O2(g) → 8CO2(g) + 10H2O(l) ∆cH = –2658.0 kJ mol–1
(ii) C4H10(g) +13/2 O2 (g) → 4CO2 (g) + 5H2O (g) ∆cH = –1329.0 kJ mol–1
(iii) C4H10(g) +13/2 O2 (g) → 4CO2 (g) + 5H2O (l) ∆cH = –2658.0 kJ mol–1
(iv) C4H10 (g) +13/2 O2 (g) → 4CO2 (g) + 5H2O (l) ∆cH = +2658.0 kJ mol–1
Solution:
Option (iii) is the answer.
6. ∆fUᶱ of formation of CH4 (g) at a certain temperature is –393 kJ mol–1. The
value of ∆ fHᶱ is
(i) zero
(ii) < ∆f Uᶱ
(iii) > ∆f Uᶱ
(iv) equal to ∆f Uᶱ
Solution;
Option (ii) is the answer.
7. In an adiabatic process, no transfer of heat takes place between system and
surroundings. Choose the correct option for free expansion of an ideal gas
under adiabatic condition from the following.
(i) q = 0, ∆T ≠ 0, w = 0
(ii) q ≠ 0, ∆T = 0, w = 0
(iii) q = 0, ∆T = 0, w = 0
(iv) q = 0, ∆T < 0, w ≠ 0
Solution:
Option (iii) is the answer.
8. The pressure-volume work for an ideal gas can be calculated by using the expression w= ʃPexdv. The work can also be calculated from the pV– a plot by using the area under the curve within the specified limits. When an ideal gas is compressed (a) reversibly or (b) irreversibly from volume Vi
to Vf. choose the correct option.
(i) w (reversible) = w (irreversible)
(ii) w (reversible) < w (irreversible)
(iii) w (reversible) > w (irreversible)
(iv) w (reversible) = w (irreversible) + pex.∆V
Solution:
Option (ii) is the answer.
9. The entropy change can be calculated by using the expression ∆S = qrev/T
When water freezes in a glass beaker, choose the correct statement amongst
the following :
(i) ∆S (system) decreases but ∆S (surroundings) remains the same.
(ii) ∆S (system) increases but ∆S (surroundings) decreases.
(iii) ∆S (system) decreases but ∆S (surroundings) increases.
(iv) ∆S (system) decreases and ∆S (surroundings) also decreases.
Solution:
Option (iii) is the answer.
10. On the basis of thermochemical equations (a), (b) and (c), find out which of the
algebraic relationships given in options (i) to (iv) is correct.
(a) C (graphite) + O2 (g) → CO2 (g) ; ∆rH = x kJ mol–1
(b) C (graphite) +12 O2 (g) → CO (g) ; ∆rH = y kJ mol–1
(c) CO (g) +12 O2 (g) → CO2 (g) ; ∆rH = z kJ mol–1
(i) z = x + y
(ii) x = y – z
(iii) x = y + z
(iv) y = 2z – x
Solution:
Option (iii) is the answer.
11. Consider the reactions given below. On the basis of these reactions find out
which of the algebraic relations given in options (i) to (iv) is correct?
(a) C (g) + 4 H (g) → CH4 (g); ∆rH = x kJ mol–1
(b) C (graphite,s) + 2H2 (g) → CH4 (g); ∆rH = y kJ mol–1
(i) x = y
(ii) x = 2y
(iii) x > y
(iv) x < y
Solution:
Option (iii) is the answer.
12. The enthalpies of elements in their standard states are taken as zero. The
enthalpy of formation of a compound
(i) is always negative
(ii) is always positive
(iii) maybe positive or negative
(iv) is never negative
Solution:
Option (iii) is the answer.
13. Enthalpy of sublimation of a substance is equal to
(i) enthalpy of fusion + enthalpy of vapourisation
(ii) enthalpy of fusion
(iii) enthalpy of vapourisation
(iv) twice the enthalpy of vapourisation
Solution:
Option (i) is the answer.
14. Which of the following is not correct?
(i) ∆G is zero for a reversible reaction
(ii) ∆G is positive for a spontaneous reaction
(iii) ∆G is negative for a spontaneous reaction
(iv) ∆G is positive for a non-spontaneous reaction
Solution:
Option (ii) is the answer.
II. Multiple Choice Questions (Type-II)
In the following questions, two or more options may be correct.
15. Thermodynamics mainly deals with
(i) interrelation of various forms of energy and their transformation from
one form to another.
(ii) energy changes in the processes which depend only on initial and final
states of the microscopic systems containing a few molecules.
(iii) how and at what rate these energy transformations are carried out?
(iv) the system in an equilibrium state or moving from one equilibrium state to
another equilibrium state.
Solution:
Option (i) and (iv) are the answers.
16. In an exothermic reaction, heat is evolved, and the system loses heat to the
surrounding. For such a system
(i) qp will be negative
(ii) ∆rH will be negative
(iii) qp will be positive
(iv) ∆rH will be positive
Solution:
Option (i) and (ii) are the answers.
17. Spontaneity means having the potential to proceed without the assistance
of an external agency. The processes which occur spontaneously are
(i) flow of heat from colder to warmer body.
(ii) gas in a container contracting into one corner.
(iii) gas expanding to fill the available volume.
(iv) burning carbon in oxygen to give carbon dioxide.
Solution:
Option (iii) and (iv) are the answers.
18. For an ideal gas, the work of reversible expansion under isothermal condition
can be calculated by using the expression w = – nRT ln Vf/Vi
A sample containing 1.0 mol of an ideal gas is expanded isothermally and
reversibly to ten times of its original volume, in two separate experiments.
The expansion is carried out at 300 K and 600 K, respectively. Choose the
correct option.
(i) Work done at 600 K is 20 times the work done at 300 K.
(ii) Work done at 300 K is twice the work done at 600 K.
(iii) Work done at 600 K is twice the work done at 300 K.
(iv) ∆U = 0 in both cases.
Solution:
Option (iii) and (iv) are the answers.
19. Consider the following reaction between zinc and oxygen and choose the correct
options out of the options given below :
2 Zn (s) + O2 (g) → 2 ZnO (s) ; ∆H = – 693.8 kJ mol–1(i) The enthalpy of two moles of ZnO is less than the total enthalpy of two
moles of Zn and one mole of oxygen by 693.8 kJ.
(ii) The enthalpy of two moles of ZnO is more than the total enthalpy of two
moles of Zn and one mole of oxygen by 693.8 kJ.
(iii) 693.8 kJ mol–1 energy is evolved in the reaction.
(iv) 693.8 kJ mol–1 energy is absorbed in the reaction.
Solution:
Option (i) and (iii) are the answers.
III. Short Answer Type
20. 18.0 g of water completely vapourises at 100°C and 1 bar pressure and the enthalpy change in the process is 40.79 kJ mol–1. What will be the enthalpy change for vapourising two moles of water under the same conditions? What is the standard enthalpy of vapourisation for water?
Solution:
Enthalpy change of vapourisation for 1 mole = 40.79 kJ mol–1 enthalpy change of vapourisation for 2 moles of water = (40.79 × 2) = 81.58kJ mol–1
for water ∆Hvapourisation, ⁰ will be equal to =40.79 kJ mol–1
21. One mole of acetone requires less heat to vaporise than 1 mol of water. Which of the two liquids has a higher enthalpy of vapourisation?
Solution:
Among the two liquids, water has a higher enthalpy of vapourisation (consuming higher heat energy).
Therefore, ∆Hvapourisation (water) > ∆Hvapourisation (acetone).
22. Standard molar enthalpy of formation, Δf HΘis just a special case of enthalpy of reaction, Δr HΘ. Is the Δr HΘfor the following reaction the same as Δf HΘ? Give the reason for your answer.
CaO(s) + CO2(g) → CaCO3(s) ; ΔfHΘ = –178.3 kJ mol–1
Solution:
The given reaction CaO(s) + CO2(g) →CaCO3(s) indicates that it is occurring in the standard form of 1 mole of each substance. And the molar enthalpy of formation ΔfHΘ = –178.3 kJ mol–1 Given for CaCO3 is also showing the standard conditions.
So,ΔfHΘ = –178.3 kJ mol–1 = Δr HΘ .
23. The value of ΔfHΘfor NH3 is – 91.8 kJ mol–1. Calculate the enthalpy change for the following reaction :
2NH3(g) → N2(g) + 3H2(g)
Solution:
Enthalpy change of a reaction is calculated as
: Σbond enthalpy of reactants- Σbond enthalpy of products
for the decomposition 2NH3(g) →N2(g) + 3H2(g) ΔrHΘ will be =
– (– 91.8 kJ mol–1 ) = + 91.8 kJ mol–1
for 2 moles of NH3 enthalpy change of the reaction will be ΔrH = (2 X 91.8 ) = 183.6 kJ mol–1 .
24. Enthalpy is an extensive property. In general, if the enthalpy of an overall reaction A→B along one route is Δr H and Δr H1, ΔrH2, ΔrH3 ….. represent enthalpies of intermediate reactions leading to product B. What will be the relation between ΔrH for overall reaction and ΔrH1, ΔrH2….. etc. for intermediate reactions.
Solution:
For the reaction, A→B the formation of B goes through several intermediate reactions with different enthalpy values Δr H1, ΔrH2, ΔrH3….., and the overall enthalpy change is Δr H.
25. The enthalpy of atomisation for the reaction CH4(g)→ C(g) + 4H (g) is 1665 kJ mol–1. What is the bond energy of the C–H bond?
Solution:
For 1 C-H bond, the bond energy will be equal to 1/4 that of the enthalpy of atomisation
= (1665/4) = 416.25 kJ mol–1.
26. Use the following data to calculate Δlattice HΘfor NaBr.
Δsub HΘfor sodium metal = 108.4 kJ mol–1
Ionization enthalpy of sodium = 496 kJ mol–1
Electron gain enthalpy of bromine = – 325 kJ mol–1
Bond dissociation enthalpy of bromine = 192 kJ mol–1
Δf HΘfor NaBr (s) = – 360.1 kJ mol–1
Solution:
Sublimation of the metal(ΔsubHΘ) →Ionization of the metal (ΔiHΘ) →Dissociation of the non-metal (ΔdissHΘ) →Gain of electrons by the non-metal(ΔegHΘ)
Δf HΘ =Δsub HΘ+Δi HΘ+1/2 dissHΘ + ΔegHΘ+ ΔlattticeHΘ
To calculate the lattice enthalpy of NaBr,
Na(s) → Na(g) ; ΔsubHΘ =108.4 kJ mol–1 (i)
Na→ Na+ + e- ; ΔiHΘ = 496 kJ mol–1 (ii)
1/2 Br2→ Br ; 1/2 ΔdissHΘ = ( ) = 96 kJ mol–1 (iii)
Br + e-→ Br- ;ΔegHΘ= – 325 kJ mol–1 (iv)
enthalpy of formation Δf HΘ = processes (i) + (ii) + (ii) + (iv)
Δlattice HΘ = Δf HΘ – ΔsubHΘ – ΔiHΘ – 1/2 ΔdissHΘ –ΔegHΘ
= -735.5kjmol-1.
27. Given that ΔH = 0 for mixing of two gases. Explain whether the diffusion of these gases into each other in a closed container is a spontaneous process or not.
Solution:
A negative ∆G means the reaction will be the spontaneous included contribution of the other factors like enthalpy(H) and entropy(S).
∆G= ∆H – T∆S
∆H being 0,
∆G will be negative (as the positive value of ∆S will give a more negative T∆S)
∆H=0 ; ∆G= -T∆S= negative.
28. Heat has a randomising influence on a system, and temperature is the measure of the average chaotic motion of particles in the system. Write the mathematical relation which relates these three parameters.
Solution:
The mathematical relation which relates these three parameters is ΔS = qrev/T
where ΔS is the change in entropy and T stands for temperature.
29. Increase in enthalpy of the surroundings is equal to the decrease in enthalpy of the system. Will the temperature of the system and surroundings be the same when they are in thermal equilibrium?
Solution:
As thermal equilibrium obeys the zeroth law of thermodynamics, temperature of system and surroundings will be the same when they are in thermal equilibrium.
30. As thermal equilibrium obeys the zeroth law of thermodynamics, temperature of system and surroundings will be the same when they are in thermal equilibrium.
Solution:
For the given reaction N2O4 (g) ⇋2NO2 (g) the value of Kp = 0.98.
Hence, ∆rG⁰ = – RT ln(0.98)
Since ln(0.98) has a negative value, the value of ∆rG⁰ becomes positive. Therefore, the reaction is non-spontaneous.
31. A sample of 1.0 mol of a monoatomic ideal gas is taken through a cyclic
process of expansion and compression as shown in Fig. 6.1. What will be the
value of ∆H for the cycle as a whole?

Solution:
In the following cyclic ( 1 → 2 →3 →1 ) process the initial and final point is the same (i.e. 1). Hence the enthalpy change or ∆H= 0, in other words, there will be no change in enthalpy.
32. The standard molar entropy of H2O (l ) is 70 J K–1 mol–1. Will the standard molar entropy of H2O(s) be more or less than 70 J K–1 mol–1?
Solution:
The entropy of H2O(s) <entropy of H2O (l ). The standard molar entropy of H2O(s) will also be less than 70 J K–1 mol–1.
33. Identify the state functions and path functions out of the following :
enthalpy, entropy, heat, temperature, work, and free energy.
Solution:
State functions: enthalpy, entropy, temperature and free energy.
Path functions: Heat and work
34. The molar enthalpy of vapourisation of acetone is less than that of water. Why?
Solution:
Water has strong hydrogen bonds and the high polarity also adds up, resulting in it boiling at higher temperatures. Hence water has a higher molar enthalpy than acetone.
35. Which quantity out of ΔrG and ΔrGΘwill be zero at equilibrium?
Solution:
At equilibrium ΔrGΘ = – RT lnK .
ΔrGΘ can only be 0 when the value of K is =1. So, for all the other K values ΔrGΘ cannot be zero.
36. Predict the change in internal energy for an isolated system at constant volume.
Solution:
For an isolated system q=0 and w=0
And according to 1st law of thermodynamics: ∆U= q + w (U=internal energy)
Therefore, change in internal energy for an isolated system ∆U = 0.
37. Although heat is a path function but heats absorbed by the system under certain specific conditions is independent of path. What are those conditions? Explain.
Solution;
Heat is independent of the path under 2 conditions:
1. When the volume of the system is kept constant-
By 1st law of thermodynamics:
q = ΔU + (-w)
and -w = pΔV
Therefore , q = ΔU + pΔV
ΔV = 0 (at constant volume)
Hence, qv = ΔU + 0 = ΔU= change in internal energy
2. When the pressure of the system is kept constant –
At constant pressure, qp= ΔU + pΔV
But , ΔU + pΔV = ∆H
Therefore, qp = ∆H = change in enthalpy.
38. Expansion of gas in a vacuum is called free expansion. Calculate the work is done and the change in internal energy when 1 litre of an ideal gas expands isothermally into a vacuum until its total volume is 5 litre.
Solution:
Work done in vacuum is calculated by :
-w = Text (Vinitial – Vfinal )
Pext= 0
–w = 0x(5-1) = 0.
For isothermal expansion q=o
q= ∆U + (-w)
Hence ∆U will be 0.
39. Heat capacity (Cp) is an extensive property but specific heat (c) is an intensive property. What will be the relation between Cp and c for 1 mol of water?
Solution;
1 mole of water = 18 g.
Hence, for water, Heat capacity = 18 × specific heat.
i.e. Cp = 18 × C .
40. The difference between CP and CV can be derived using the empirical relation H = U + PV. Calculate the difference between CP and CV for 10 moles of an ideal gas.
Solution:
For an ideal gas, the difference between these two is CP – CV = nR, the universal gas constant and where n= no. of moles
Hence for 10 moles of an ideal gas CP – CV = 10 R
CP – CV = 10 × 8.314 J
= 83.14 J
41. If the combustion of 1g of graphite produces 20.7 kJ of heat, what will be molar enthalpy change? Give the significance of the sign also.
Solution:
The heat of combustion ∆Hc of graphite (i.e. carbon) is given as = 20.7 kJ for 1g of graphite (C).
1 mole of Carbon = 12 g
Hence the molar enthalpy change (enthalpy for 1 mole )
= (20.7 × 12 )= 248.4 KJ mol-1
Since the heat is evolved, the actual molar enthalpy change
= -248.4 KJ mol-1
In combustion reactions, heat is always evolved i.e. it is an exothermic reaction. Hence the sign of ∆H for the reaction will always be negative (for the process to occur).
42. The net enthalpy change of a reaction is the amount of energy required to break all the bonds in reactant molecules minus the amount of energy required to form all the bonds in the product molecules. What will be the enthalpy change for the following reaction?
H2(g) + Br2(g) → 2HBr(g)
Given that Bond energy of H2, Br2 and HBr is 435 kJ mol–1, 192 kJ mol–1 and 368 kJ mol–1 respectively.
Solution:
For the reaction
H2(g) + Br2(g) →2HBr(g)
Enthalpy change
= (Bond energy of H-H bond + Br-Br bond) – (2 × bond energy of H-Br)
= (435 + 192) kJ mol–1 – (2 × 368) kJ mol–1
= -109 kJ mol–1
43. The enthalpy of vapourisation of CCl4 is 30.5 kJ mol–1. Calculate the heat required for the vapourisation of 284 g of CCl4 at constant pressure. (Molar mass of CCl4 = 154 g mol–1).
Solution:
The enthalpy of vapourisation is given for 1 mole of CCl4 = 30.5 kJ mol–1
Hence, for 284 g, it will be = (mole no. × 30.5) kJ
Molar mass of CCl4 = 154 g mol–1 that means 154 g = 1 mole.
Therefore , 284 g = (284g/154gmol-1)= 1.84 mole.
Hence the heat required for the vapourisation of 284 g of CCl4 at constant pressure = (1.84 mol ×30.5 KJ mol-1) kJ
=56.12 KJ
44. The enthalpy of reaction for the reaction :
2H2(g) + O2(g) → 2H2O(l) is ∆HrΘ = – 572 kJ mol–1
What will be standard enthalpy of formation of H2O (l)?
Solution:
For the given reaction : 2H2(g) + O2(g) →2H2O(l)
the standard enthalpy of reaction is ∆HrΘ = – 572 kJ mol–1 , so the half of ∆HrΘ will be the standard molar enthalpy of formation ;
ΔfHΘ = 1/2 × ∆HrΘ = (-572/2) = -286 kJ mol–1 .
45. What will be the work done on an ideal gas enclosed in a cylinder, when it is compressed by constant external pressure, pext in a single step as shown in Fig? 6.2. Explain graphically.

Solution:
From this graph, we can obtain the be the work done on the ideal gas enclosed in the cylinder in 1 step: the area covered by P-V graph (shaded region) is the actual value of the work done is:
= length × breadth = pext ∆V = AVI (or BVII ) × (VI – VII )
46. How will you calculate work done on an ideal gas in a compression, when a change in pressure is carried out in infinite steps?
Solution:
When an ideal gas in a compression, where the change in pressure is carried out in infinite steps i.e. through a reversible process, the work done can be calculated only through the observation of pressure vs volume plot of the process.

The shaded area in the above graph represents the work done in the process, by calculating the area covered we can calculate the work done.
47. Represent the potential energy/enthalpy change in
the following processes graphically.
(a) Throwing a stone from the ground to the roof.
(b) 1/2 H2(g) + 1/2 Cl2(g) ⇋ HCl(g) ΔrHΘ = –92.32 kJ mol–1
In which of the processes potential energy/enthalpy change is contributing factor to the spontaneity?
Solution:
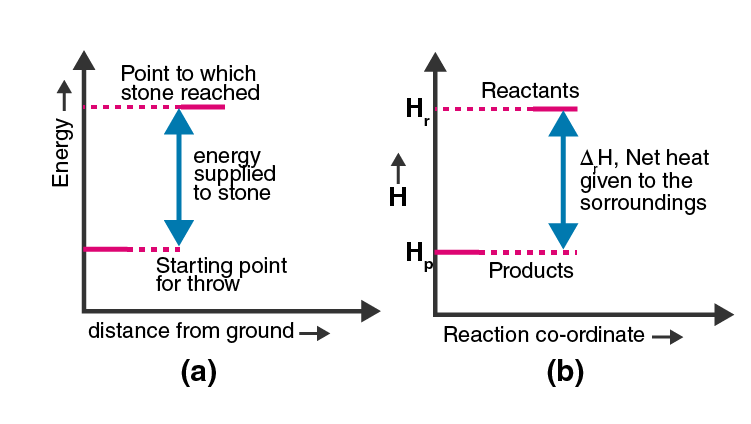
Amongst these two processes, in the process or reaction (b) the potential energy/enthalpy change is contributing factor to the spontaneity.
48. Enthalpy diagram for a particular reaction is given in Fig. 6.3. Is it possible to decide the spontaneity of a reaction from the given diagram? Explain.

Solution:
From the given enthalpy diagram, it can be said the change in enthalpy ∆H is positive for the reaction, i.e. it will be endothermic. But when it comes to the spontaneity of a reaction, enthalpy is just a factor and there are other important factors like entropy, Gibb’s free energy also taken into consideration. Hence enthalpy alone cannot determine the spontaneity of a reaction; one must have a loo to the other contributing factors also.
49. 1.0 mol of a monoatomic ideal gas is expanded from state (1) to state (2) as shown in Fig. 6.4. Calculate the work done for the expansion of gas from state (1) to state (2) at 298 K.
Solution:

W= – 2.303nRT log (p1/p2)
= – 2.303 × 1 mol × 8.314 J mol-1 K-1 × 298 K × log2
=- 2.303 × 8.314 × 298 × 0.3010 J
= -1717.46 J
50. An ideal gas is allowed to expand against a constant pressure of 2 bar from 10 L to 50 L in one step. Calculate the amount of work done by the gas. If the same expansion were carried out reversibly, will the work is done be higher or lower than the earlier case? (Given that 1 L bar = 100J)
Solution:
Amount of work done = -pext ∆V
= – 2 bar × (50 – 10 ) L = – 80 L bar.
Now, it is given that 1 L bar = 100 J
So , -80 L bar = (-80 × 100) = -8000 J
= -8 KJ is the amount of work done in the above process.
If it is reversible, then the internal pressure will be larger than the external pressure. So the work done will own a higher value.
Subtopics Covered in Class 11 Chemistry Chapter 6 Thermodynamics
- Thermodynamic Terms
- The System and the Surroundings
- Types of the System
- The State of the System
- Internal Energy as a State Function
- Applications
- Work
- Enthalpy, H
- Measurement of Du and Dh: Calorimetry
- Enthalpy Change, Drh of a Reaction – Reaction Enthalpy
- Enthalpies for Different Types of Reactions
- Spontaneity
- Gibbs Energy Change and Equilibrium.
Chapter 6, Thermodynamics, is one of the important chapters in Class 11 Chemistry that lays a strong foundation for all your future endeavours. It is very essential to grasp the Thermodynamics concept thoroughly to avoid difficulty in higher studies. In order to make students learn Chemistry topics easily, BYJU’S provides special videos, animations, and exercises that will not only help students understand the topic but also help in memorising the topic for a long period of time.
Frequently Asked Questions on NCERT Exemplar Solutions for Class 11 Chemistry Chapter 6
Why should I choose BYJU’S NCERT Exemplar Solutions for Class 11 Chemistry Chapter 6?
What can I learn in Chapter 6 of NCERT Exemplar Solutions for Class 11 Chemistry?
List out the topics/subtopics covered in Chapter 6 of NCERT Exemplar Solutions for Class 11 Chemistry.
1. Thermodynamic Terms
a. The System and the Surroundings
b. Types of the System
c. The State of the System
d. Internal Energy as a State Function
2. Applications
a. Work
b. Enthalpy
3. Measurement of Du and Dh: Calorimetry
4. Enthalpy Change, Drh of a Reaction – Reaction Enthalpy
5. Enthalpies for Different Types of Reactions
6. Spontaneity
7. Gibbs Energy Change and Equilibrium
| Also Access |
| NCERT Solutions for Class 11 Chemistry Chapter 6 |
| CBSE Notes for Class 11 Chemistry Chapter 6 |














Comments